Bottomhole Pressure Calculations

Estimating bottomhole pressure from measured wellhead pressure and temperature is an important task in petroleum engineering. Bottomhole pressures are required in most classical well-performance forecasting techniques such as rate-transient analysis (RTA), history matching using reservoir simulation, inflow-performance-relationship (IPR) estimation, and more.

Based on production data measured at the surface (i.e. surface rates, wellhead pressure, and wellhead temperature), and key properties describing the wellbore (i.e. a deviation survey describing the curvilinear shape of the well, wellbore diameter, and pipe roughness), we can estimate the bottomhole pressure by numerical integration of the pressure- and temperature gradient expression.

Multiphase flow in inclined pipe involves calculations of oil, gas, and water which require and accurate fluid description (PVT). We achieve this by leveraging all the relevant capabilities of whitson⁺ seemlessly to provide accurate and consistent phase behavior in all calculations made on a particular well.

Currently Supported Correlations:

• Hagedorn and Brown (Liquid-Rich Wells)
• Beggs and Brill (Liquid-Rich Wells)
• Gray (Low-LGR Gas Wells)
• Woldesemayat and Ghajar (Liquid-Rich Wells)

1. Input

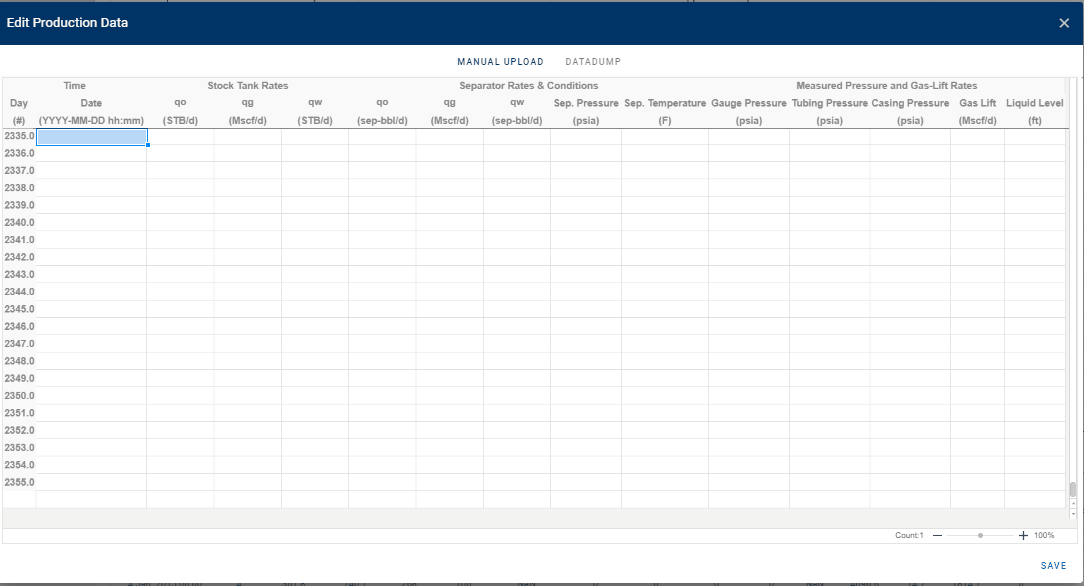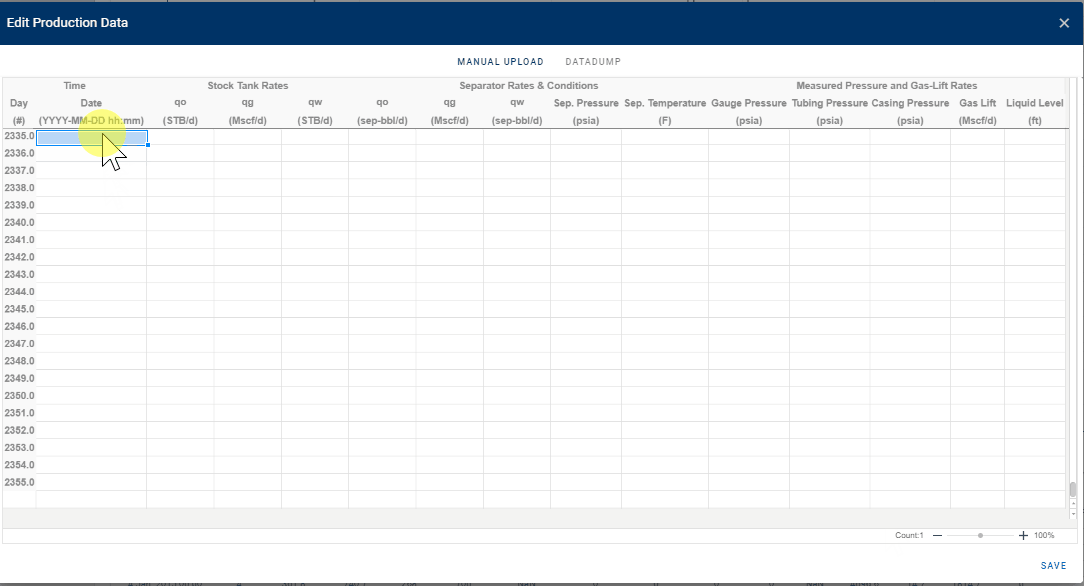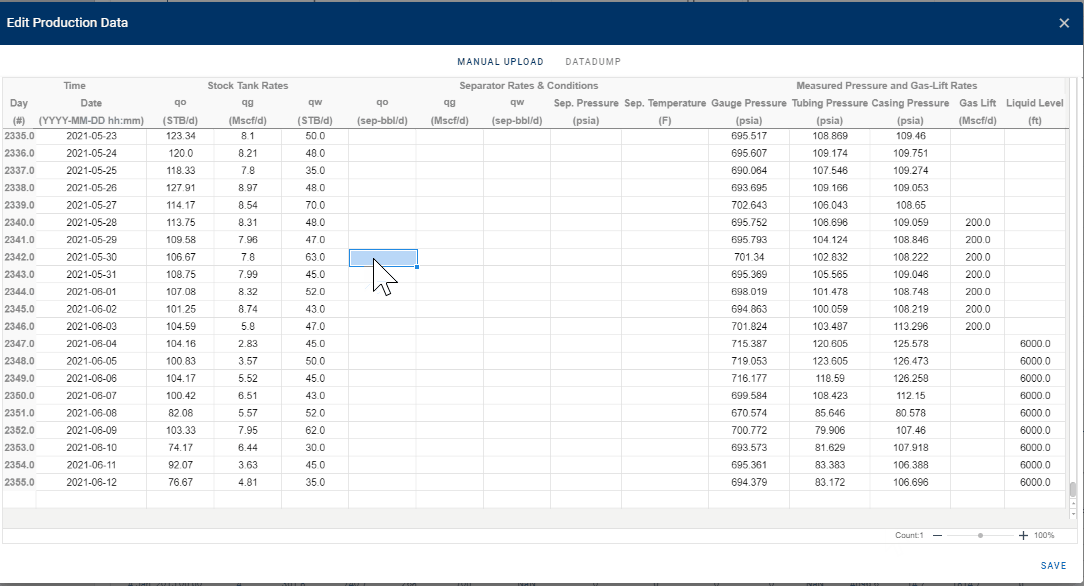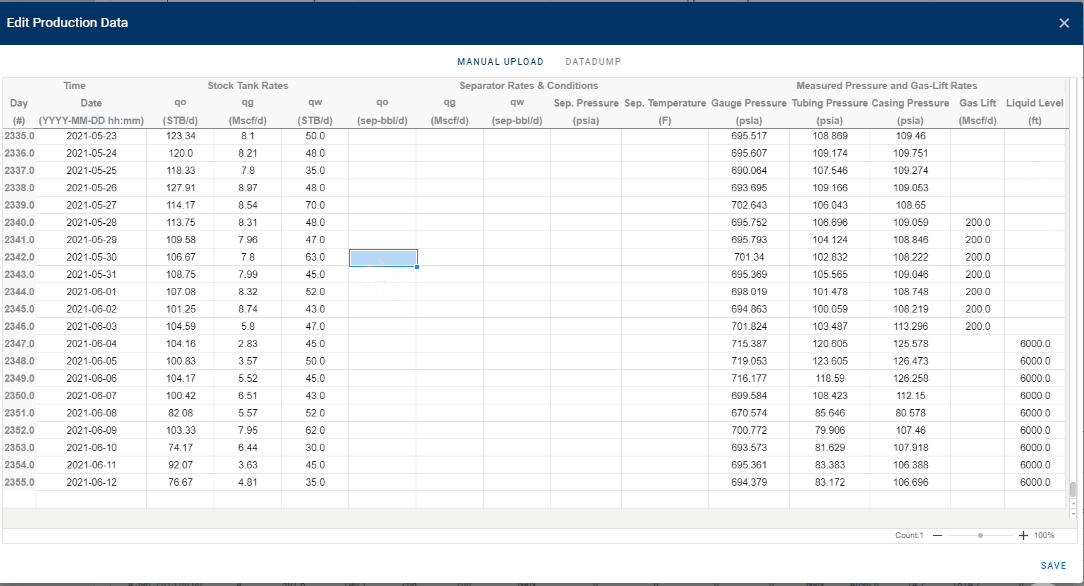
1.1 Production data

Daily production rates can be provided at stock-tank conditions or at separator conditions. If separator rates are provided, then the Common Process Conversion module can be used to generate stock-tank rates for the BHP calculations. In addition to production rates, one must also provide casinghead pressure and tubinghead pressure if a tubing is installed. If the well is subjected to either gas-lift or rod-pump assisted lift, lift-gas rates or liquid level in the annulus must be provided, respectively.

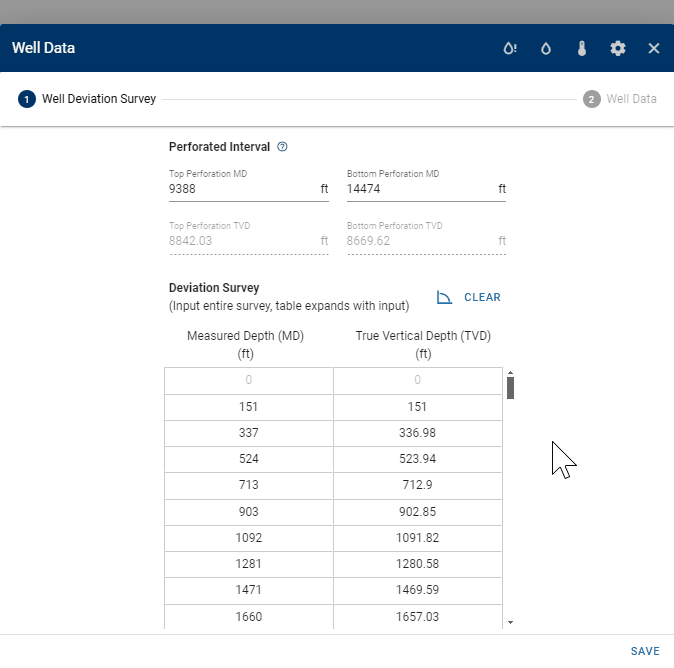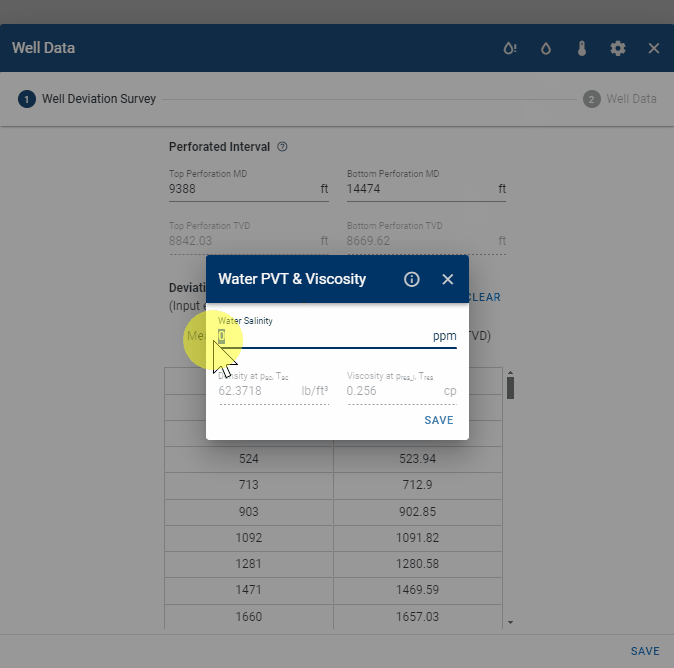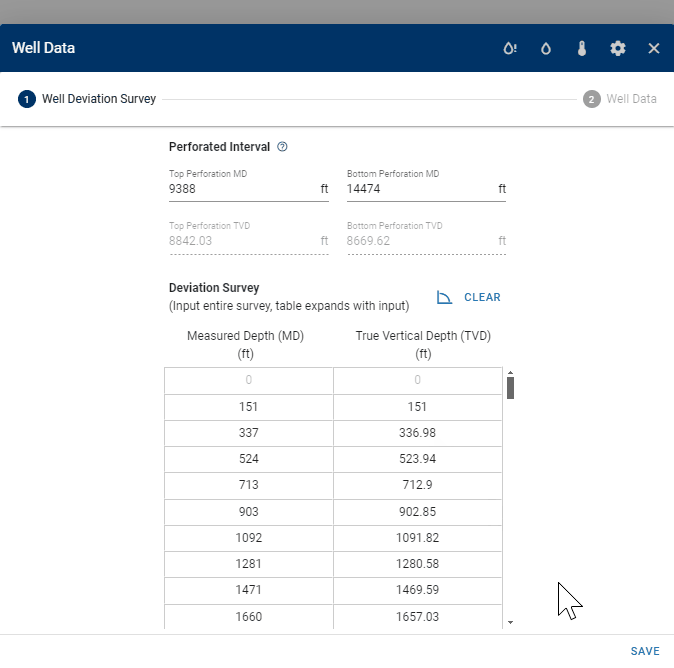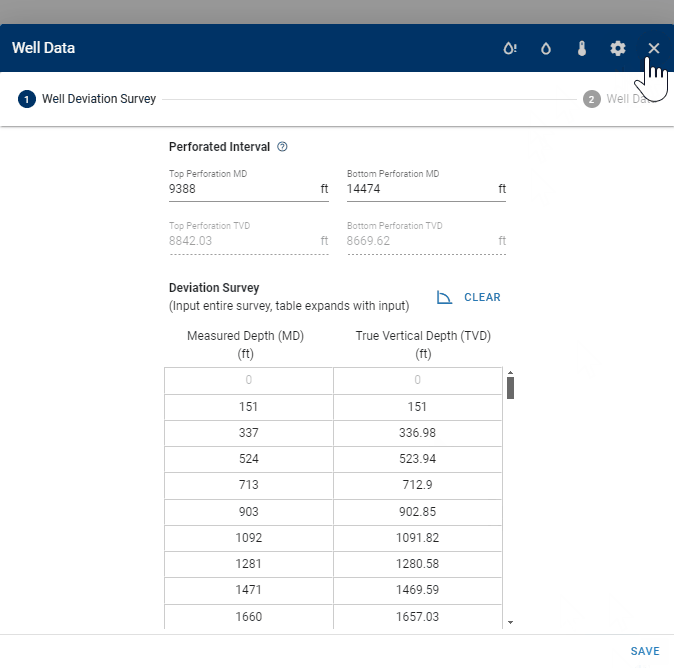
1.2 Well deviation survey

The well deviation survey describes the trajectory of the wellbore, and consists of a measured depth (MD) and calculated true vertical depth (TVD). The user can provide the full deviation survey of the well as the bhp module will sample the deviation survey backend to create the wellbore grid for BHP calculations. The perforated interval must be specified by providing the MD of the top- and bottom perforations. The top perforation is also the reference depth at which the BHP is calculated.

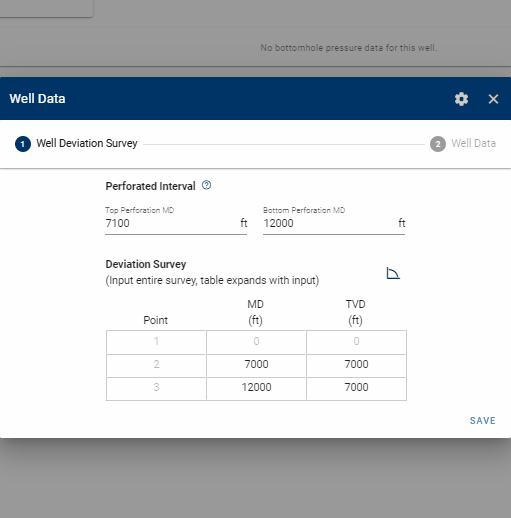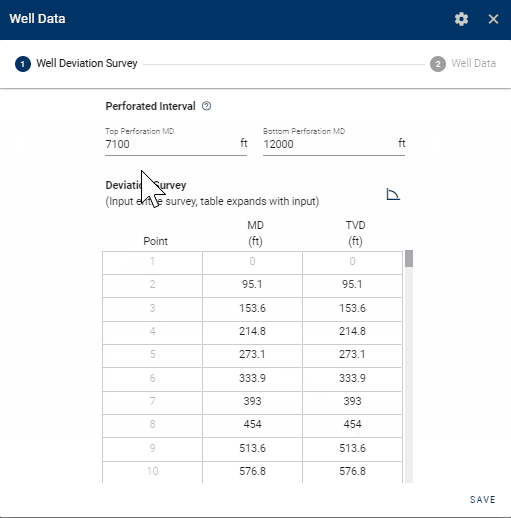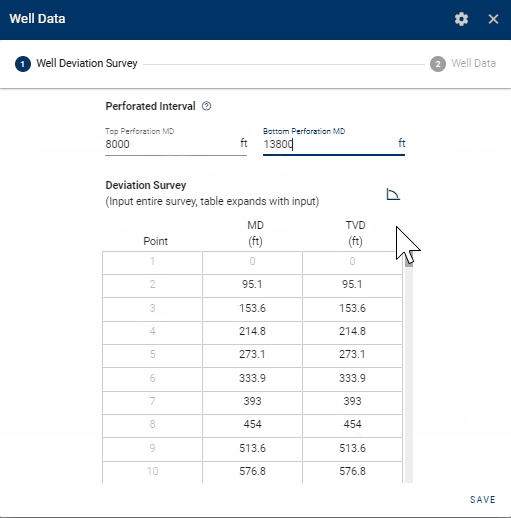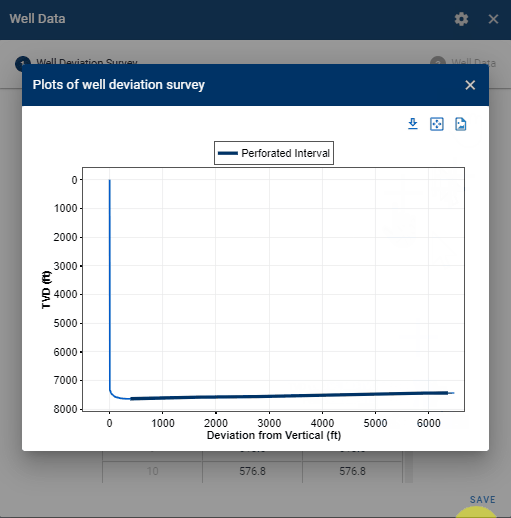
1.3 Well data

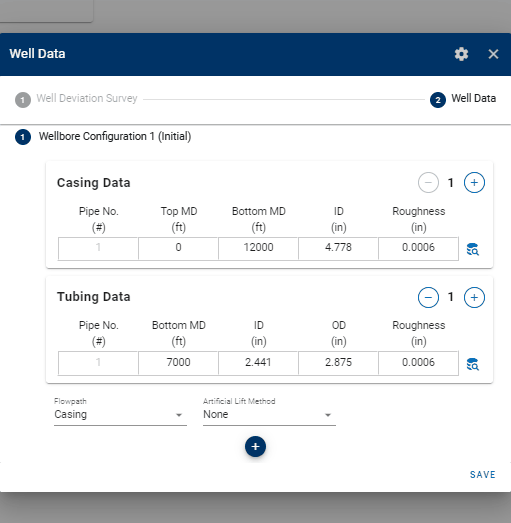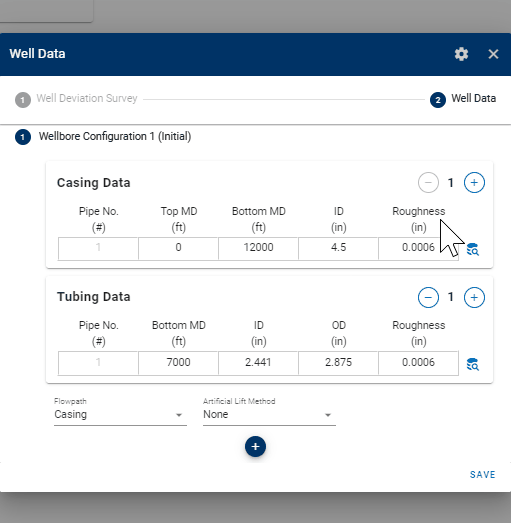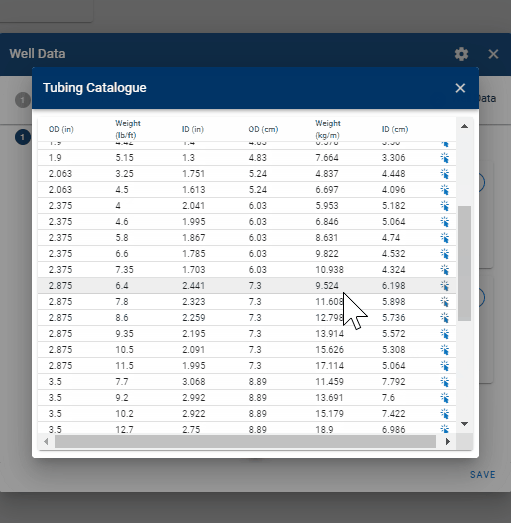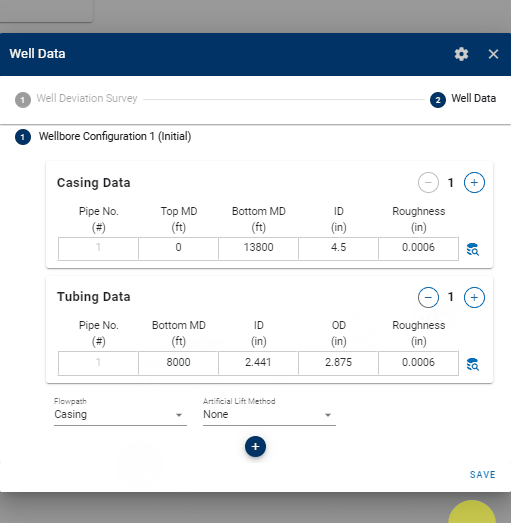
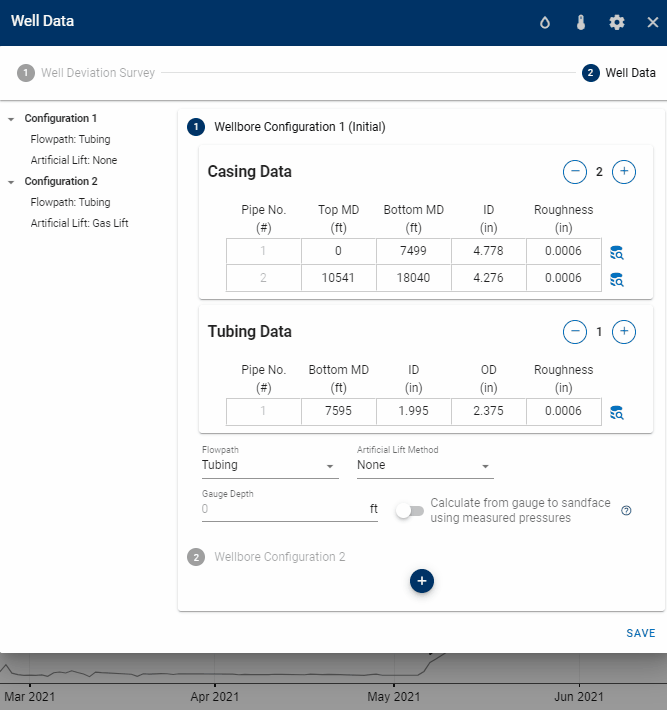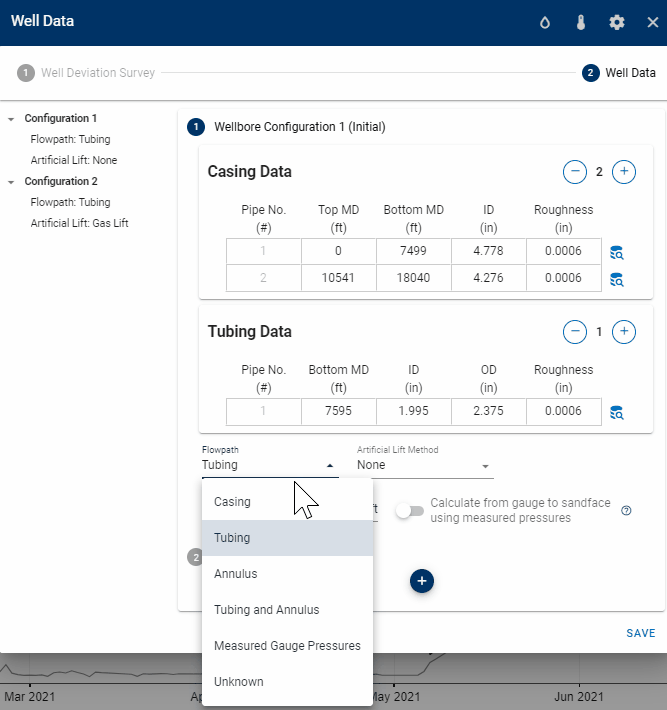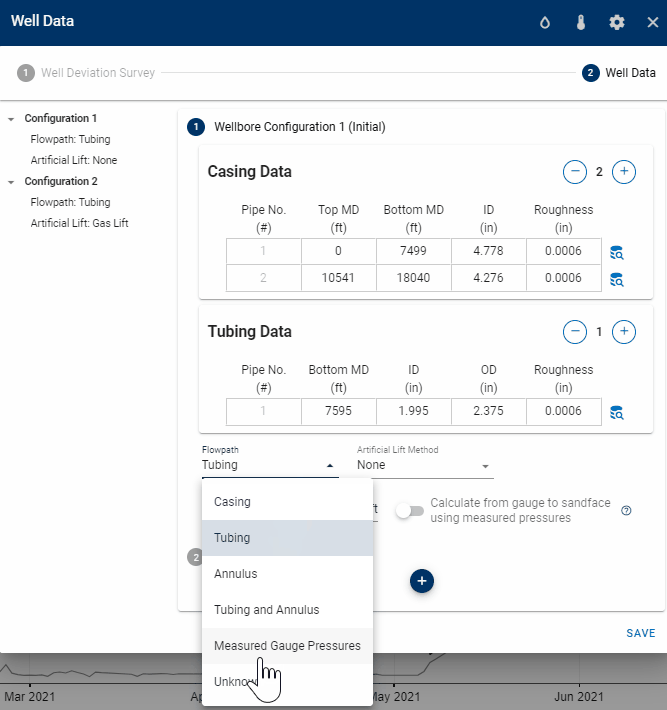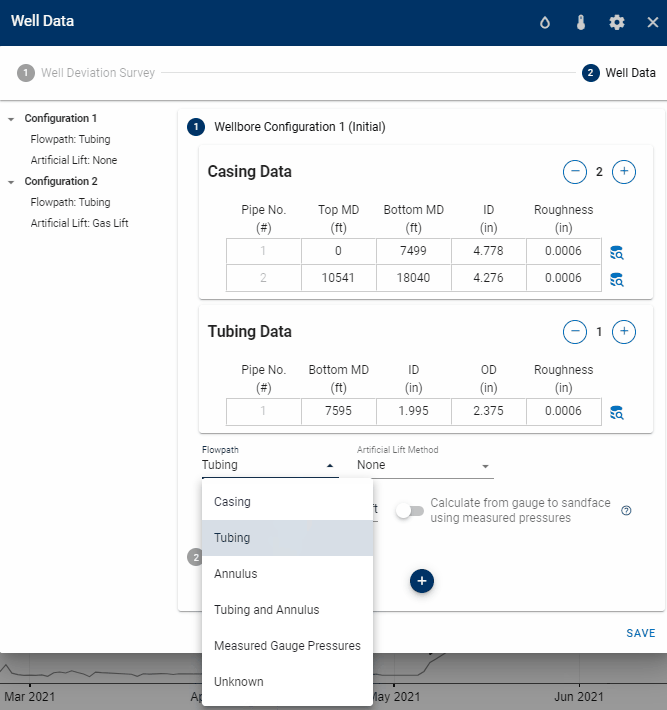
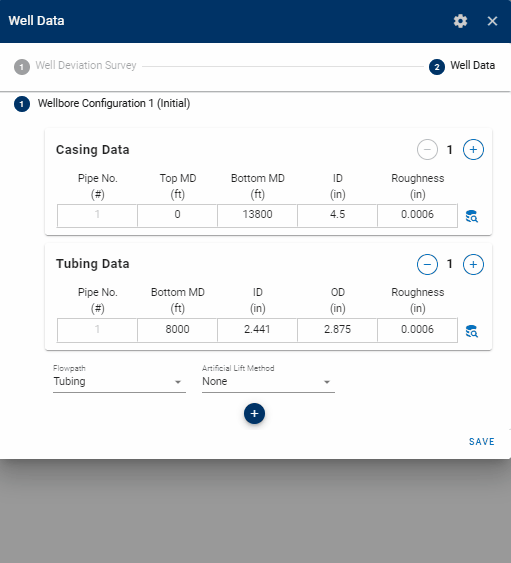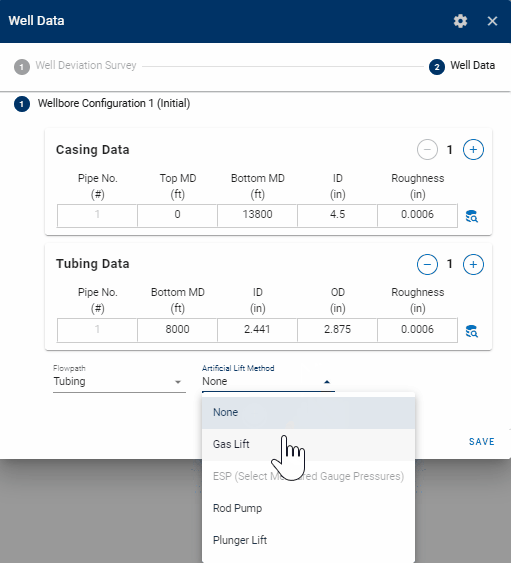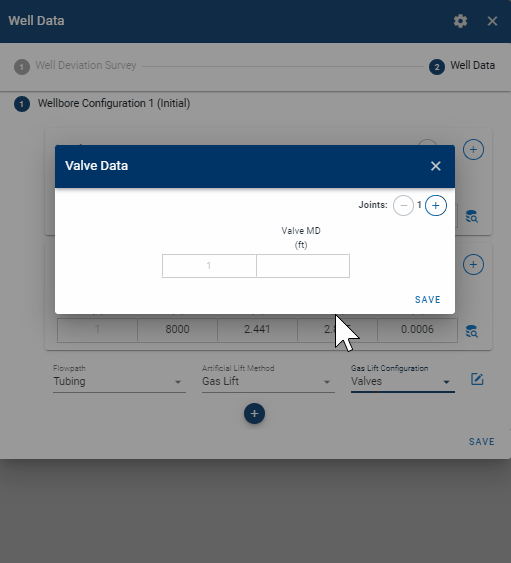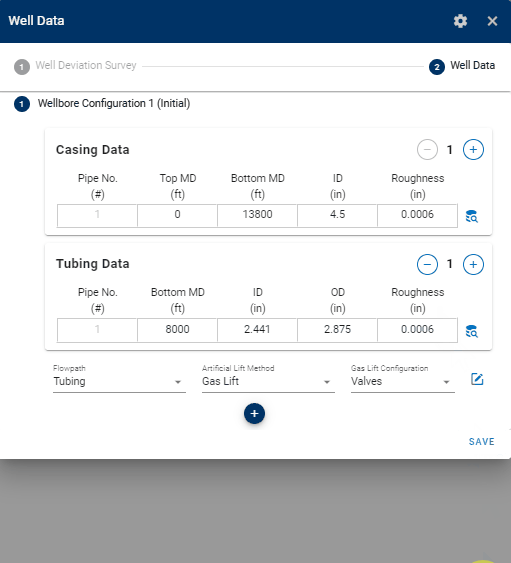
1.3.1 Casing- and Tubing Data

The well data consist of properties for the tubing- and casing string(s) relevant for pipe flow calculations, (i.e. the depths of the different pipes, their diameters, and roughnesses). Multiple tubing and casing strings can be specified, where an API tubing- and casing table is available to simplify the input of the pipe data.

1.3.2 Multiple Wellbore Configurations

Multiple completion data sets *wellbore configurations) can be specified, where a date must be set to tell the bhp module from which date in the production time series each completion is used.

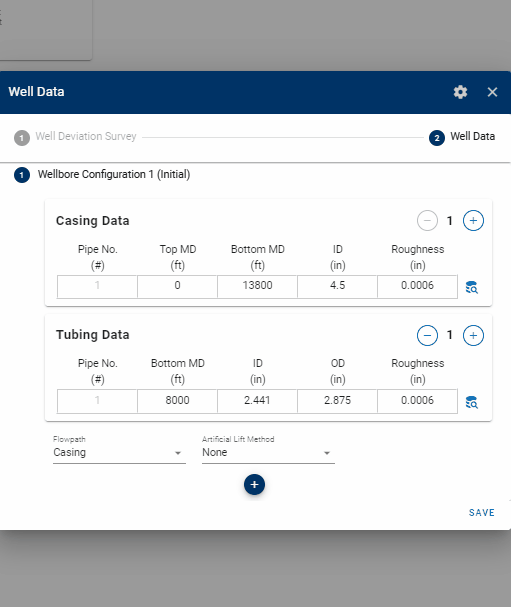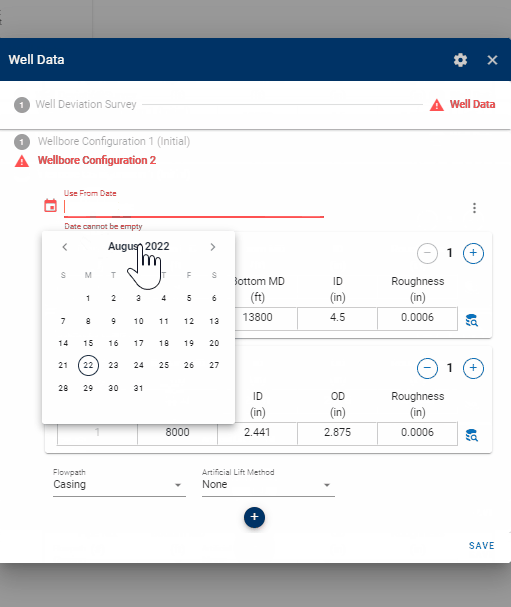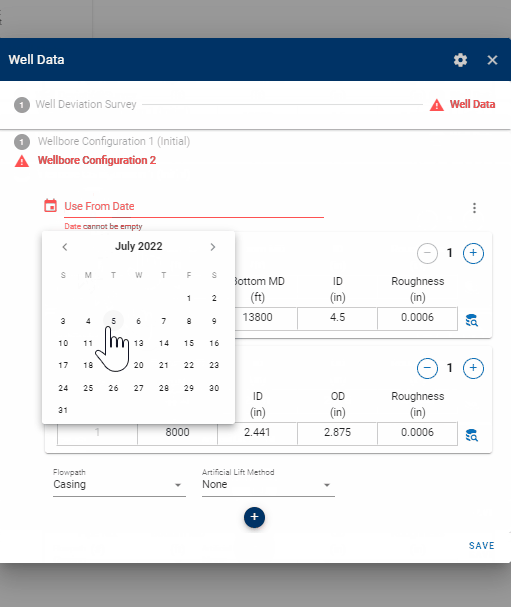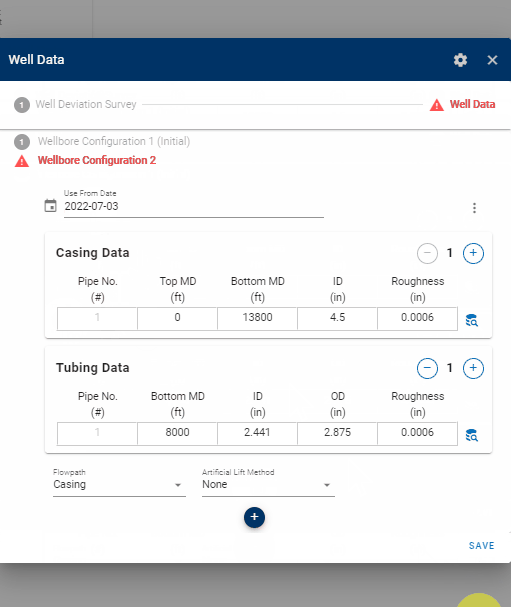
You can easily set the date for the new wellbore configuration graphically by clicking on the symbol adjacent to the date input field, as demonstrated in the .gif below. Then, simply align the vertical dashed line to the desired point in time when your new wellbore configuration should take effect.

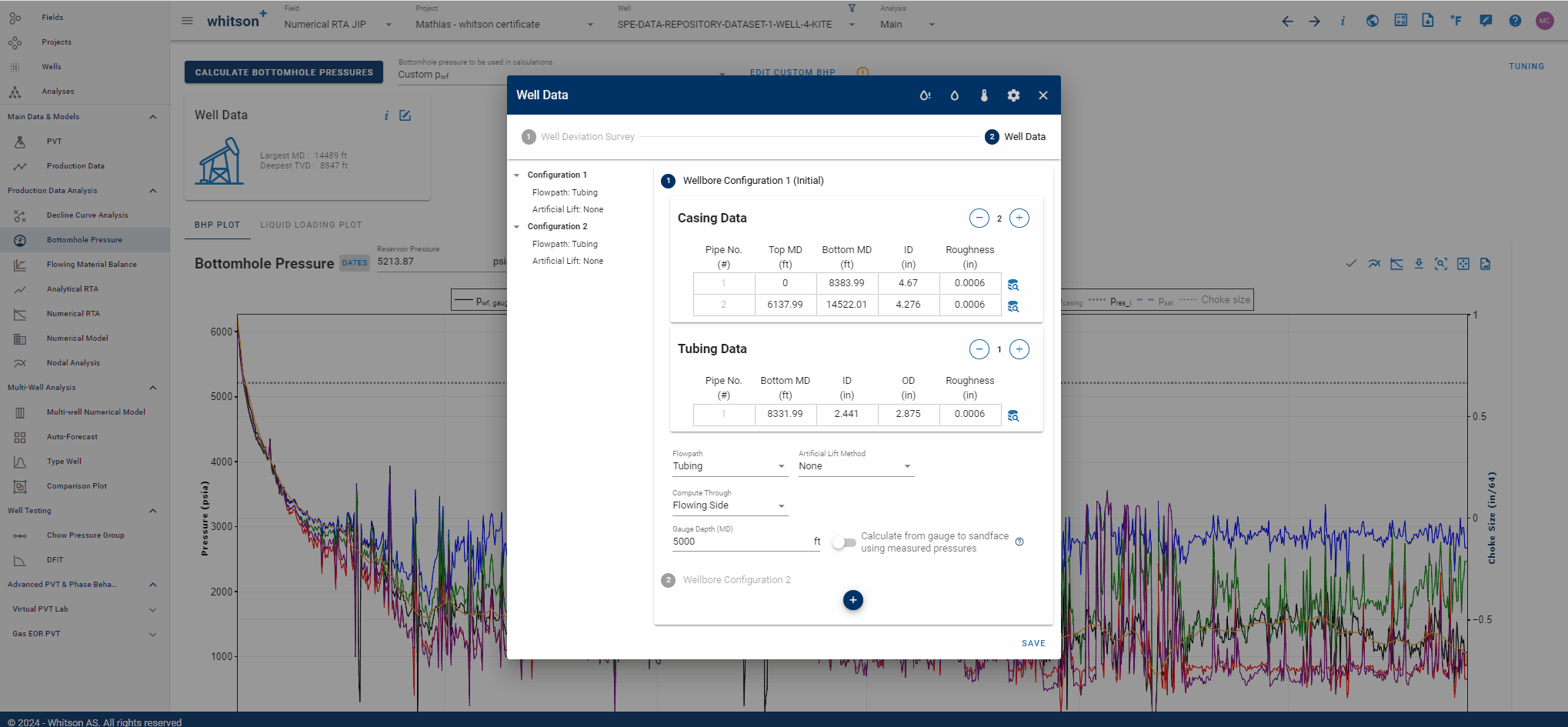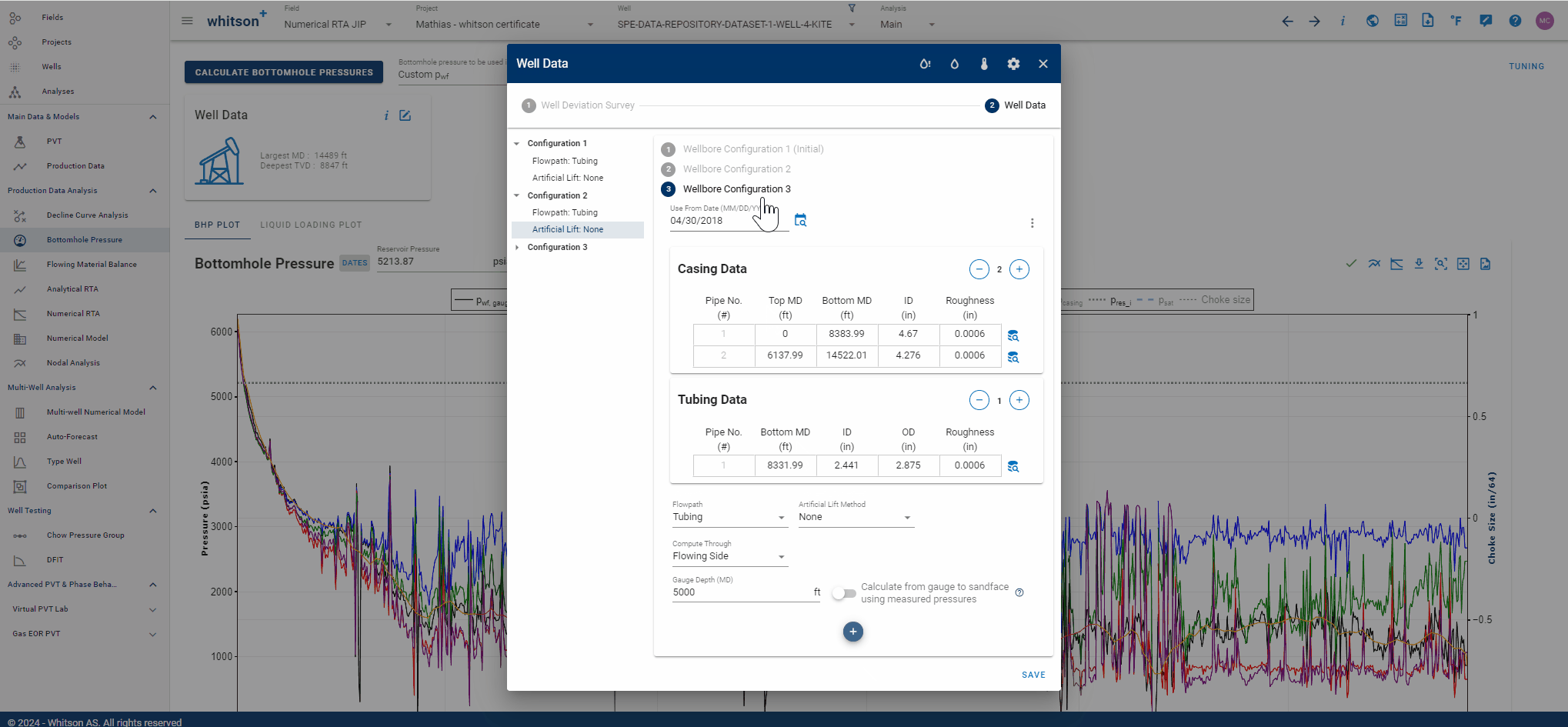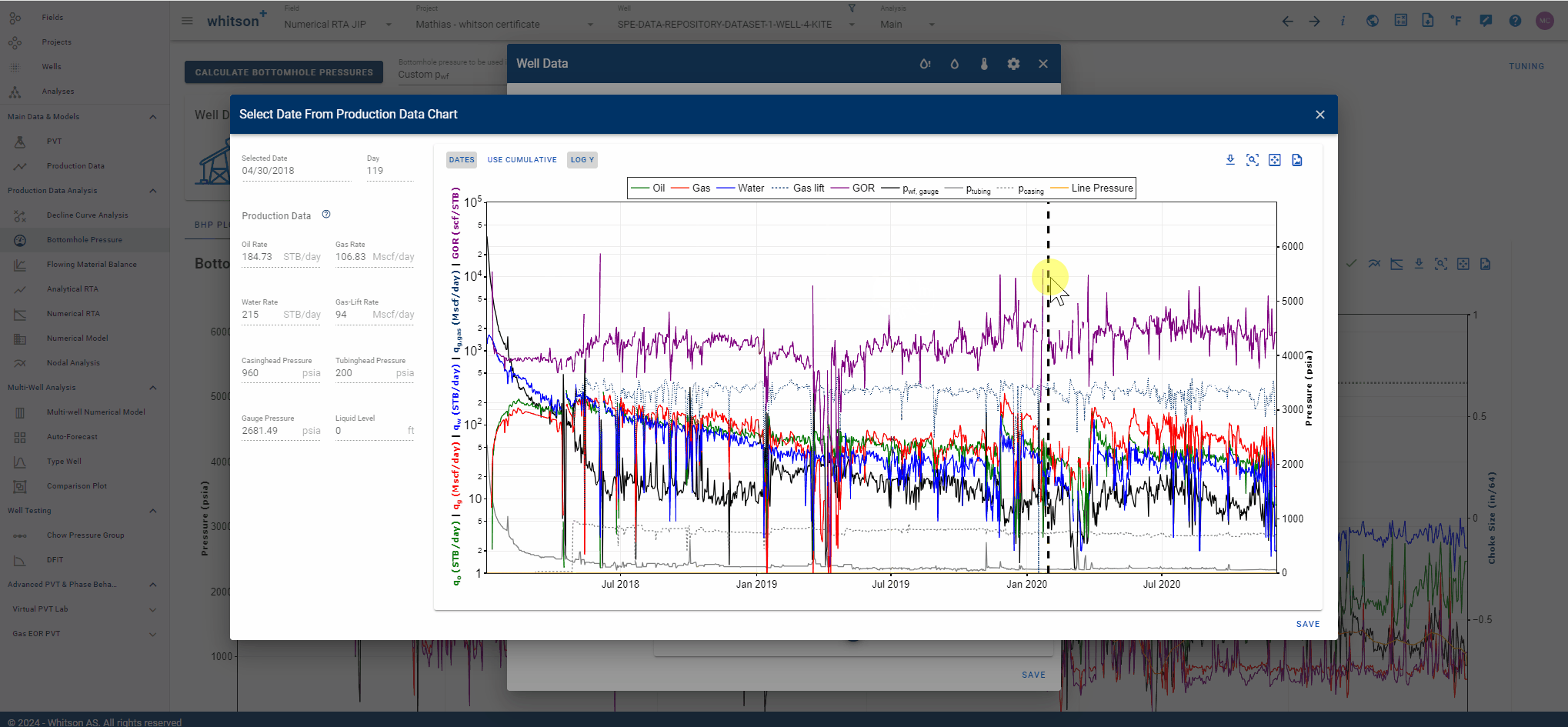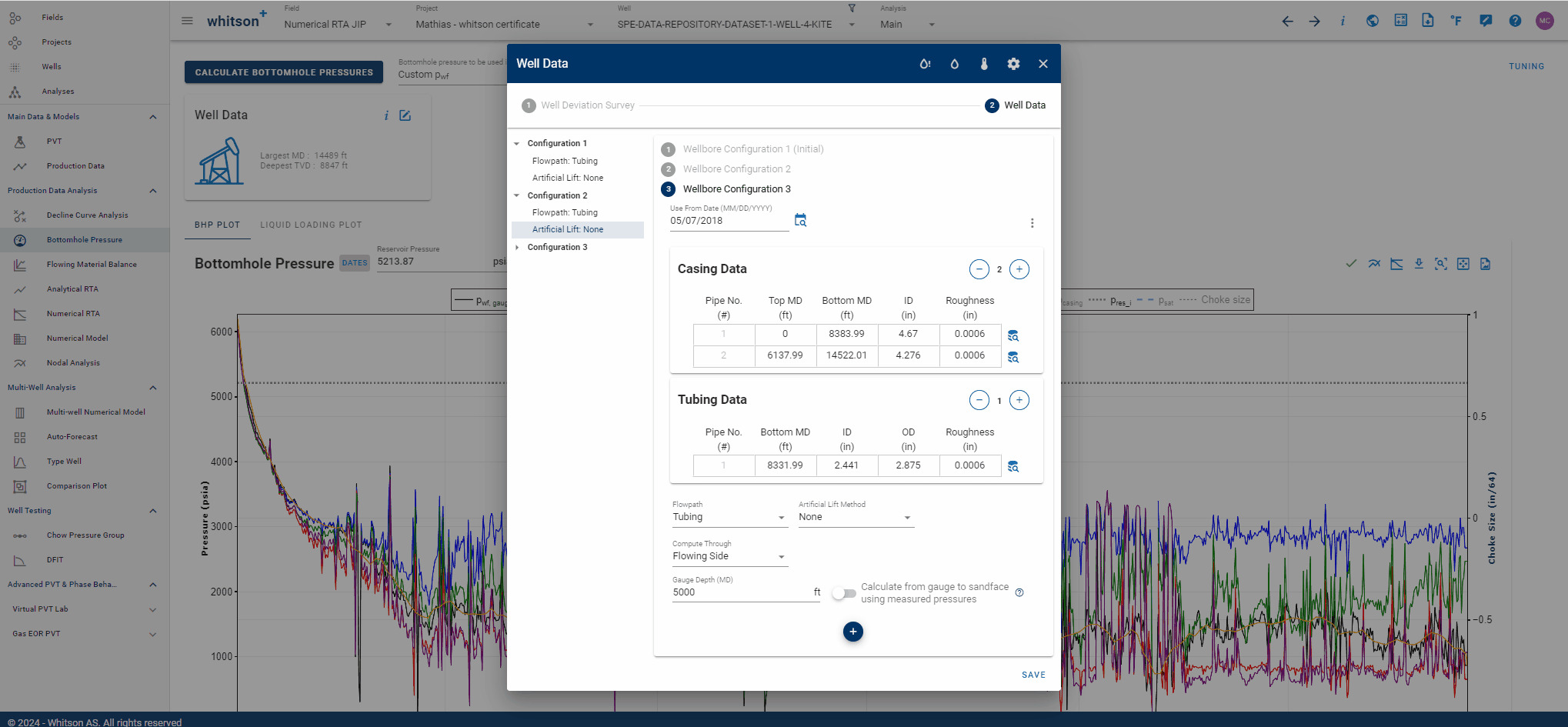
1.3.3 Flow Paths

The user must also specifiy the flow path of the wellstream for each wellbore configuration. The flow path can be:

• Tubing—Wellstream flows through a tubing string
• Casing—Wellstream flows through the production casing
• Annulus—Wellstream flows in the annulur space between the tubing and production casing
• Tubing & Annulus—Wellstream flows both through the tubing string and the annulur space between the tubing and production casing. See the section on dual conduit flow for further details.
• Measured BHP—If pressures from a downhole gauge have been provided under the Gauge Pressure column in production data, one can instruct the BHP model to echo the measured BHP (applies to wells for which an accurate estimate of the BHP is available, and where the user wants to include that pressure in the resulting BHP profile for completeness)
• Unknown—Automatic selection of flow path depending on the casinghead pressure, tubinghead pressure, and associated well configuration. The following table summarizes the logic applied for the unknown flow path.

Condition	Selected Flow Path
\(p_{casing}\) \(>\) \(p_{tubing}\) and Tubing is Installed	Tubing
\(p_{casing}\) \(\leq\) \(p_{tubing}\) and Tubing is Installed	Annulus
Tubing is not Installed	Casing

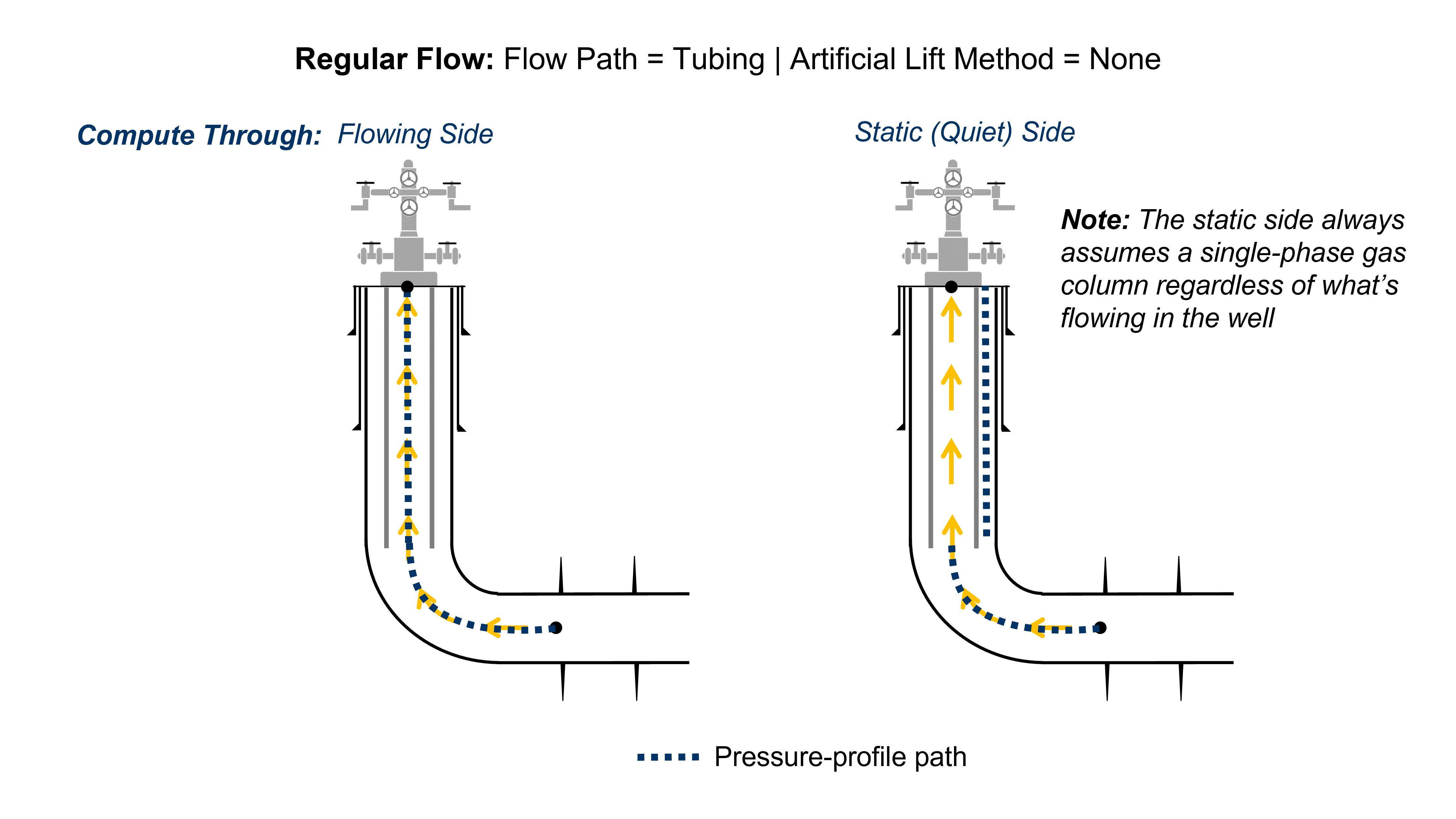
1.3.4 Static (Quiet) Side

The user may select which side of the tubing the bottomhole-pressure calculation should follow. Using the static (quiet) side of the tubing assumes that there is a single-phase gas column with communication to the flowing side at the EOT (i.e., no isolating packer).

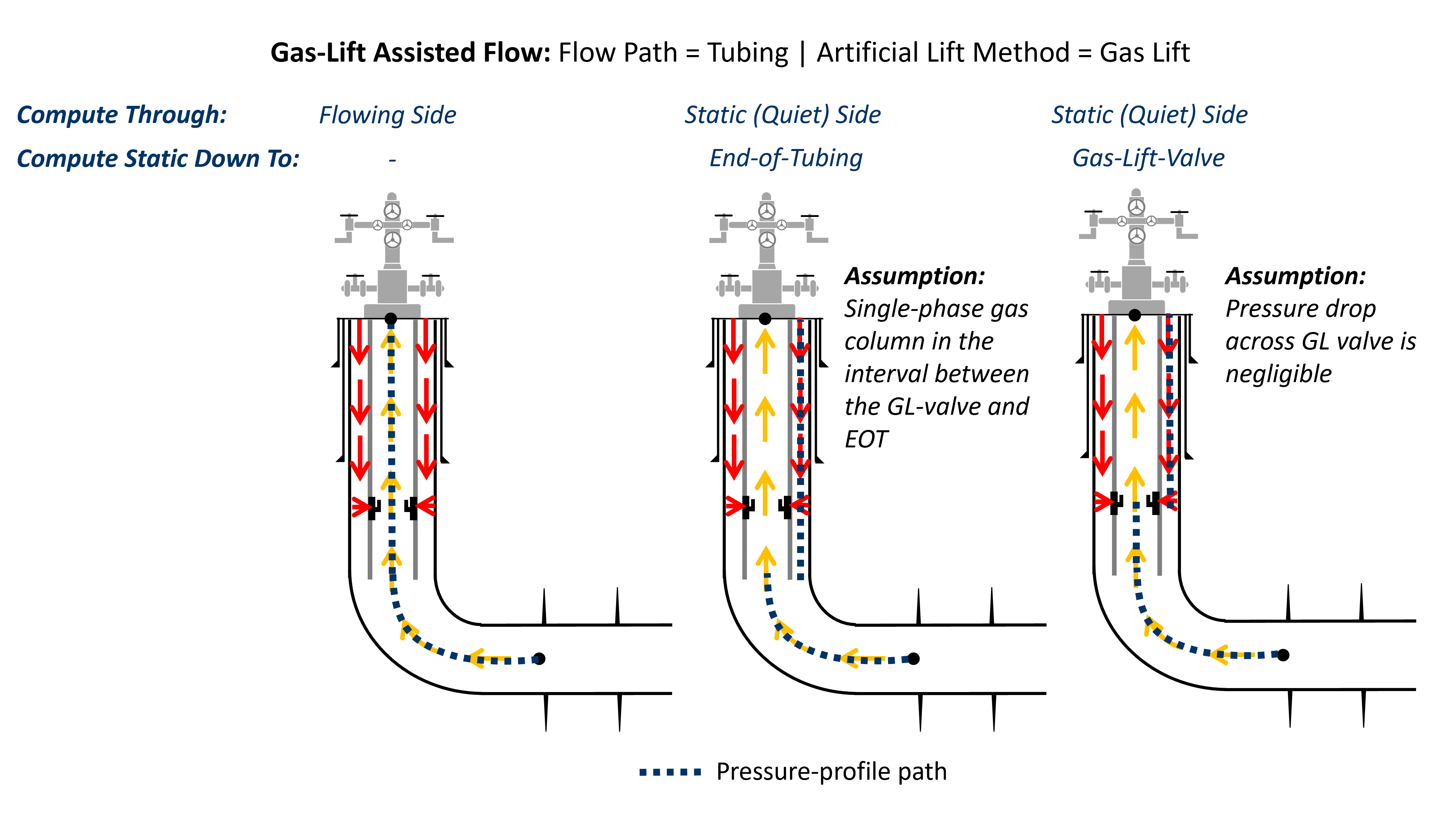
The static-side calculation is well suited for gas-lift assisted wells where it is certain that the static side is filled with gas at least down to the gas-lift valve. The figures below explain how the static-side calculation works for a naturally flowing well, and a gas-lift assisted well. The flow path in this case is set to "tubing", but the static-side calculation also works when the flow path is set to "annulus", with everything being reversed compared to the figures below.

For gas-lift assisted wells where the gas-lift configuration is set to "valves" or "automatic", it is also possible to select whether to do the static-side calculation down to the gas-lift valve or to the end of the tubing.

1.3.5 Convert from Gauge Pressure to Sandface

If the user has entered pressures for one or several rows in the Gauge Pressure column in production data, one can convert from this pressure and down to sandface. To do this, toggle on "Calculate from gauge to sandface using measured pressures".

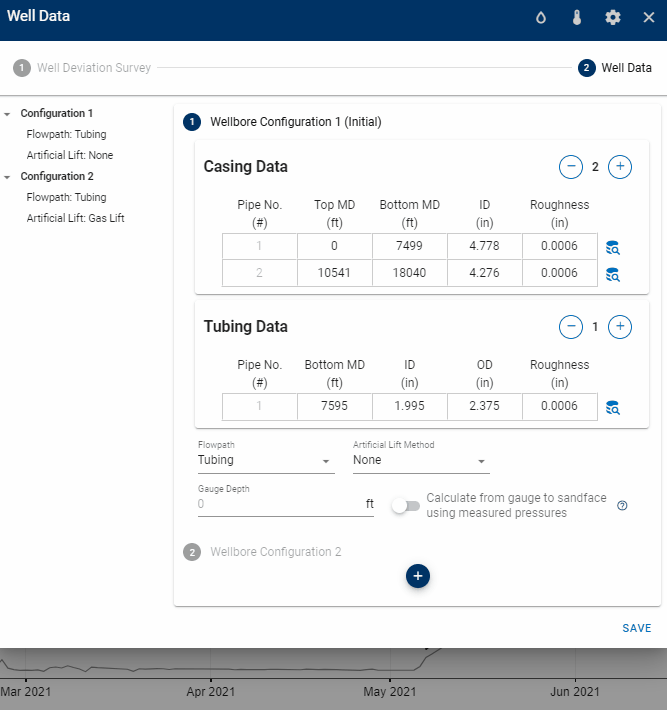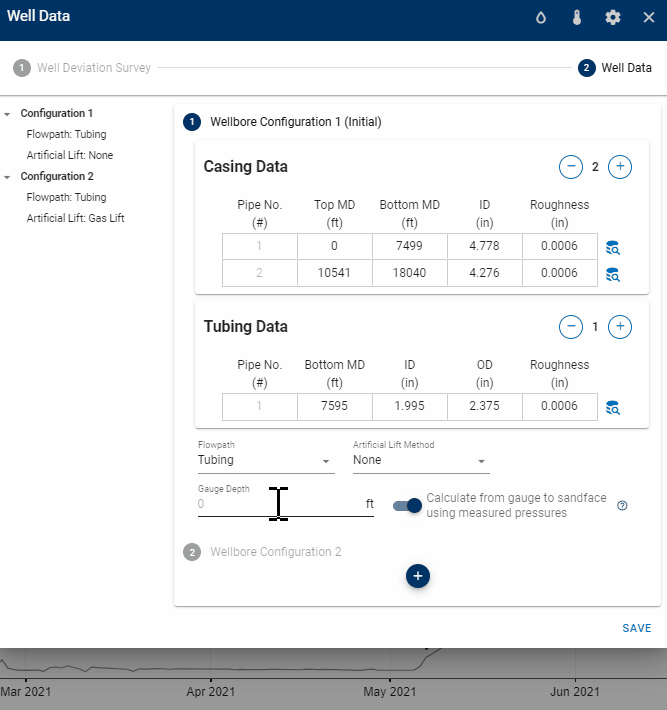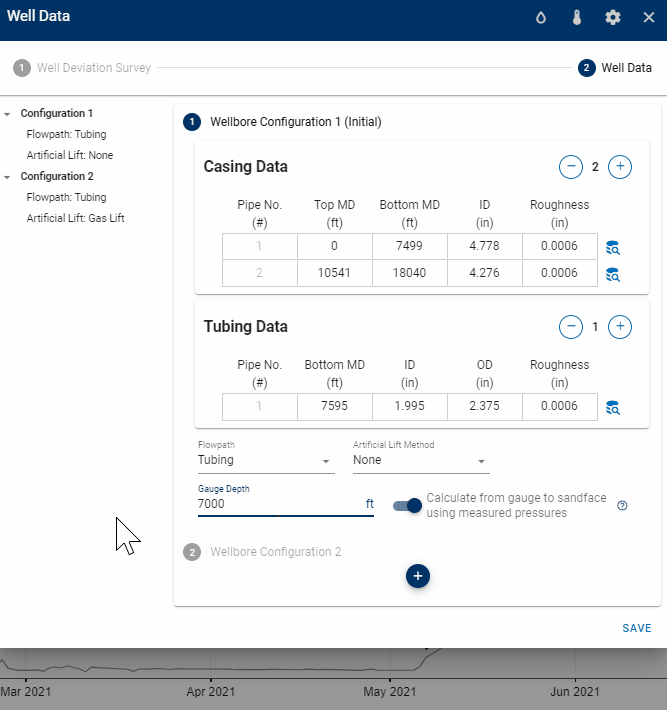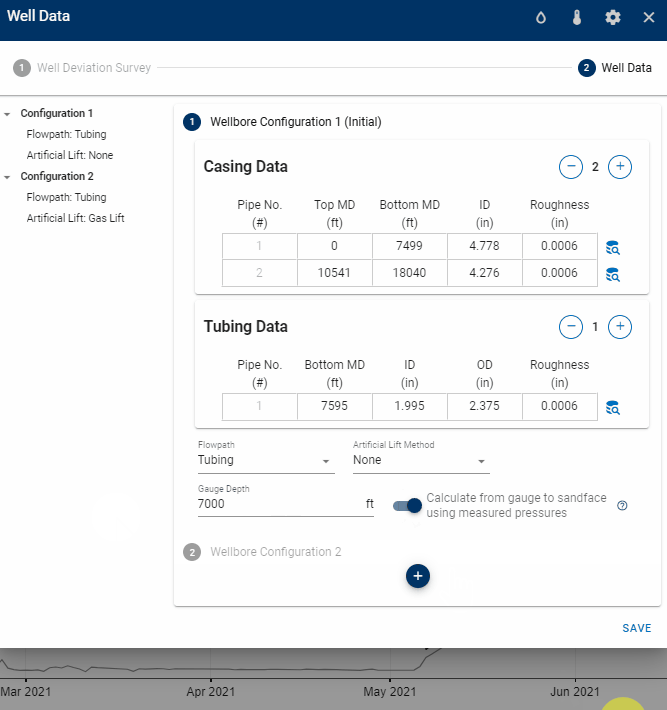
When the "Calculate from gauge to sandface using measured pressures" switch is activated, the behavior of the software is going to be dependent on whether a gauge depth is provided or not.

1. If a gauge depth is provided, the software will correct the gauge pressure from that gauge depth to top perforation depth.

2. If a gauge depth is not provided, the software will continue calculating the BHPs as if the switch was not activated.

So basically, for the activation of the switch to be useful for your purposes, ensure that you have provided the gauge depth within the corresponding wellbore configuration.

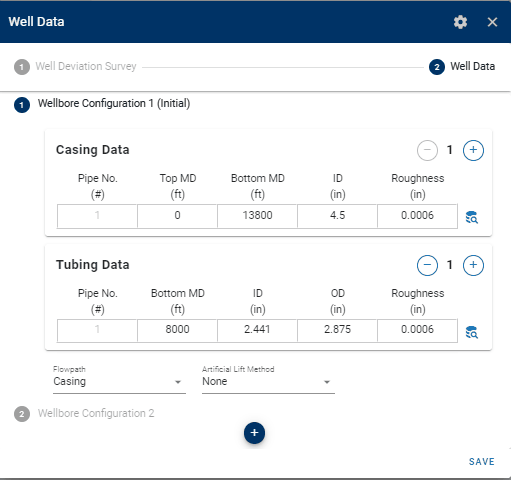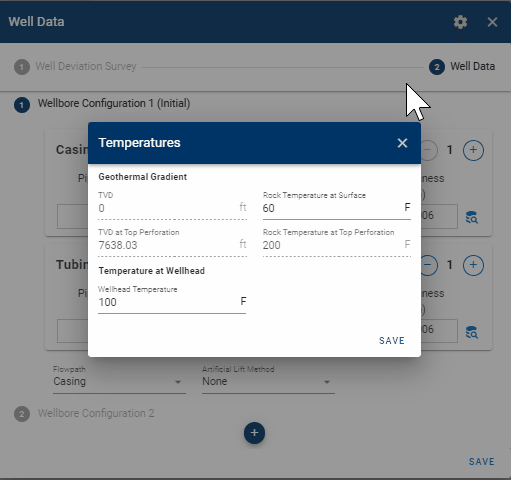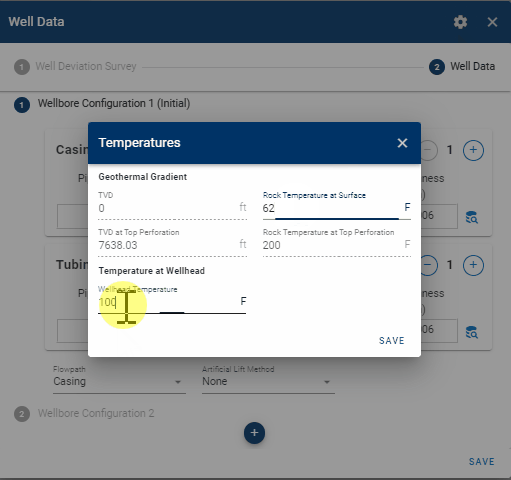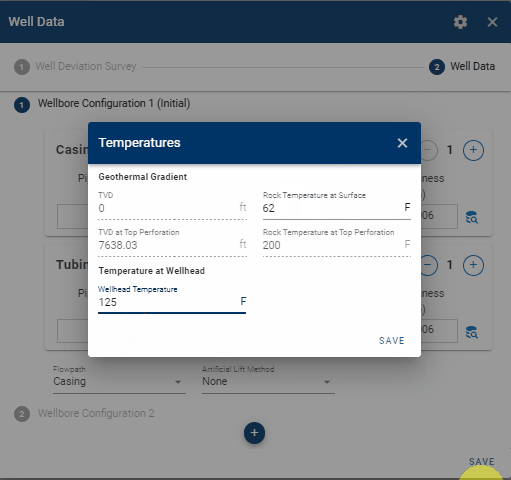
1.4 Temperature Data

The temperature data require two inputs, the rock temperature at the surface (to create the linear temperature profile in the rock), and the average wellhead temperature for the production time series.

1.5 Water properties

Water data requires only water salinity as input. Water density and viscosity are calculated automatically.

1.6 Artificial-Lift Data

The BHP can be calculated while the well is on gas-lift, rod pump or plunger lift.

Gas lift is active for a given day if the active wellbore configuration for that day has gas lift as the artificial lift method, and \(q_{g,gas lift}\) in the production data is greater than zero.

Rod pump is active for a given day if the active wellbore configuration for that day has rod pump as the artificial lift method, and the "Liquid Level" in the production data is greater than zero.

Plunger lift is active for a given day if the active wellbore configuration for that day has plunger lift as the artificial lift method, and the "Liquid Level" in the production data is greater than zero.

ESP (Electric Submersible Pump) can only be activated if downhole pressures are measured at the inlet of the ESP with a pressure gauge. If this option is selected, the user can provide the depth of the pressure gauge, and correct the pressures from measurement point down to sandface.

2. Output

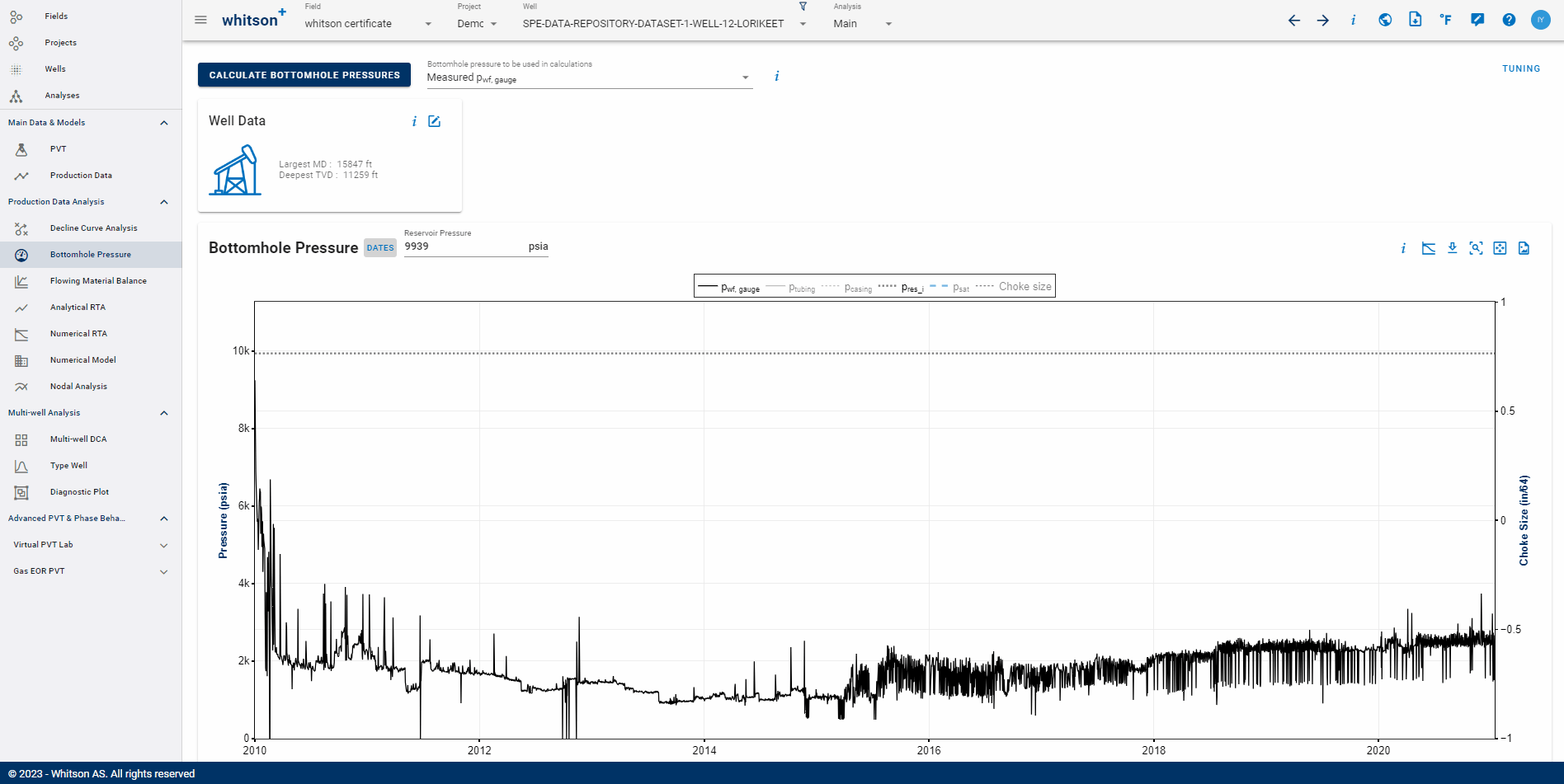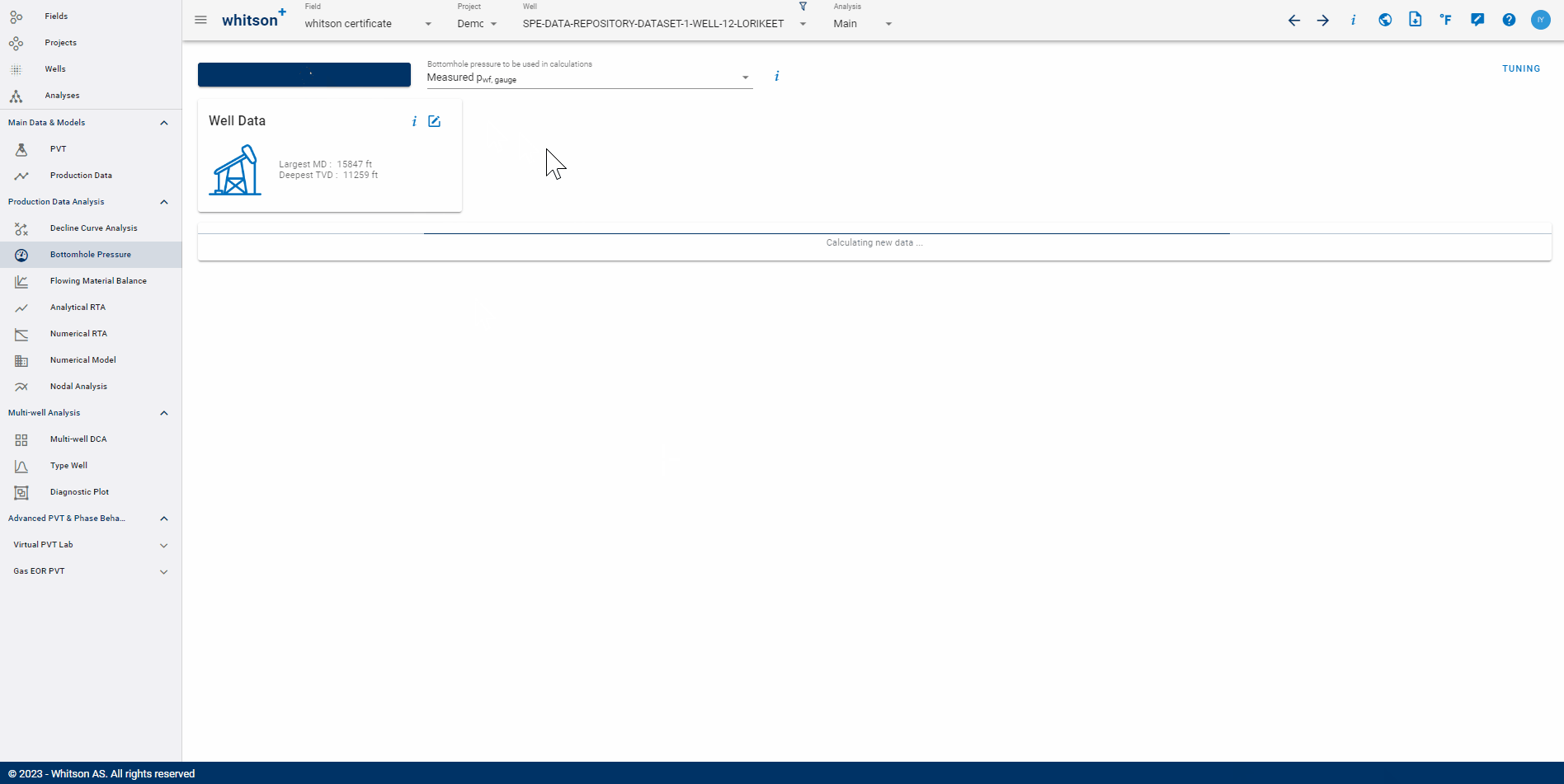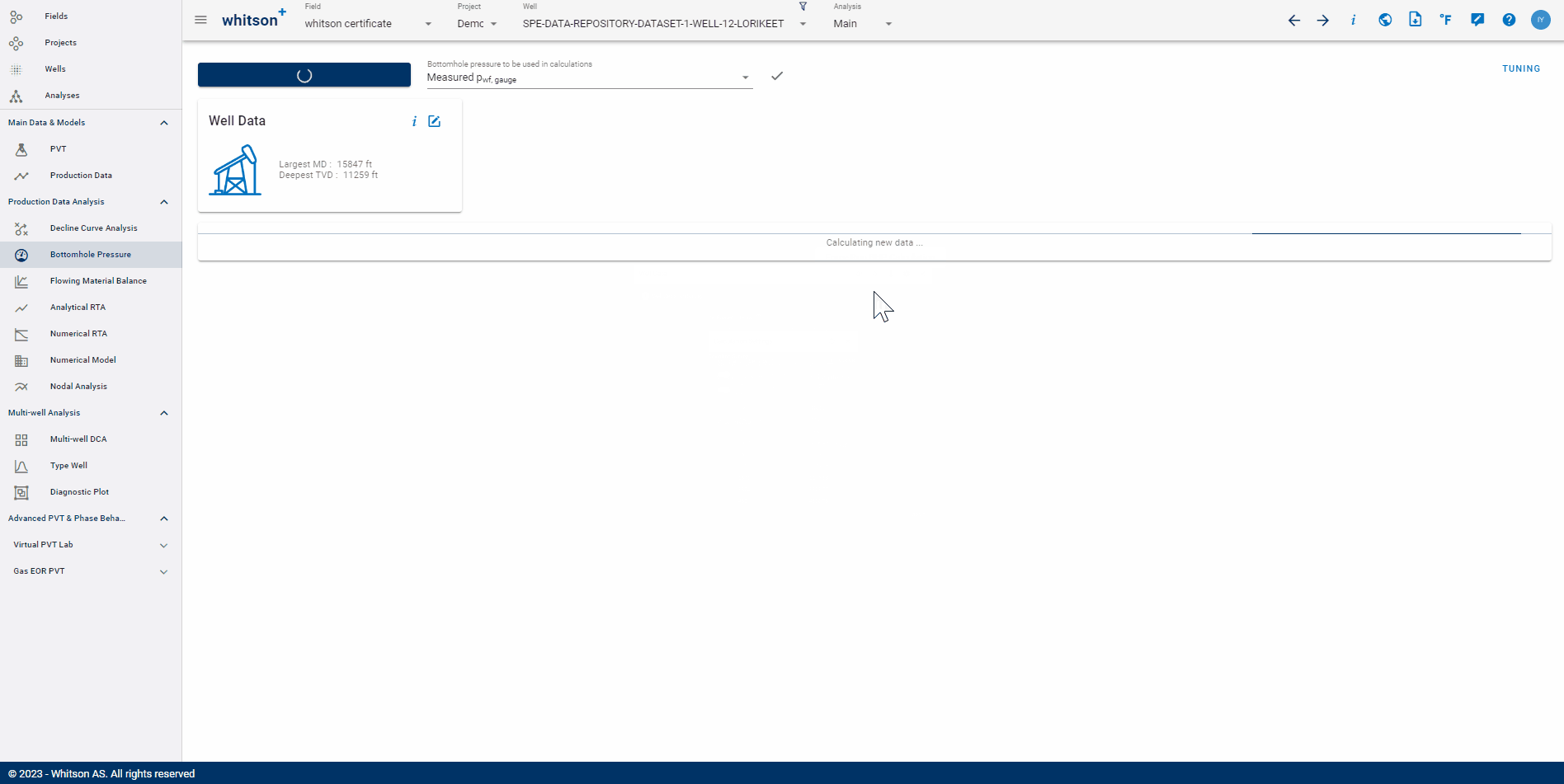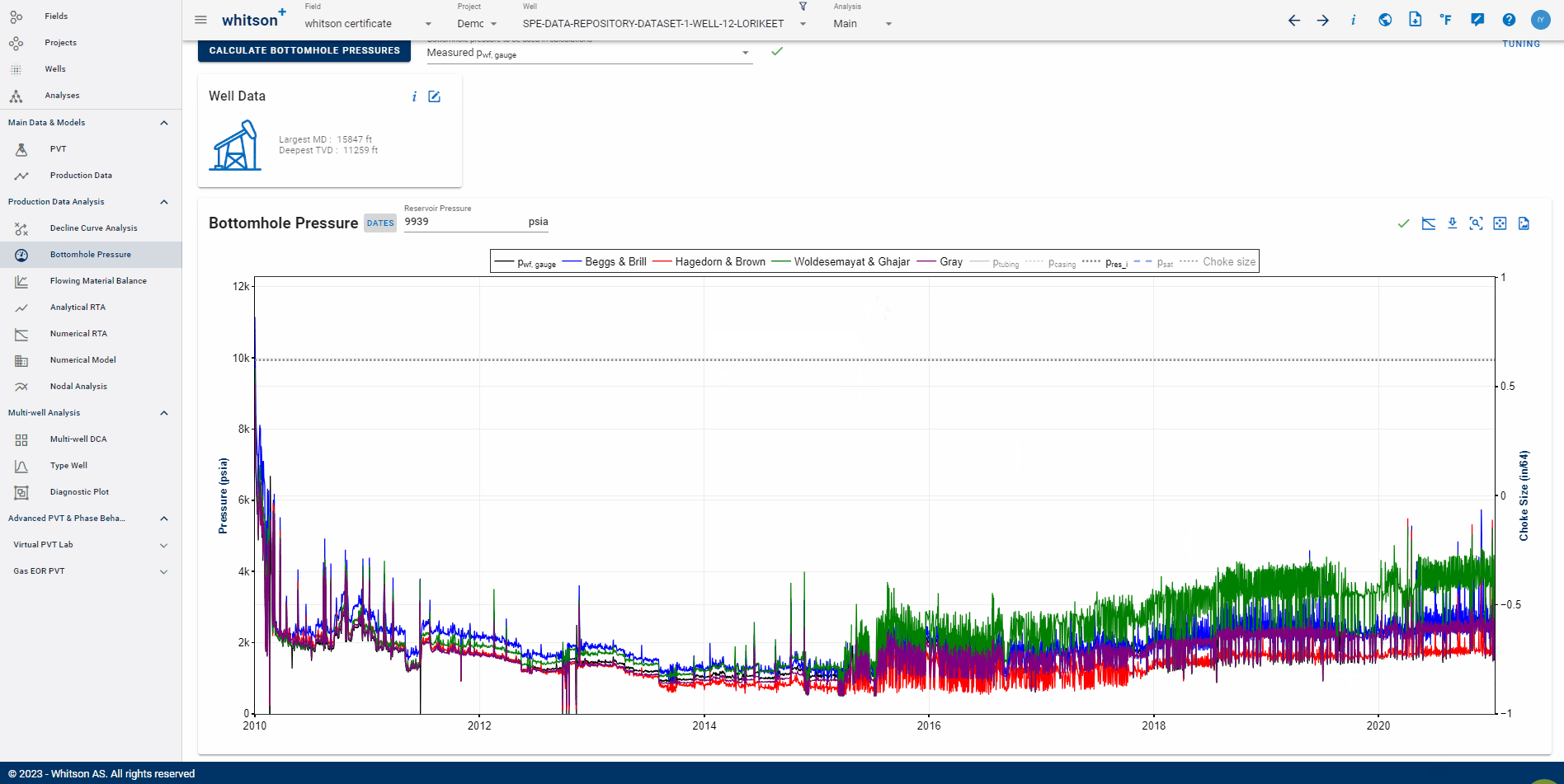
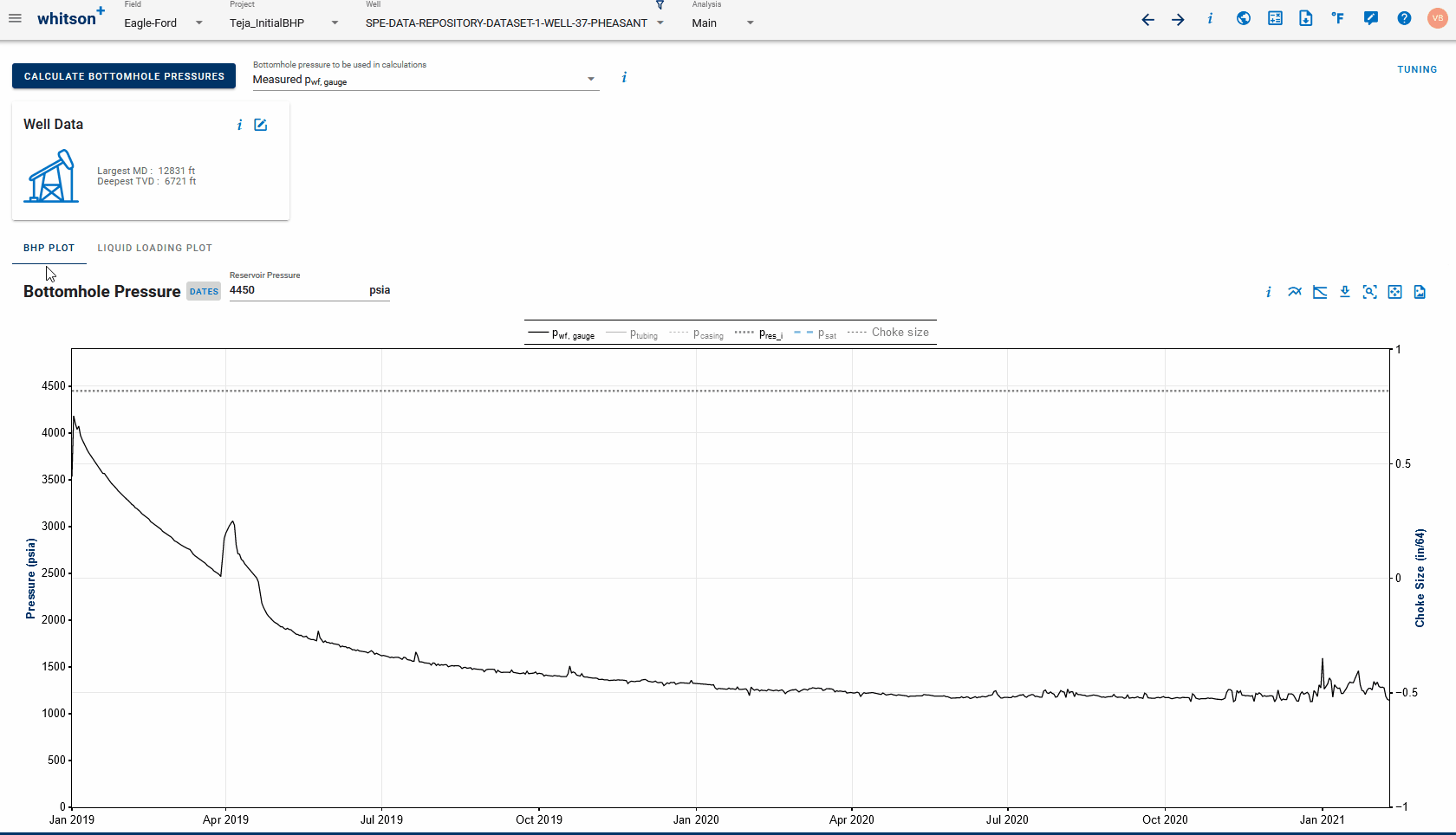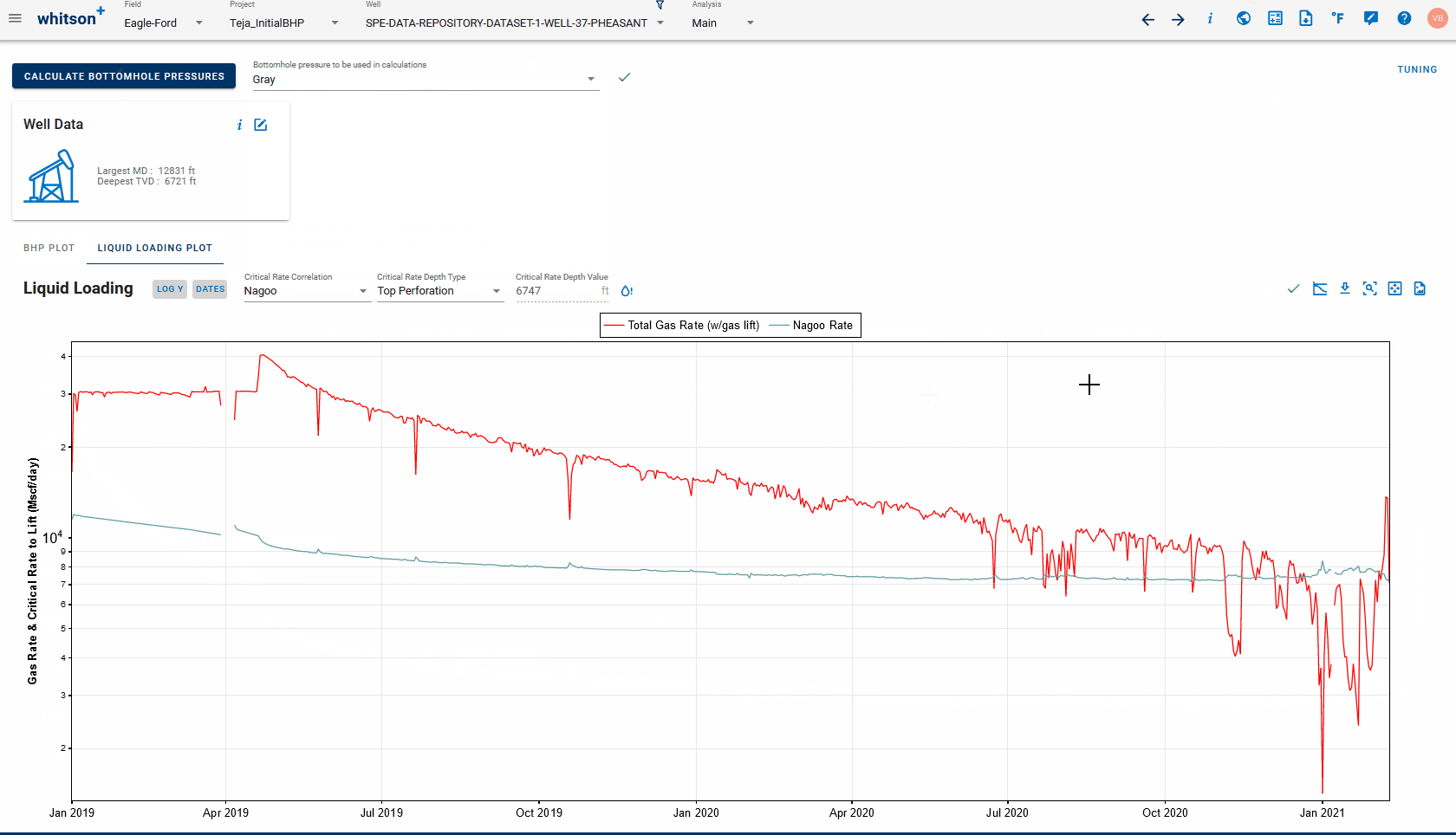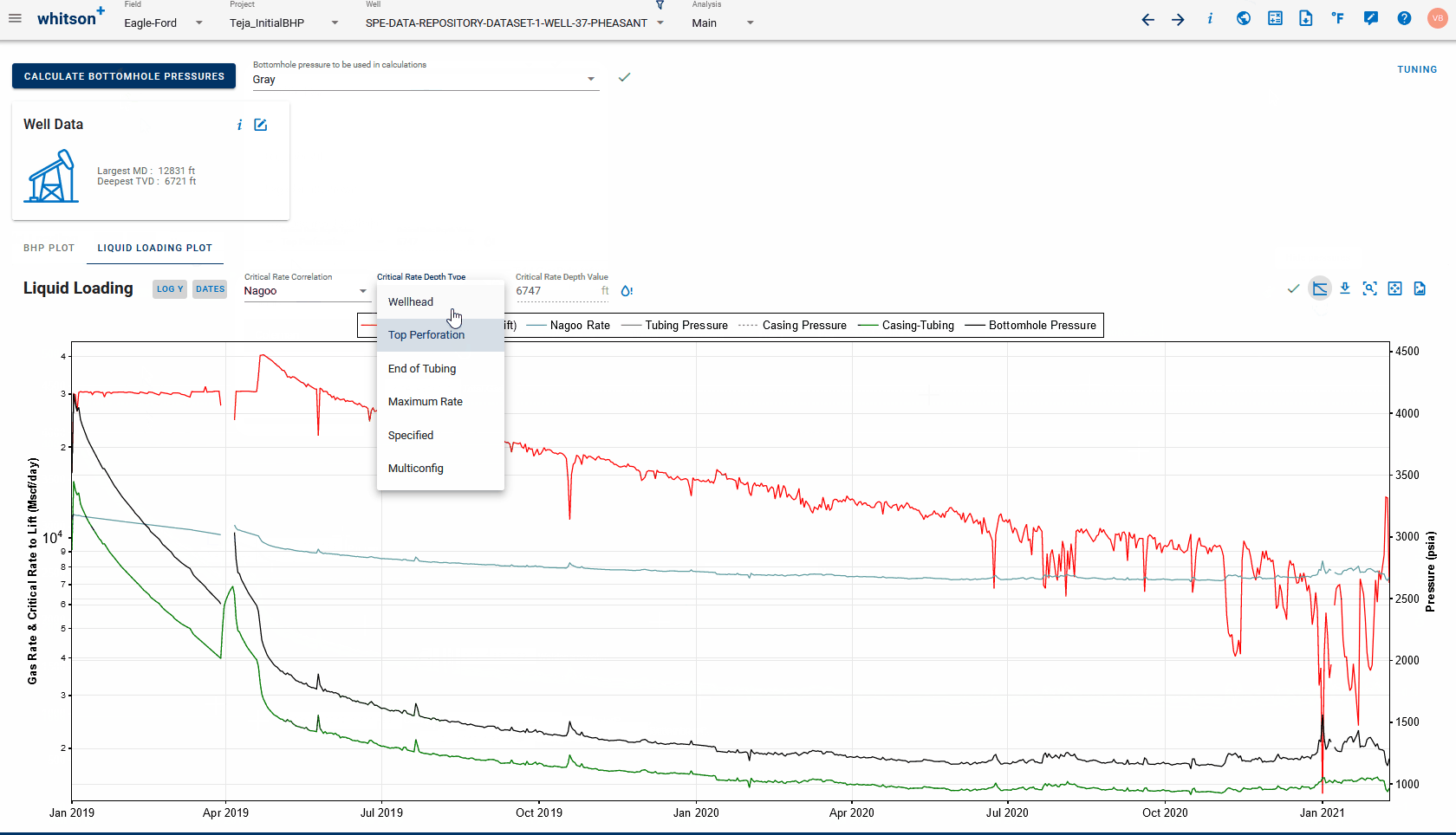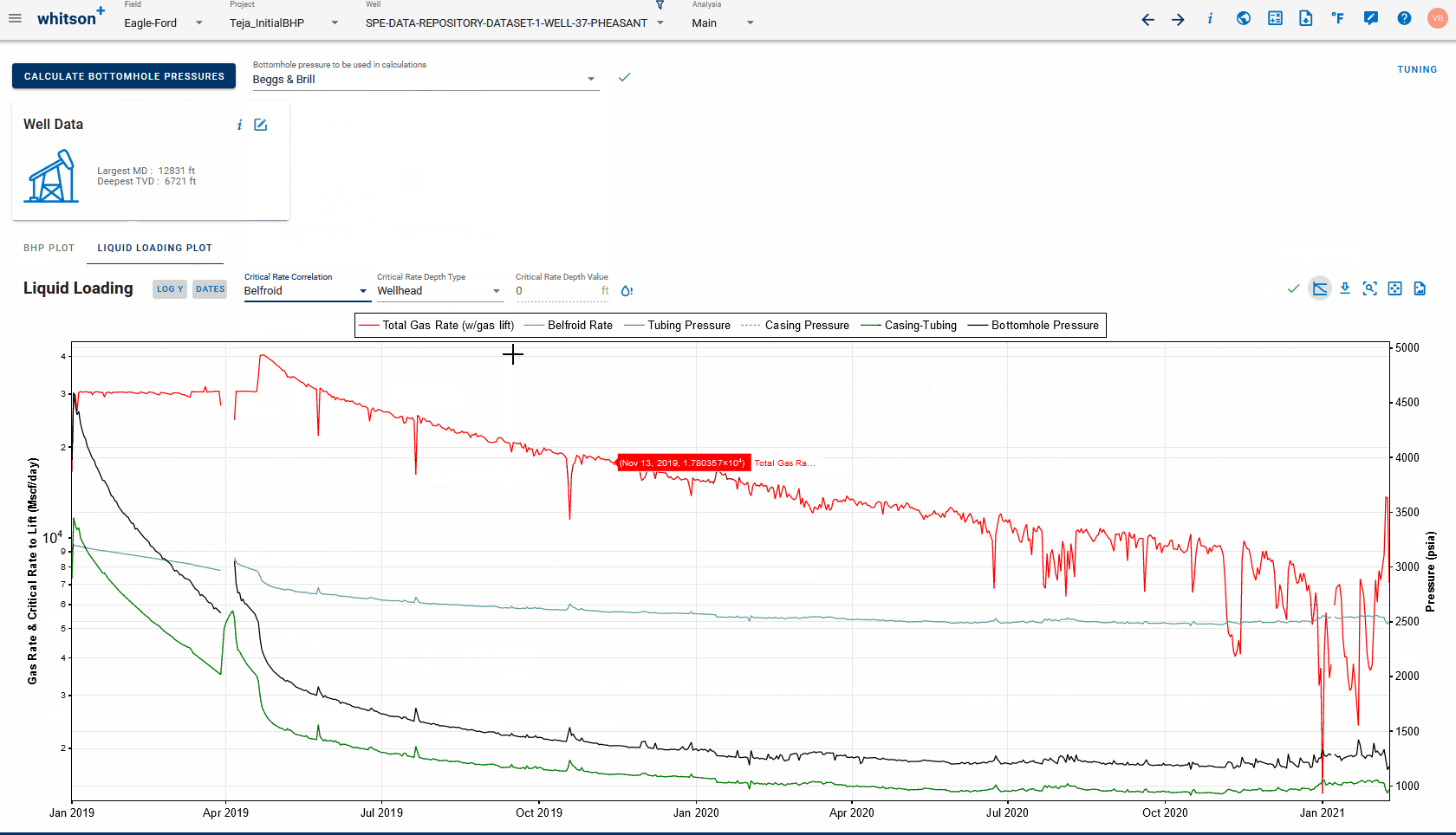
2.1 Output Curves

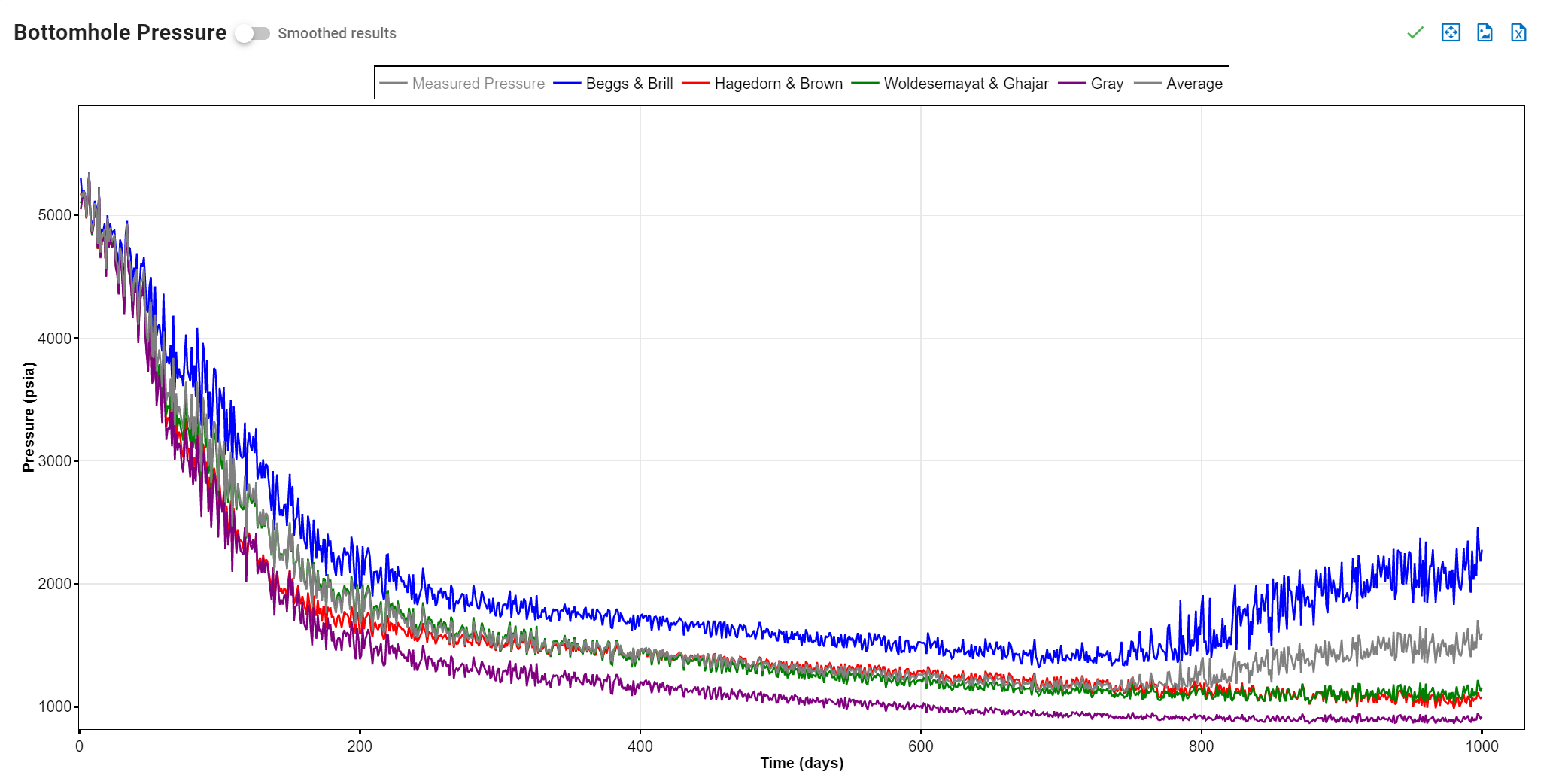
The output data for the BHP module is the calculated bottomhole pressure, at the top perforation depth, for every entry in the production time series. The user can choose whether to use the noicy data resulting from noicy production data, or to apply a smoothening of the data. Furthermore, the user can select which BHP data set to use in other features of whitson+ that rely on bottomhole pressures. This ensures consistency in all calculations across the platform.

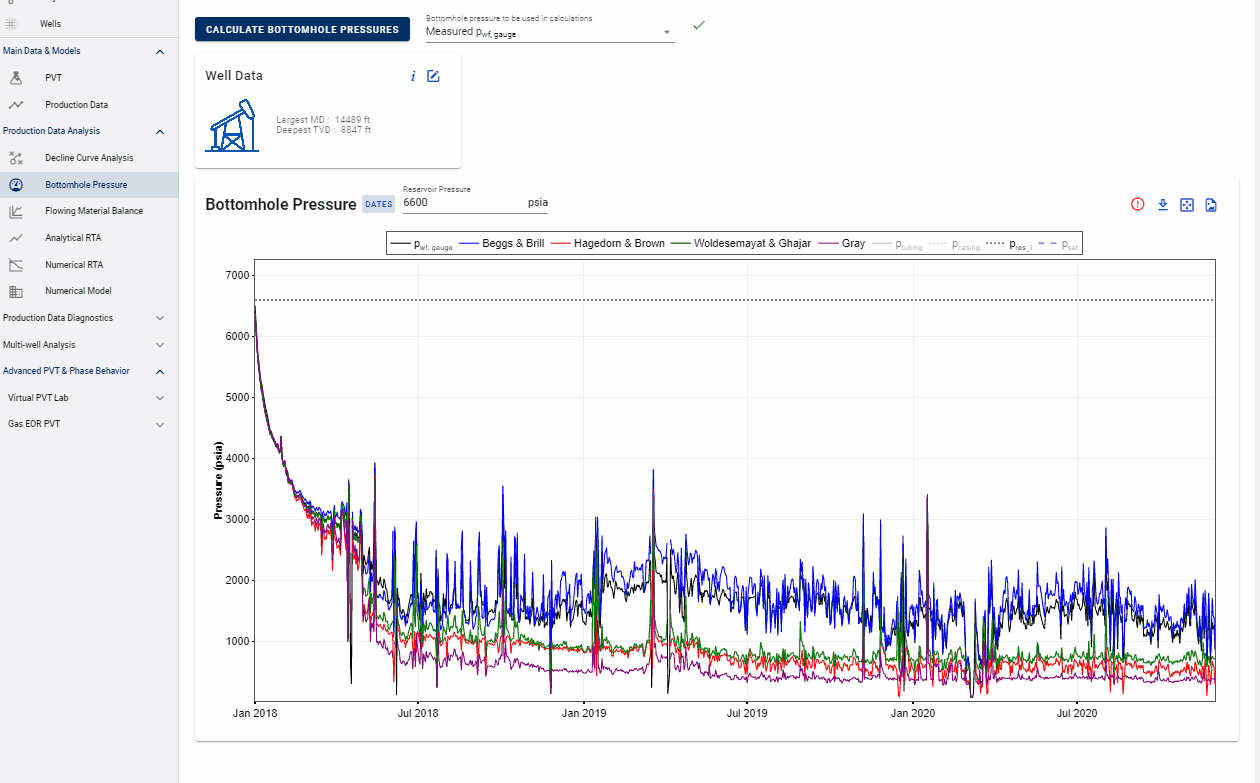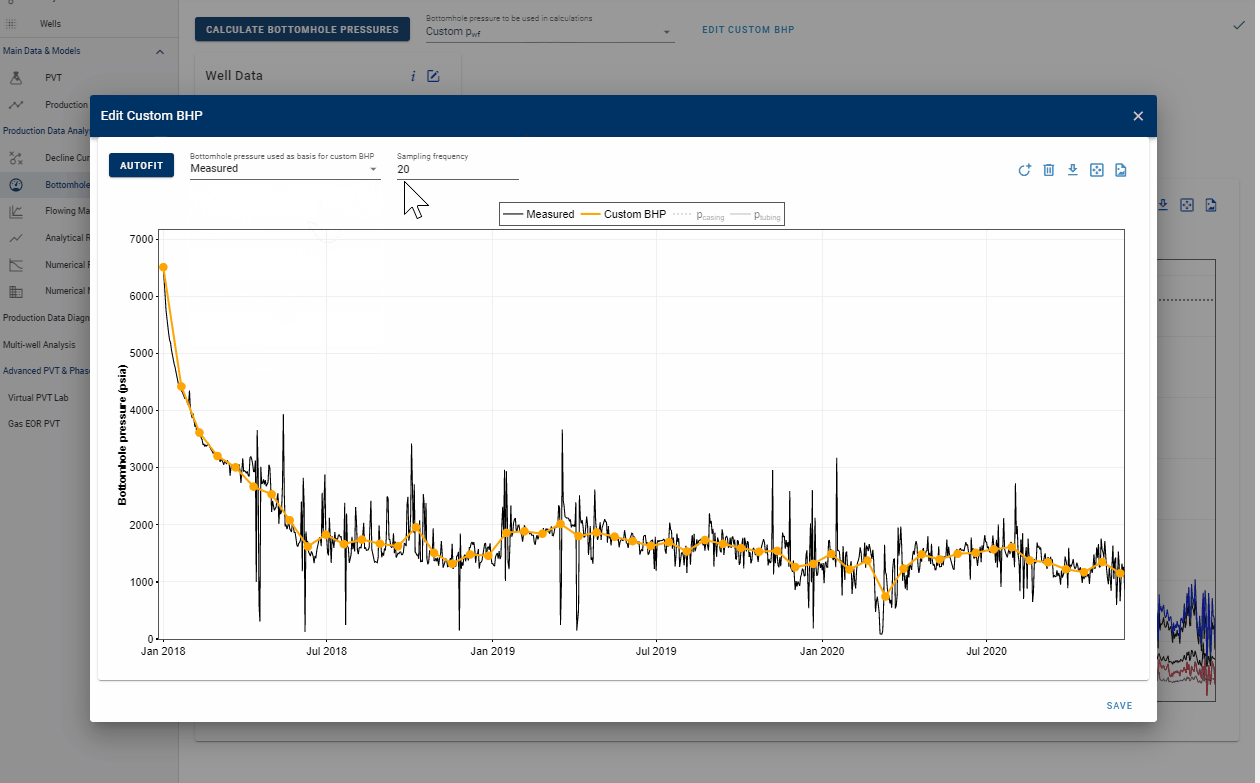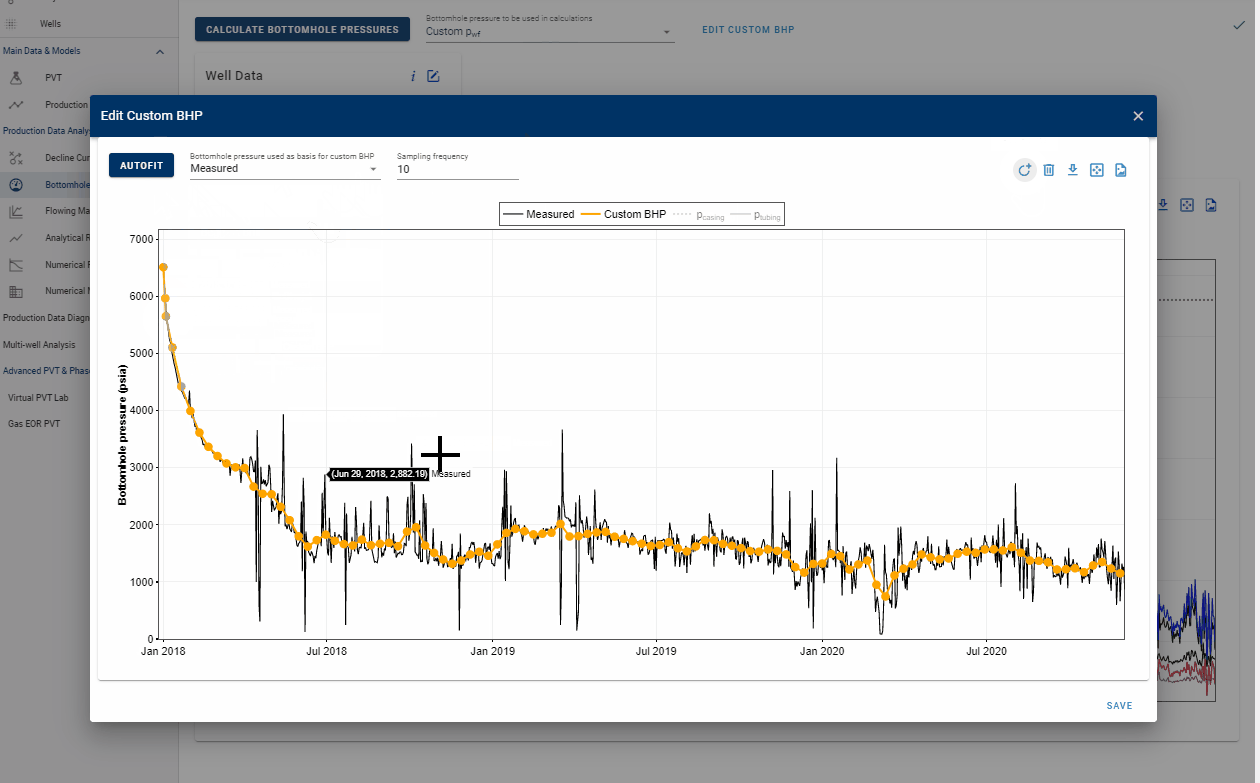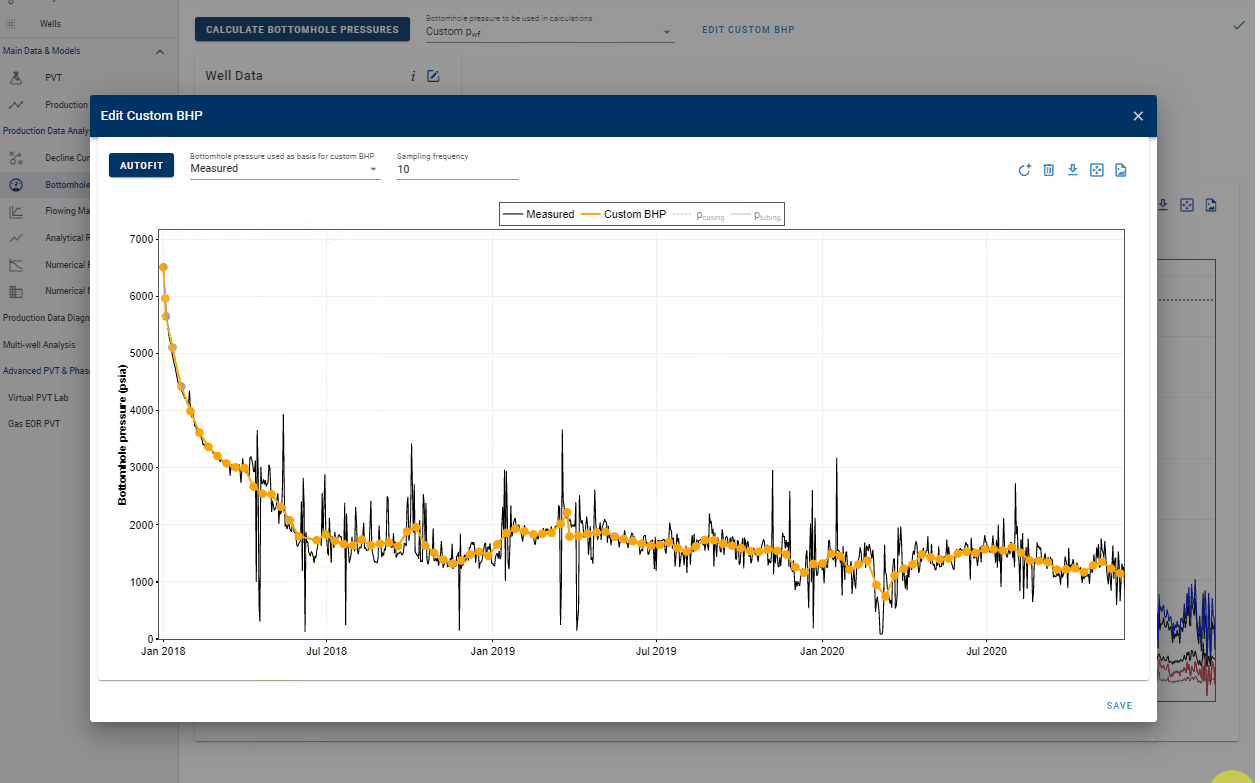
2.2 Custom BHP

Calculated bottomhole pressures are generally noisy due to oscillations in surface rates and pressures. This noise in the bottomhole pressures can have a large impact on the analysis being performed, specially RTA / numerical modeling when the well is controlled on bottomhole pressures. With the custom BHP feature it is possible to piecewise-linearize and smooth the calculated bottomohole pressures. The user can select the sampling frequency and also manually add or remove points from the chart to create the shape / curve that is desired.

2.3 BHP Calculation Stuck?

When the computation takes longer than expected, the user can try to force re-running the calculation as follows:

1. Open Well Data card
2. Click Calculation Options
3. Click refresh icon to Force Run BHP Calculation
4. All steps are shown in the .gif below.

If the problem persists, please contact support@whitson.com

2.4 BHP Plot Options

Show Rates, Surface Pressures

Show Wellbore Configuration Dates

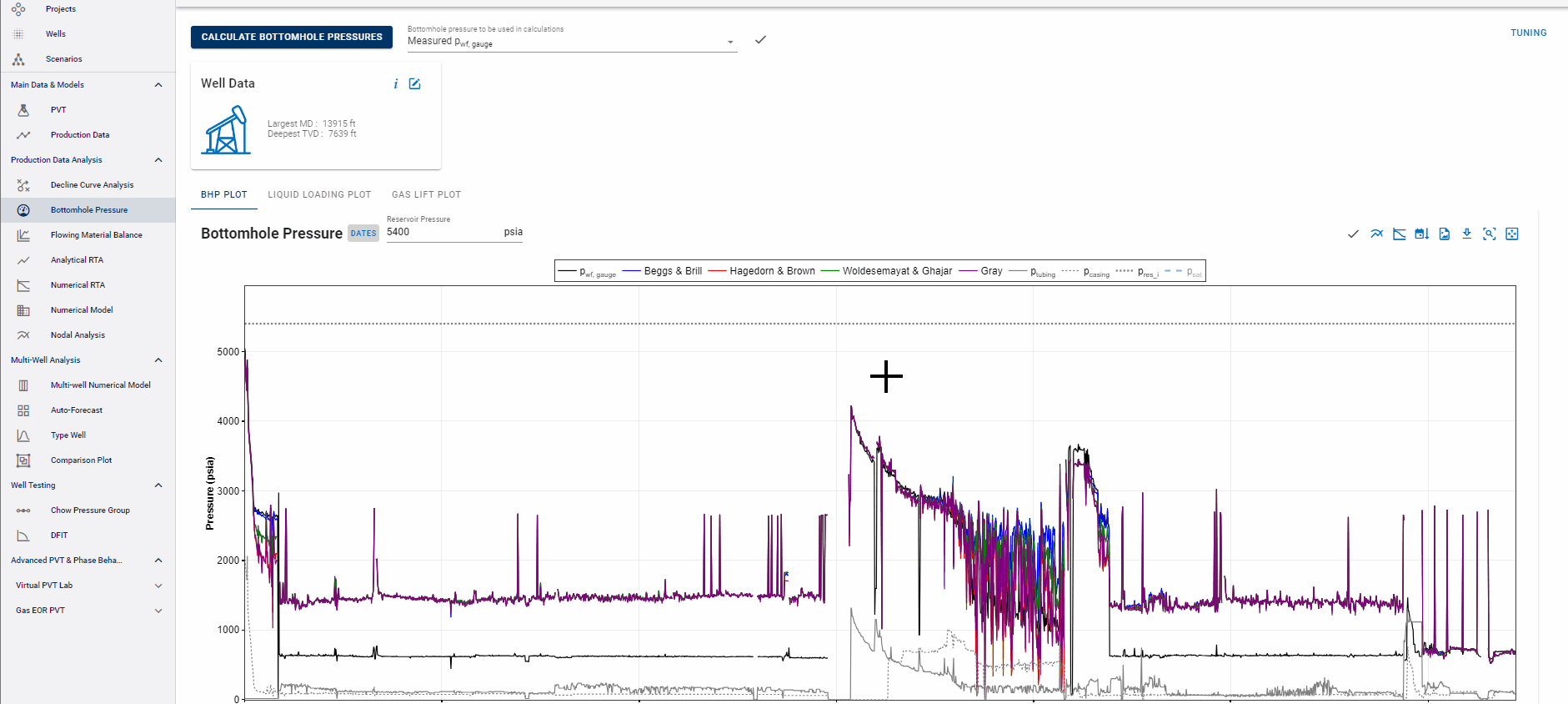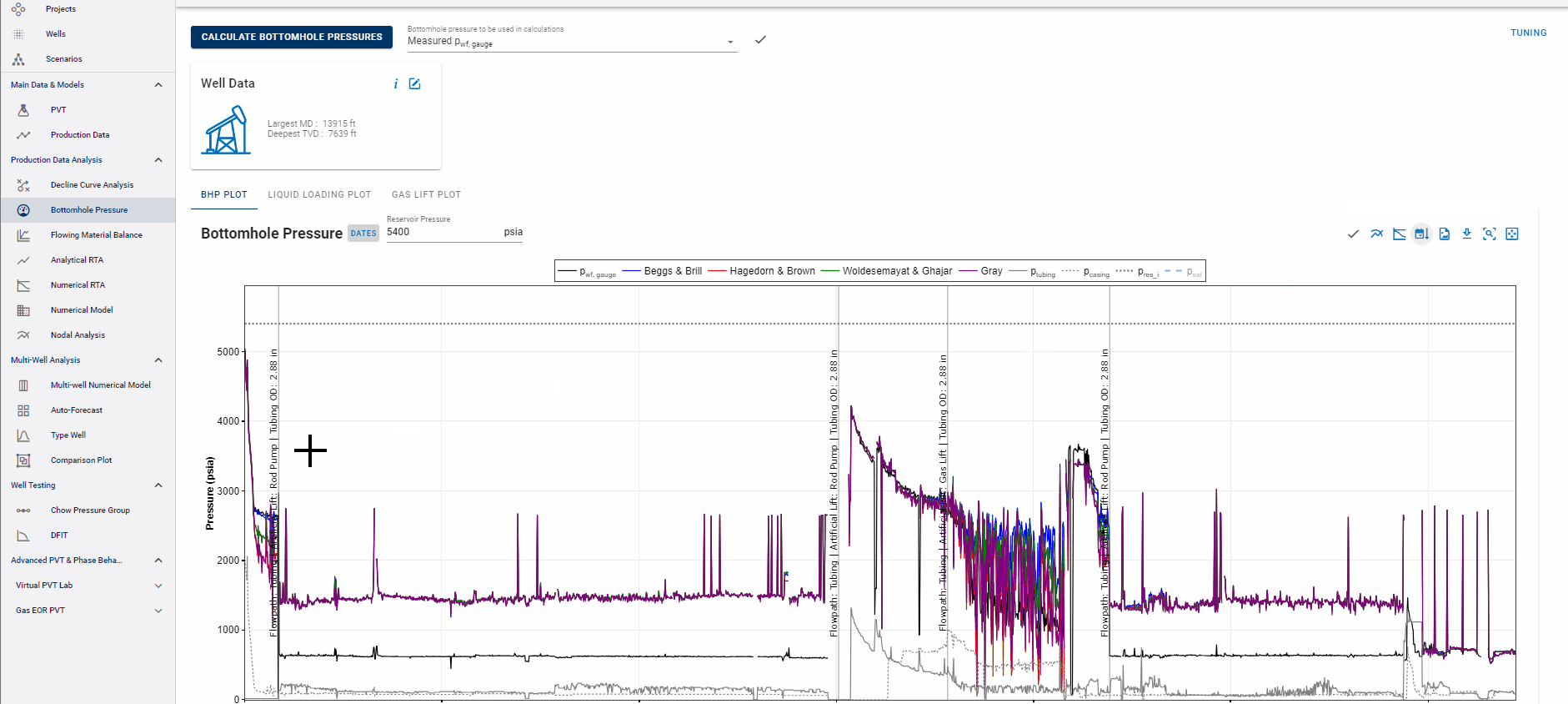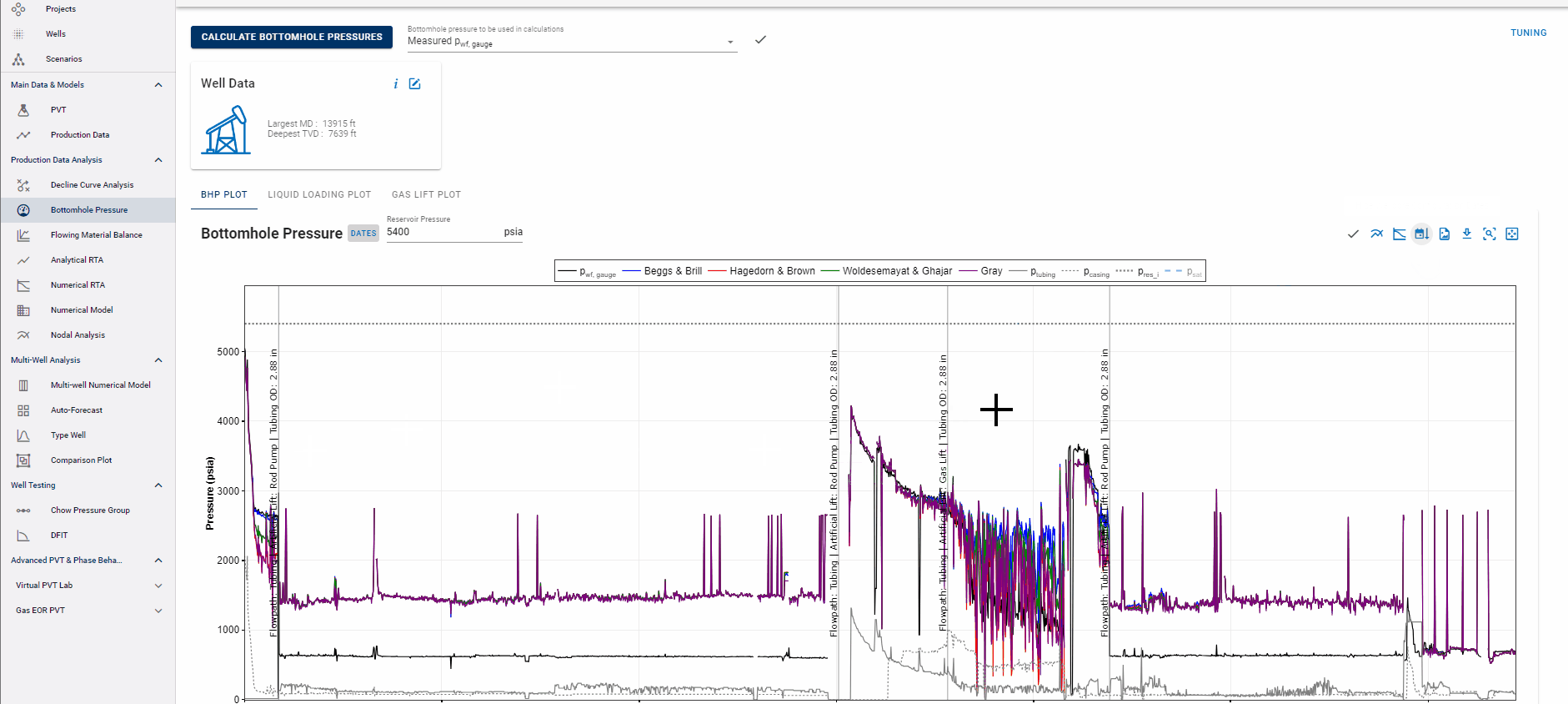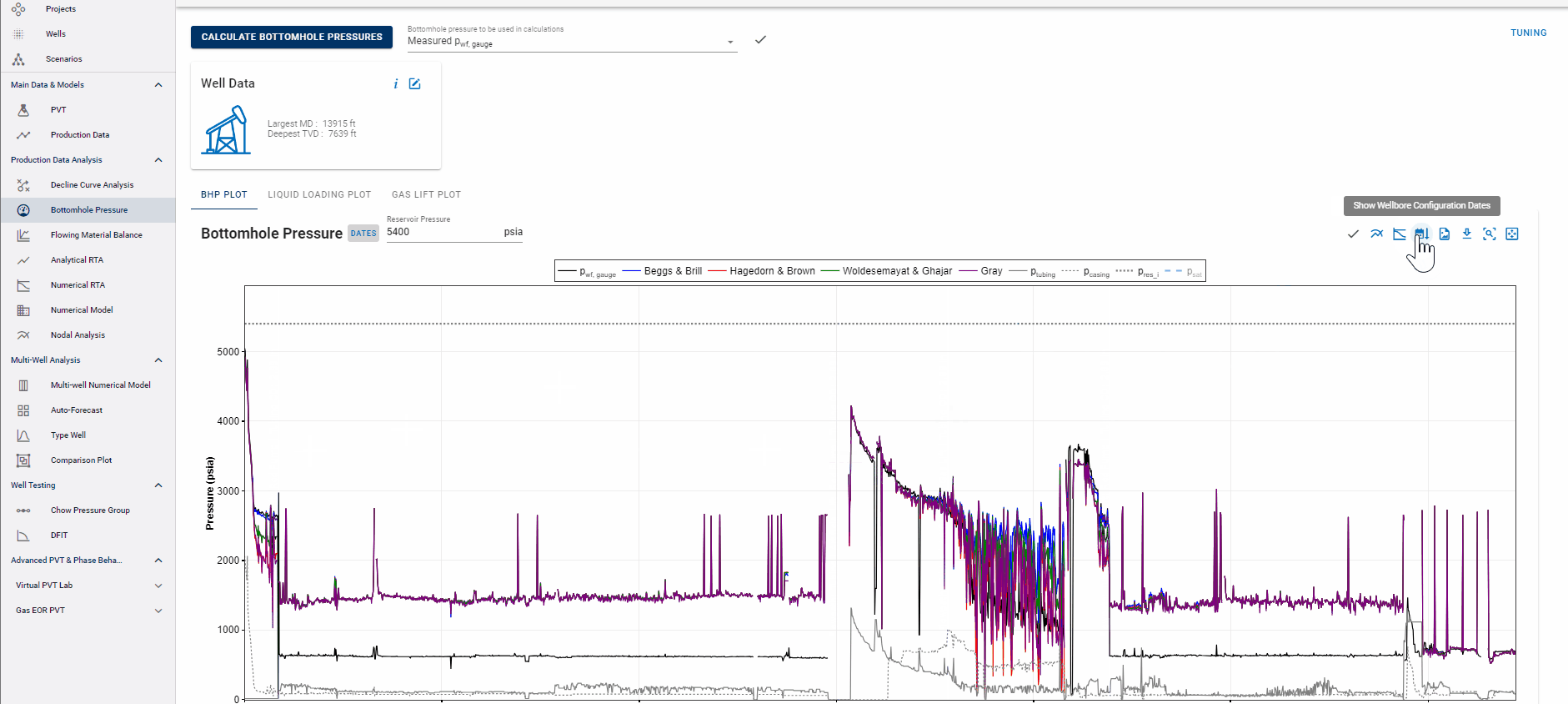
3. Technical Features

3.1 Governing Equations

The main equations used for multiphase flow in inclined pipe are provided here. Our wiki contains a detailed review of the relevant multiphase-flow theory and the commonly used correlations for pipe flow.

$$\begin{equation} -\frac{dp}{ds} = \frac{\rho_gg\cos(\theta)+\frac{f}{2d}\rho_fv_m^2}{1-\frac{\rho_av_mv_{sg}}{p}} \end{equation}$$ $$\begin{equation} T(s) = T_R - \alpha\cos(\theta)\bigg[s+\frac{\dot{m}}{K\pi d}\bigg(\exp\bigg(-\frac{K\pi d}{\dot{m}}s\bigg)-1\bigg)\bigg] \end{equation}$$

3.2 Artifical-Lift Methods

3.2.1 Gas Lift

Gas lift is included as a step change in mass flow at the injection valve. We assume the lift gas to completely mix with the flowing mixture, resulting in a step change in the gas rate, and consequently the producing GOR.

When the well is on gas lift, are gas rates netted or gross (including gas lift rates)?

The inputted gas rates in the production data editor are assumed to be netted out

$$\begin{equation} q_{gas} = q_{gas, flowing total} – q_{gas,injected} \end{equation}$$

The reason we do this is because the gas rate is used everywhere in the system, including numerical model, flowing material balance and RTA; and there the gas lift is not part of the calculation (i.e. not part of the reservoir flow).

In the BHP calculations, to get the total gas that is flowing inside the wellbore, we just do the calculation in the background as follows:

$$\begin{equation} q_{gas, flowing total} = q_{gas} + q_{gas,injected} \end{equation}$$

Three options exist for the gas-lift configuration.

1. Poorboy: The term "poorboy" refers to the situation when injection occurs at the EOT.

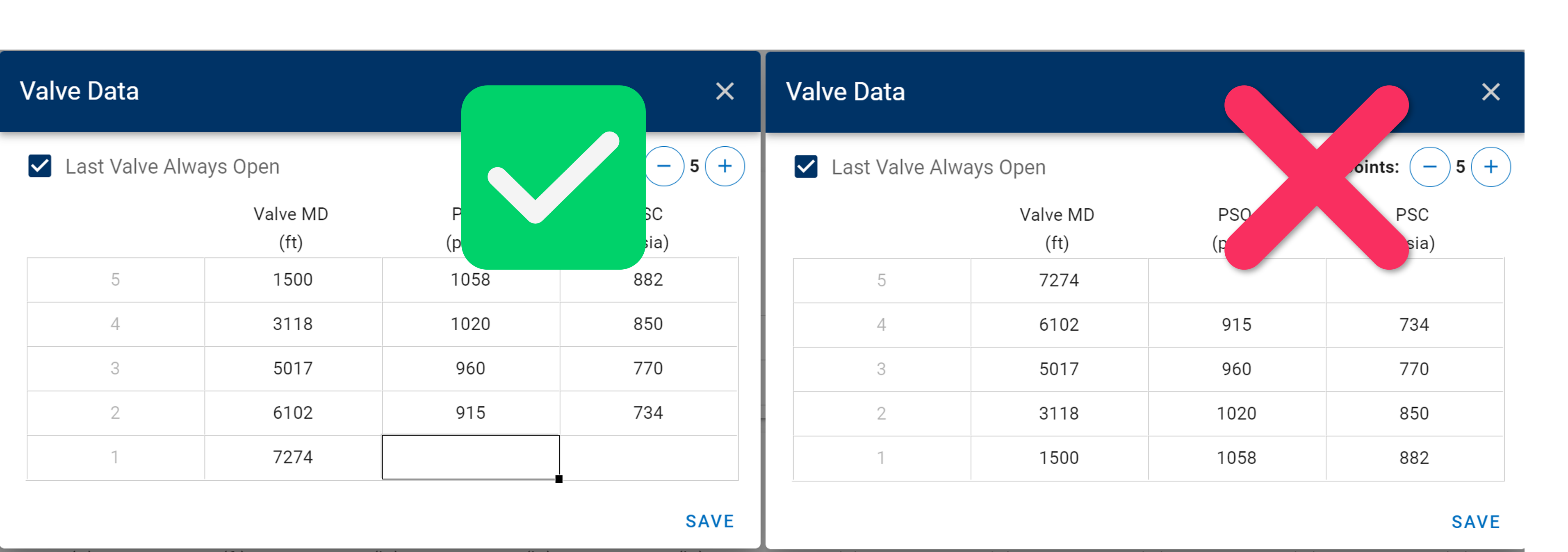
2. Valves: A single valve at a specified depth, or a set of valves at different depths along the tubing, can be provided. If a full set of valves is provided, the casinghead pressure is used to decide which valve the lift-gas enters the tubing through. We assume all of the lift gas to enter the tubing through the first open valve it encounters, even though this rate might exceed the maximum rate predicted by the Thornhill-Craver equation. Note: The gas lift valves are ordered by descending measured depth with valve number. The deepest valve, is valve number 1, the second deepest is valve number 2, and so on. If "Last Valve Always Open" is ticked, then PSC and PSO for valve 1 (if specified) will be disregarded by the calculator.

3. Automatic: If the lift-gas injection depth is unknown, then the BHP calculator can estimate the depth by computing the pressure profiles in the tubing and annulus and finding the depth at which they are equal. If this depth is computed deeper than the EOT depth, then EOT depth is used (poorboy).

If the flow path for a given day is set to "Annulus", a reversed gas-lift configuration is applied where the point of injection is set to be at the deepest valve if there is only a single valve depth specified or "Last Valve Always Open" is ticked for a set of valves. If not, the lift-gas is injected at the EOT.

Which gas lift configuration to choose for a given well?

Is there a packer in the well? If so, it is likely that the gas lift configuration uses valves, meaning that the injected gas enters through valves in the tubing. In this case the depth of the valve(s) that allow gas to flow from annulus to tubing (or viceversa) is a required input.

If packers are in the hole, but the valve depth is unknown, then picking the “Automatic” gas lift configuration is the best choice, then the BHP calculator can estimate the depth by computing the pressure profiles in the tubing and annulus and finding the depth at which they are equal (that would be the injection depth). One important consideration is that using "Automatic" gas lift configuration in this case might lead to the injection happening at end of tubing (EOT), which would not be consistent with having a packer in the whole, but this will only occur if the depth is computed to be deeper than EOT based on the input data.

If there is no packer installed in the hole, there is communication between annulus and tubing through the end-of-tubing (EOT) and therefore the appropriate gas lift configuration is “Poor-boy”.

Differences in Gas Lift Configurations

• Gas Lift configuration "Valves" are assumed to open in the direction Annulus->Tubing (conventional logic). This means that when lift-gas is injected into the annulus (flowpath=Tubing), the lift-gas will enter the first valve that opens based on the casinghead pressure (CHP). If the lift-gas is injected into the tubing (flowpath=Annulus), then only the last valve may permit the gas going through if "Last Valve Always Open" is ticked. Otherwise, the lift-gas will go down to EOT and enter the wellstream there (poorboy). Gas lift valves are one-way valves, with the exception that the last (deepest) valve may just be an orifice (just an open hole), we allow for this by having the "Last Valve Always Open" tick box.

• Gas Lift configuration "Reversed Valves" results in the opposite logic, because all the gas lift valves are opening in the direction Tubing->Annulus.

Flowpath	Gas Lift Configuration	Lift Gas is Injected Into	Lift Gas enters Wellstream at
Tubing	Poorboy	Annulus	EOT
Annulus	Poorboy	Tubing	EOT
Tubing	Valves	Annulus	First Open Valve
Annulus	Valves	Tubing	Last Valve if "Last Valve Always Open", else EOT
Tubing	Reversed Valves	Annulus	Last Valve if "Last Valve Always Open", else EOT
Annulus	Reversed Valves	Tubing	First Open Valve

When using "Unknown" flowpath, the Gas Lift Valve direction is important. This is because the same gas lift well configuration can be used while swapping the flow path between Tubing and Annulus by the maximum wellhead pressure between CHP and THP.

3.2.2 Rod Pump

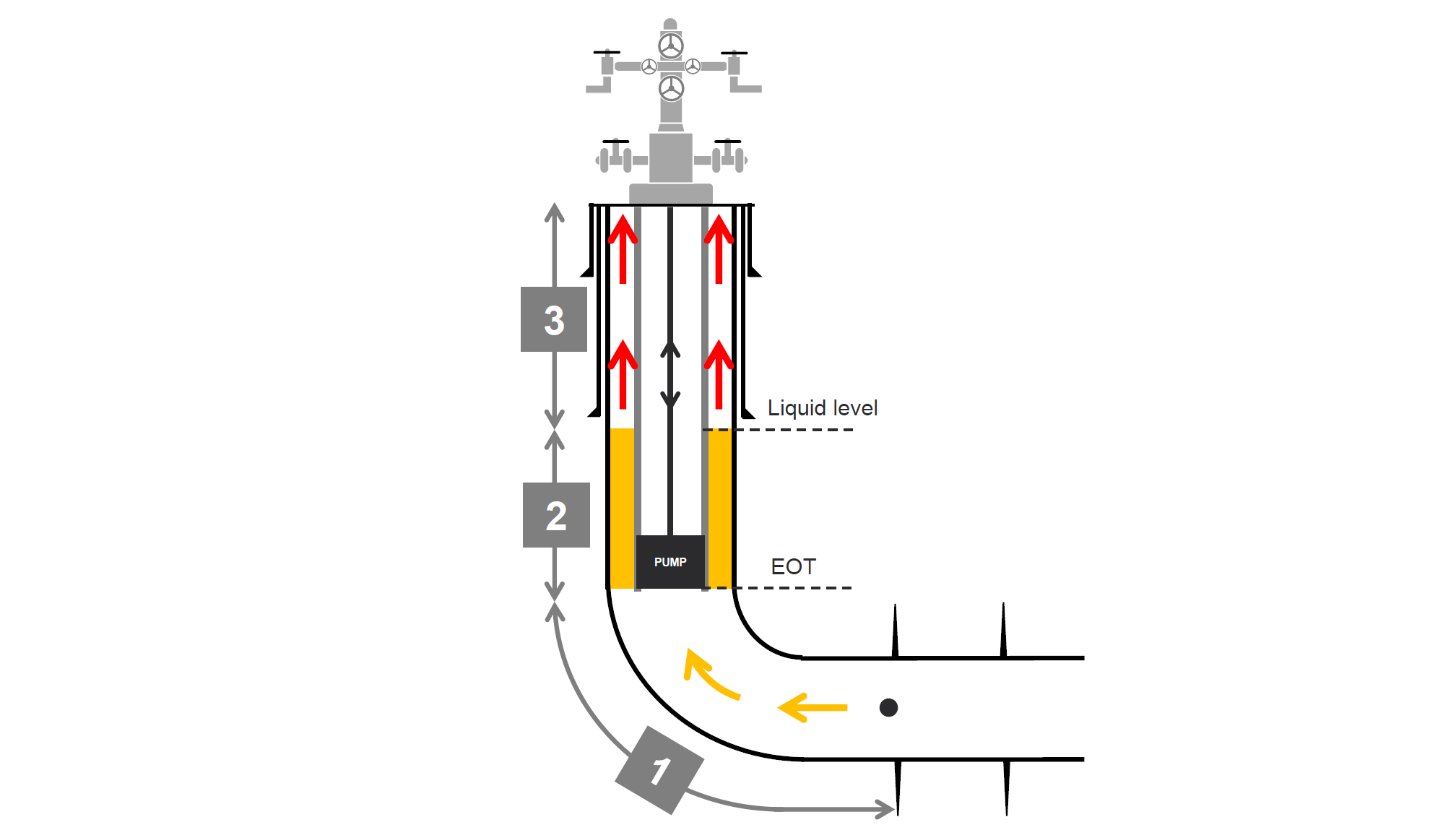
BHP calculations with a rod pump are achieved by dividing the well into three parts:

1. Top Perforation to Inlet of Pump (EOT)—Full wellstream flowing in production casing, regular multiphase pipe flow.

2. Inlet of Pump (EOT) to Liquid Level in Annulus—Static liquid column with gas bubbles percolating through it.

3. Liquid Level in Annulus to Wellhead—Single-phase gas flow in the annulus. The gas that has percolated through the liquid column flows to the wellhead.

We assume the fluid split at the inlet of the pump to be such that all surface gas goes through the annulus, and all liquid goes through the pump and up the tubing. This is an approximation of the true split, and thus the estimated BHP may be somewhat larger than the true solution (less gas goes through the annulus in real life than what is modeled).

Most of the pressure drop for rod pump occurs in the second part, (i.e., the static column of fluid) as this is most-often along the vertical part of the well where the gravity pressure drop dominates. This fluid column will in most cases be liquid-like where the liquid is stagnant and the produced gas is percolating/rising through the liquid as bubbles. A new model to honor this liquid-like fluid column has been introduced to the rod-pump calculations, as the original model was overly sensitive to gas rate and consequently predicted too low pressure drop in the fluid column.

Why can't I select between flowing side or static (quiet) side when artifical lift is set to rod pump?

Casing pressures are always used as a pressure source for rod pumps, ignoring tubing pressures. Therefore, it is always a static (quiet) side calculation, and hence there is no option to choose between flowing and static (quiet) side.

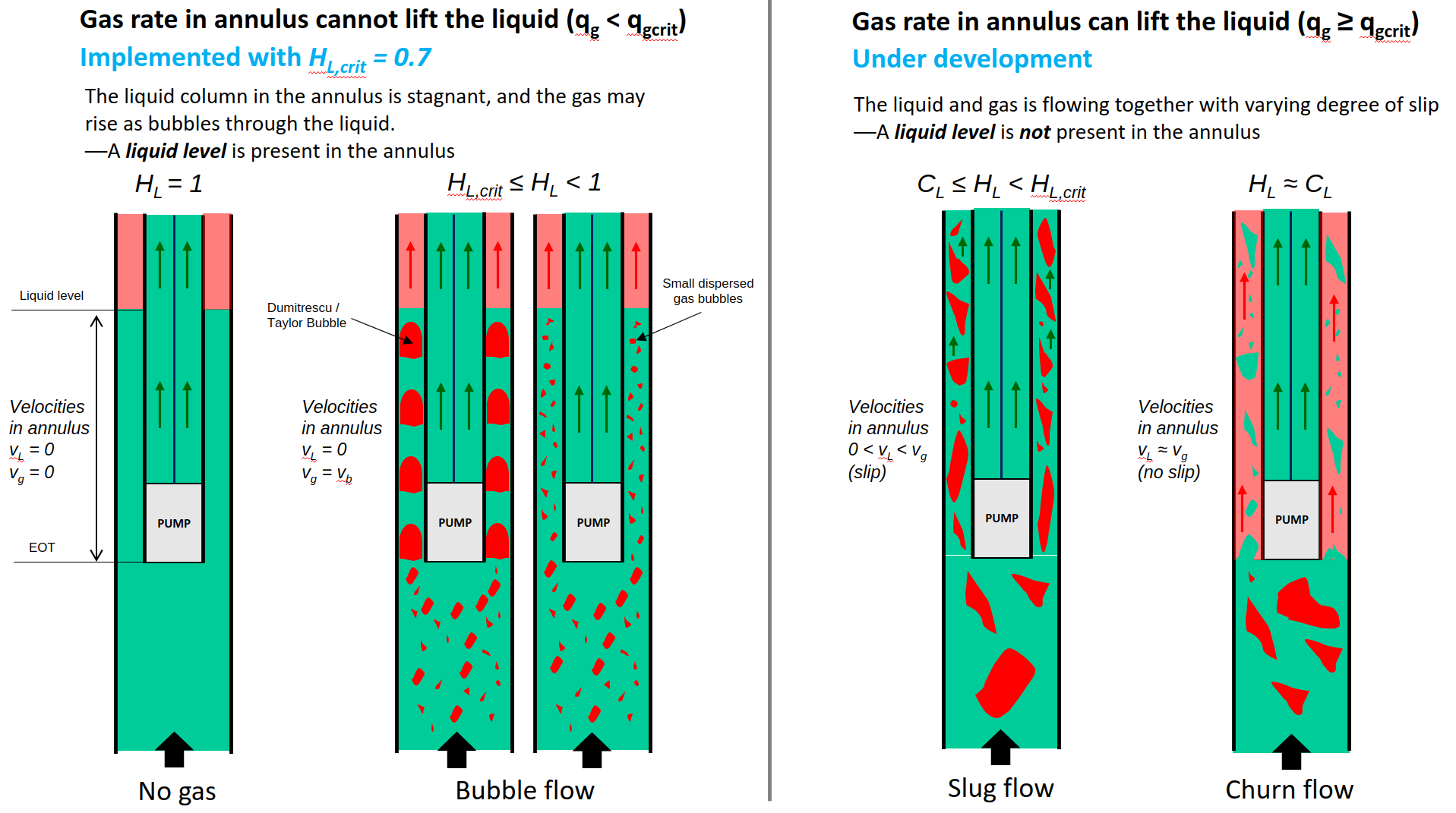
The figure below show four flow regimes/modes for rod pump.

• The flow regimes to the left represents the situation when the gas is not able to carry the liquid with it, causing a well-defined liquid level in the annulus. This model has been implemented, with a critical liquid hold-up set to 0.7.

• The flow regimes on the right represents the situation when the gas is able to carry liquid with it. This is not implemented yet.

Unifying the left and right flow modes requires (1) a method of estimating the critical liquid hold-up (i.e., the transition between left and right models), and (2) a method of estimating the fraction of the total produced liquids that goes up the annulus. This is under development.

3.2.3 Plunger Lift

Plunger lift is a method of artificial lift that uses a free piston traveling up and down inside the tubing in a cyclic manner. When traveling up, the piston removes accumulated liquids from the wellbore which reduces flowing bottom-hole pressure and increases flow rates for a period. When there is liquid accumulation again, the well is shut-in, the piston travels down and the process is repeated.

Sketch by Milan Stanko

Plunger lift stages:

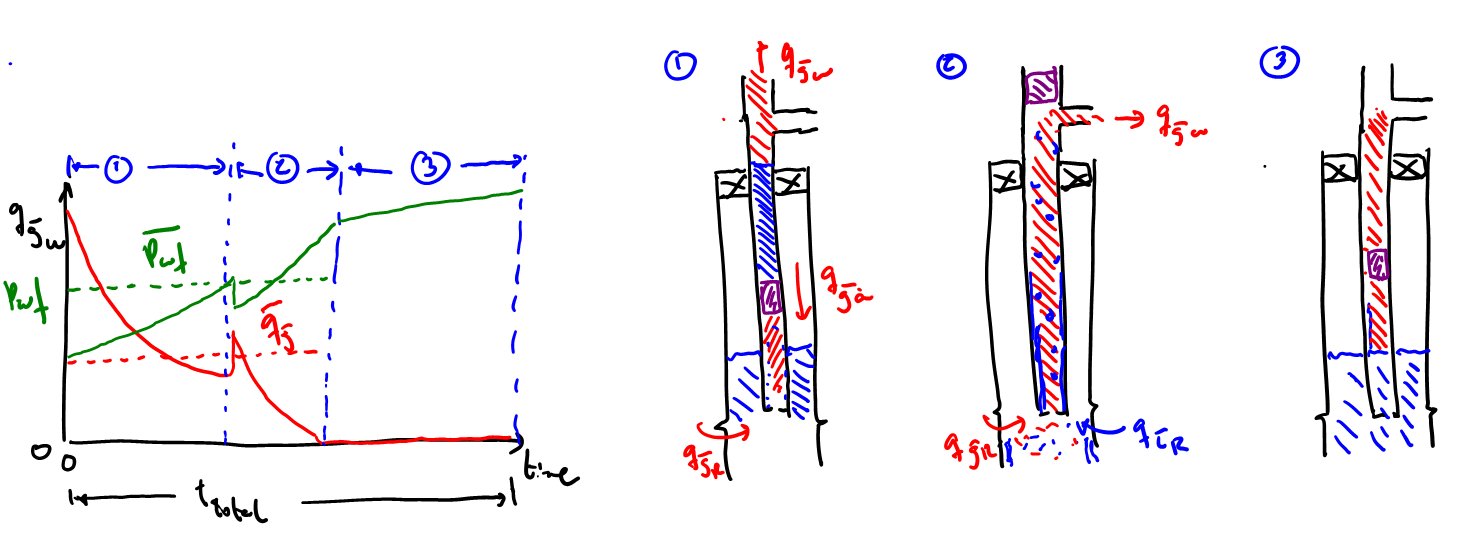
Stage 1. After the well is opened, the plunger is pushed upwards by the gas in the near wellbore and the gas in the casing (in case there is no bottom-packer). The average velocity of the plunger might be something in the vicinity of 5-10 m/s (higher at the beginning of the cycle and slower later). For a 3000 m deep well this means it takes between 5-10 min to reach the top of the well. During this stage, all the gas that is above the liquid slug pushed by the plunger is produced (and maybe some gas bypasses the plunger and liquid slug).

Stage 2. The plunger reaches the top and is parked. The gas flowing behind is deviated to a bypass line, which is usually accompanied by a modest increase in the gas rate, since it doesn't have to push plunger and liquid slug any longer, it is flowing through unobstructed pipe and the wellbore is liquids free. For the rest of stage 2, reservoir gas and liquid enter the wellbore. Most of the liquid stays behind being accumulated at the bottom of the well. The duration of this stage is usually short (maybe a few minutes), because the liquid fills up the tubing quite quickly, but it depends on the LGR of the well and size of tubing and casing.

Stage 3. The well is shut in, liquids accumulate at the bottom, the plunger is dropped and travels to the bottom of the tubing. Velocity of the plunger is maybe 5 m/s or less (specially when passing through the liquid), so it takes also like 10 min to reach the bottom. After that the cycle is initiated again.

Quote

"To the left of the figure above I have sketched (in solid red color) the well gas rate in the 3 stages, and the flowing bottom-hole pressure (in solid green). The well gas rate is measured and reported, but the BHP is my speculation "back calculated" from IPR (BUT during stage 1 BHP depends on the force balance on the plunger, how much fluids are coming from casing, how much from formation, etc.)." Milan Stanko

When a well is operating on plunger lift, the wellbore flow is constantly going through short flow transients due to the cyclical nature of plunger lift operation. To calculate bottomhole pressure in these cases would require a small time scale simulation of the transient process and that would be outside the scope of what we normally want to do for practical petroleum engineering applications. However, it is still possible to calculate an average steady-state bottomhole pressure for plunger lifted wells as follows:

Option 1. If liquid level is measured in the annulus, provide a liquid level together with the production data. Make sure the liquid levels input correspond to times when the well is producing. This method is similar to how BHP is calculated for rod pump wells when liquid levels are available.

Option 2. Calculate the bottomhole pressures as if plunger was not installed by using the average rates of a producing time period. To capture the effect of less liquid in the tubing during the production period, it is also possible to reduce the OGR of the well. This option consists of:

• Find an average \(q_{g-well}\) for the producing plunger lift stages (1 and 2). This requires the daily production rate (\(q_{g-daily}\)), the producing cycle duration (\(t_{prod}\)) and number of cycles in a day (\(N_{cycles}\)).

$$\begin{equation} q_{g-well}=\frac{q_{g-daily}*24*60}{N_{cycles}*t_{prod}} \end{equation}$$

• Run a BHP calculation using the average \(q_{g-well}\) and neglecting most liquid (e.g. assume fry gas, mist flow)

The average \(q_{g-well}\) and BHP for cycle 1 and 2 are illustrated in the figure above in dashed red and green line, respectively.

Why can't I select between flowing side or static (quiet) side when artifical lift is set to plunger lift?

Casing pressures are always used as a pressure source for rod pumps, ignoring tubing pressures. Therefore, it is always a static (quiet) side calculation, and hence there is no option to choose between flowing and static (quiet) side.

3.2.3 Gas-Assisted Plunger Lift (GAPL) and Plunger-Assisted Gas Lift (PAGL)

GAPL vs PAGL - What's the Difference?

Many people use these terms interchangeably to refer to combinations of gas-lift and plunger-lift. While we know of no formal SPE definition, we use GAPL to refer to gas-assisted plunger-lift, and PAGL to refer to plunger-assisted gas-lift.

From this perspective, PAGL and GAPL may occur at two different stages in the well's life cycle.

In each scenario, one type of lift supports another primary lift method:

PAGL: The plunger enhances and prolongs the economic viability of the gas-lift system by enhancing efficiency and economics at lower rates. This extends the operational period of the gas lift system toward the end of the life cycle before transitioning to another lift method.

GAPL: Gas injection boosts and extends the economic life of the plunger-lift system by complementing the reservoir drive. This extends the operational period of the plunger-lift system toward the end of the life cycle before transitioning to another lift method.

Another way to conceptualize the distinction, in most cases, is:

PAGL: Continuous gas-lift supported by a continuous-run plunger. GAPL: Plunger-lift supported by continuous or intermittent gas injection.

While both PAGL and GAPL, when appropriately applied, can enhance production over using a single lift method, they represent distinct lift approaches that can be strategically incorporated into the well's life cycle planning. By designing the well to anticipate these changes and minimize workover costs, one can optimize production and economic efficiency.

How Calculate BHPs for GAPL/PAGL systems?

As of now, it is not possible to input more than one artificial lift in whitson+ at the same time. However, in case of GAPL/PAGL, we suggest to Use option 2 + Gas lift as artificial lift. under the Plunger Lift category above. Option 2 suggests to calculate BHP as if plunger lift was not installed, then use gas lift and account for the valve depth. Gas lift does not change any of the plunger lift mechanism. The only difference is that there is a bottom-packer, gas in stage 1 comes from reservoir only. With Gas lift there is a bottom packer that disconnects liquid level from the BHP.

3.2.5 Jet Pump

A jet pump consists of four static parts: nozzle, throat inlet, throat and diffuser. Highly pressurized power fluid is converted to kinetic energy through the nozzle. Reservoir fluid, with a much lower pressure, is accelerated into the throat. The fluids are mixed in the throat and a homogeneous mixture is developed at the diffuser inlet. The kinetic energy of the mixed fluids is converted to pressure energy in the diffuser. This pressure increase across the pump is what lifts the mixture to the surface.

It is not possible to calculate bottomhole pressures in whitson+ when the wellbore has a jet pump installed. Jet pumps are one of the most difficult pumps to model for hydraulic calculations, and a lot of the information needed to make the calculation is proprietary of the owner of the pump. That is why most pump suppliers have their own software for modeling hydraulics with jet pumps.

In addition to the geometrical configuration and size of the different jet pump components, the most important jet pump parameters that are generally held confidentially by the jet pump supplier are the loss coefficients:

• Nozzle loss coefficient
• Suction loss coefficient
• Throat loss coefficient
• Diffuser loss coefficient

Recommendation for Well with Jet Pump. It is possible to have a bottomhole pressure gauge installed while operating with jet pump, and that is the best way to estimate the flowing bottomhole pressure in such cases. An alternative to finding the correct bottomhole pressures for a period with jetpump is to use the custom pwf feature in whitson+, and “draw” a pressure profile in the jet pump period that is more aligned with an expected pwf decline for the given well. This exercise is even better if you have pwf before and after the jet pump was installed, so we are confident in the limits of the interval (and the drawing is not just a shot in the dark).

3.2.6 ESP

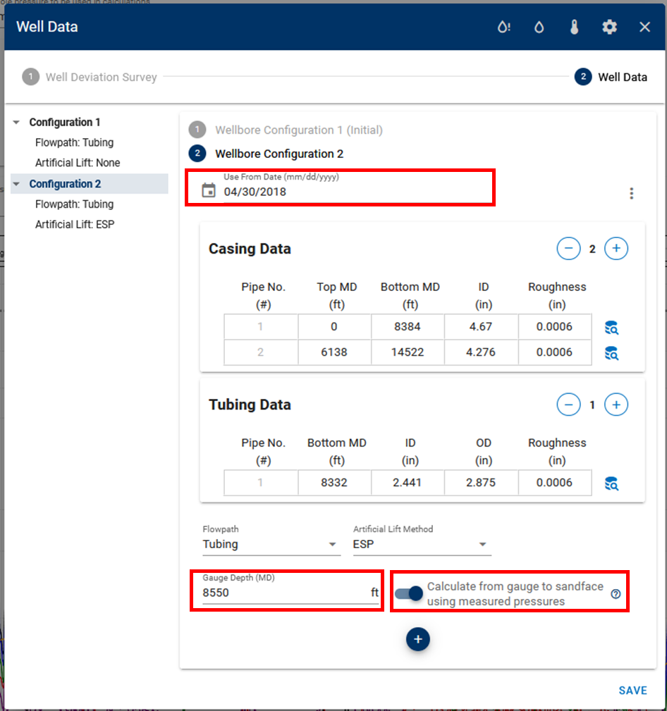
To set up a well with ESP, mainly, you want to ensure the following -

1. Your inlet pressures are loaded into the Gauge Pressure (p_{wf, gauge}) column,
   
2. Your wellbore configuration is loaded with the change in wellbore configuration from previous to ESP at the right 'Use From Date'.
   
3. Your wellbore configuration with ESP has a pump intake depth and 'Calculate from gauge to sandface using measured pressures' turned on.
   This computes the bottomhole pressure drop from the pump inlet to the top perforation
   - assuming the loaded gauge pressures record the pump intake pressures.
   

Finally, if everything like the pressure production data, looks okay and the pump is sized appropriately, the bottomhole pressure should show a smooth transition from previous wellbore configurations to flowing via ESP.
Be sure to not use these bottomhole pressures for tuning the correlations, this is why.

3.3 Dual-Conduit Flow

If the flow path is set to "Tubing and Annulus", the BHP is calculated by allowing the wellstream to flow in through both annulus and tubing. The split of flow must be solved for by requiring that the pressure at the end of tubing is the same when calculating the pressure drop through both conduits, starting with casinghead pressure for the annulur flow, and tubinghead pressure for the tubing flow.

3.4 Liquid Loading

3.4.1 Classical Critical-Rate Correlations

The Tuner[1] and Coleman[2] critical rates are the classical correlations of predicting the minimum required gas rate to avoid liquid loading. These correlations can be used at all depths along the well. The correlations rely on a force balance on a liquid droplet to predict the minimum velocity needed to lift the droplet. The only difference between the two correlations is that Turner is 1.2 times Coleman.

The equation for the Coleman critical velocity is

$$\begin{equation} v_{c} = C \bigg(\frac{\sigma_{Lg}(\rho_L-\rho_g)}{\rho_g^2}\bigg)^{1/4} \end{equation}$$ where \(C\) is a unit conversion factor (1.5935... in field units), \(\sigma_{Lg}\) is the liquid-gas IFT, \(\rho_L\) is the liquid density and \(\rho_g\) is the gas density.

Converting the velocity to rate is done by $$\begin{equation} \label{eq:rate} q_{c} = v_c A_h / B_g \end{equation}$$ where \(A_h\) is the hydraulic area and \(B_g\) is the gas formation volume factor.

3.4.2 Critical-Rate Correlations Accounting for Well Inclination

A modication to the Coleman critical velocity was made by Belfroid[3] to account for the well inclination. This is useful if the critical rate is computed at a different depth than the wellhead. The modified velocity is $$\begin{equation} \hat{v}_c = v_c\sin^{0.38}\bigg(1.7\bigg(\frac{\pi}{2}-\theta\bigg)\bigg)\frac{1}{0.74} \end{equation}$$ where \(\theta\) is the inclination (deviation from vertical).

Note

The correction could be applied to both the Turner and Coleman critical velocities. In whitson⁺, Belfroid refers to the modified Coleman critical velocity/rate.

Nagoo[4] suggested a different correlation entirely $$\begin{equation} \tilde{v}_c = C \frac{\rho_{L}-\rho_g}{\sqrt{\rho_g\sigma_{Lg}}}\cdot g\cos(\theta)\cdot d_h^{3/2} \end{equation}$$ where C is a unit conversion factor (0.53244... in field units). Both these velocities are converted to rate using Eq. (\ref{eq:rate})

3.4.3 Identifying Liquid Loading in whitson⁺ using Critial Rate Correlations

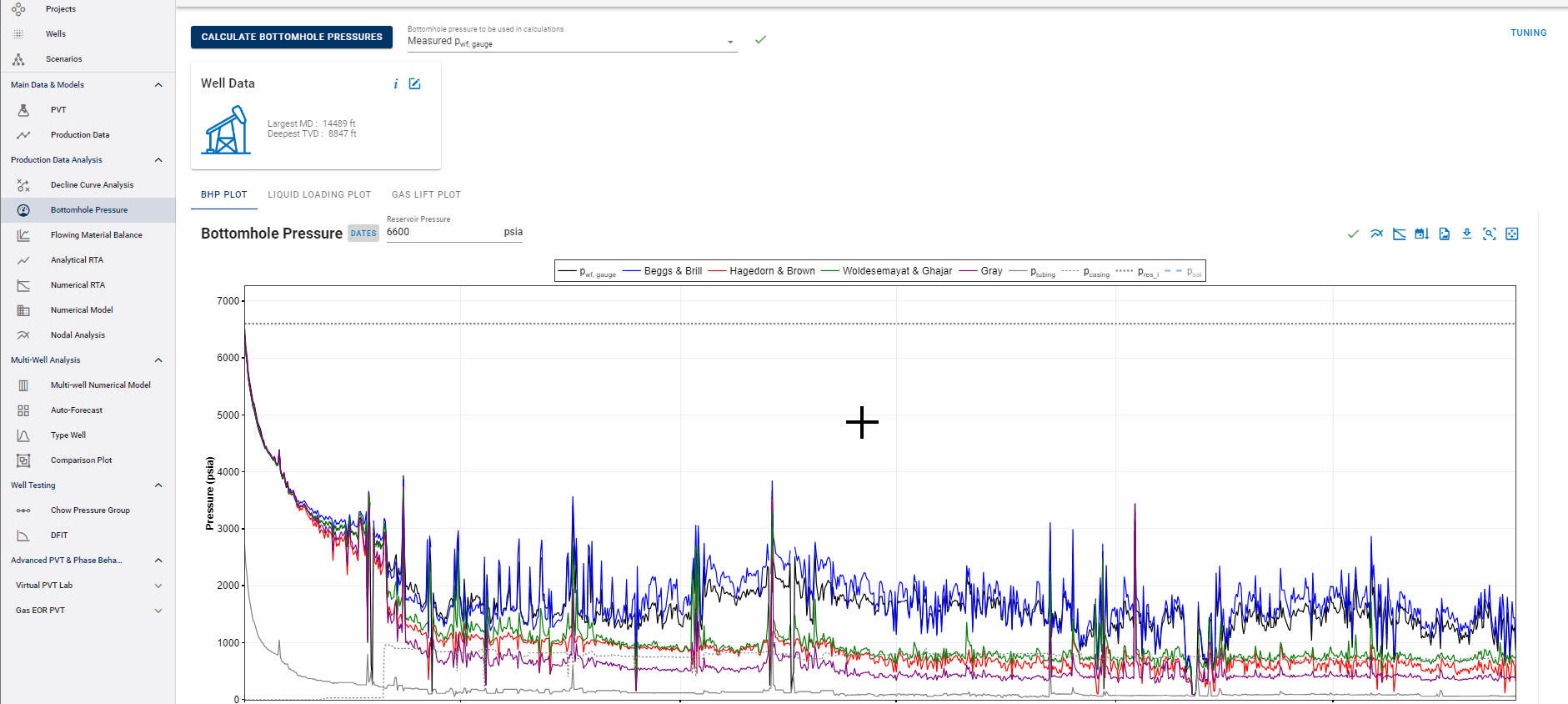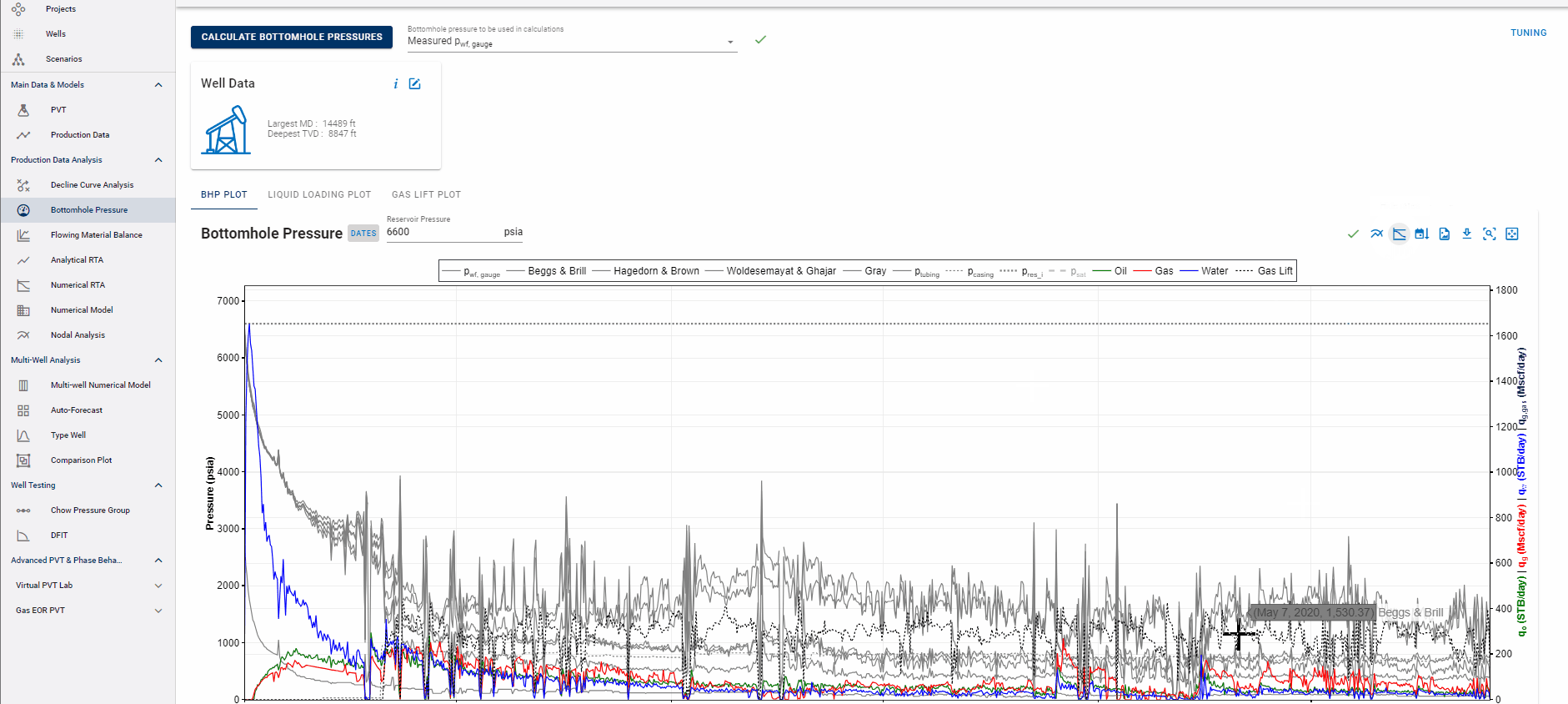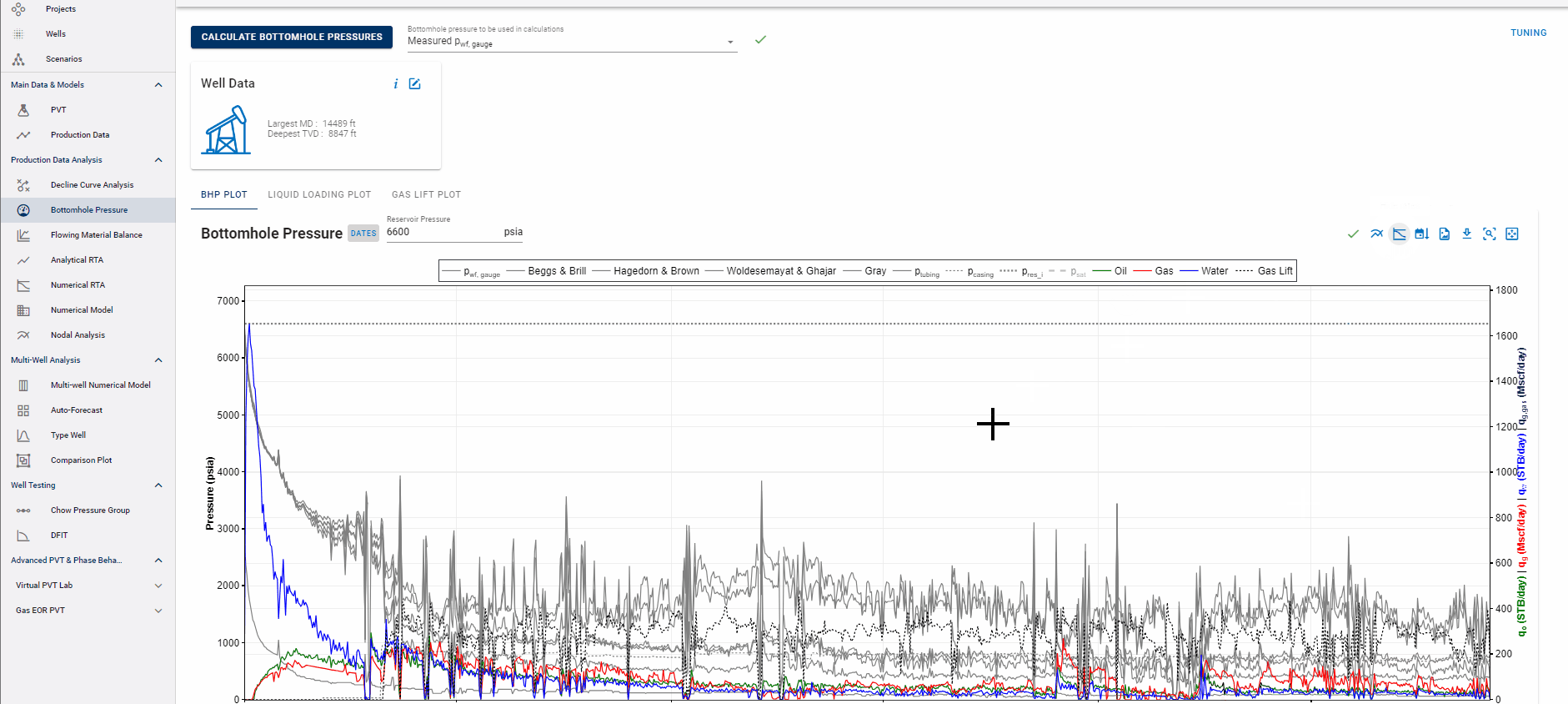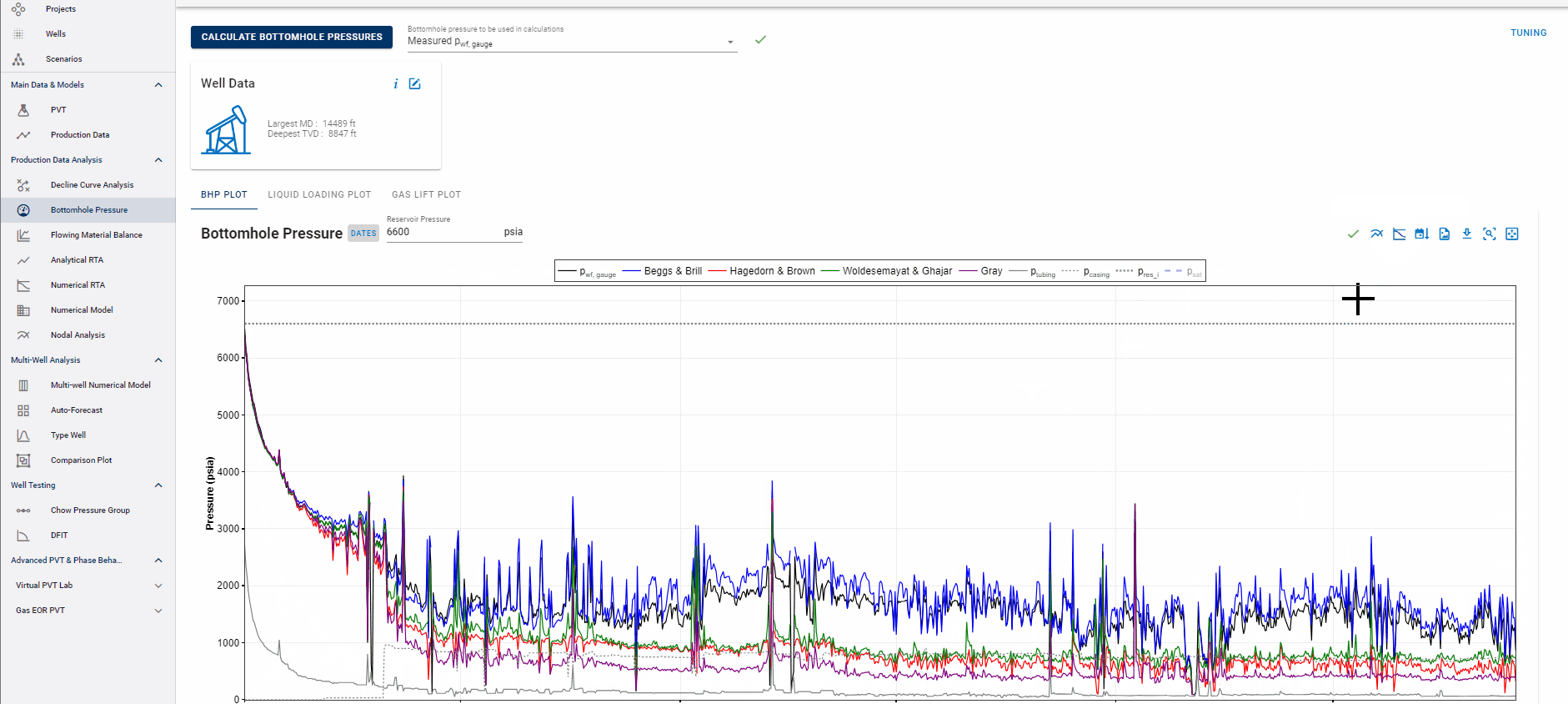
You can use the critical rate correlations above to see if the well is liquid loaded in the BHP feature itself.

Click on the 'Liquid Loading' tab in the BHP feature and choose the following:

1. Critical Rate Correlation: to calculate and plot the minimum required gas rate required at the critical rate depth to avoid liquid loading. Choose between Turner, Coleman, Nagoo and Belfroid - the plot should update with the chosen correlation. You can switch between these, without having to recalculate BHP if these are already calculated once.
2. Critical Rate Depth Type: Depth at which this correlation is used to calculate critical rate. Ensure that the BHP is calculated at least once and every time the critical rate depth is changed, to ensure the critical rate is recomputed for the right depth. Default critical rate depth, for consistency, is 'End of Tubing' for all wells. For wells without tubing in the wellbore configuration, the default critical rate depth will be 'Top Perforation' instead.

Why is the default critical rate depth 'End of Tubing'?

Within the tubing, the pressure is highest at the End of Tubing (EOT), and therefore the gas velocity is the lowest at the EOT. This is the location, within the tubing, we are most at risk for liquid loading. In short, if we are able to lift liquids at the EOT, we are guaranteed to lift liquids at every depth above the EOT in the tubing, due to the pressure decreasing and the gas velocity speeding up. Alternatively, we may be above the critical lift rate at the surface, but that tells us nothing about whether we're liquid loaded deeper in the wellbore.

Ensure that the BHP is calculated at least once and an appropriate 'Bottomhole Pressure to be used in calculations' is also chosen because the critical rates will change accordingly. You need to strictly use one of the correlations for calculating critial rates so if you have 'Measured p_{wf, gauge}' or 'Custom p_wf' selected in 'Bottomhole Pressure to be used in calculations', they will default to Hagedorn and Brown.

Critical Rates can be calculated for the following critical rate depth types:

1. Wellhead - Critical rate is computed at the wellhead, i.e. at surface (depth of 0 ft).
2. Top Perforation - Default, if tubing is absent - Critical rate is computed at the top perforation depth (as entered in the well data card).
3. End of Tubing - Default, if tubing is present - critical rate is computed at the end of tubing, i.e. at the tubing intake (as per the wellbore configuration).
4. Maximum Rate - Critical rate is calculated at all depths and the reported rates are maximum rates calculated (at variable depths) throughout well history.
5. Specified - Using this option, you can manually specify the fixed depth at which critical rates are to be computed throughout well history.
6. Multiconfig - To compute the critical rate at different depths, specific to each wellbore configuration, across well history.

You can toggle pressures on and off (using the 'Show pressures' button to the top-right of the liquid loading plot) to view the currently used bottomhole pressure, casing and tubing pressures and the difference between them on the same plot.

3.4.4 Critical rate correlations in nodal analysis

Here's an example well use case justifying the use of 'End of tubing' as the critical rate depth and quantifying the gas rates needed to prevent liquid loading using the Turner correlation:

In terms of critical velocities

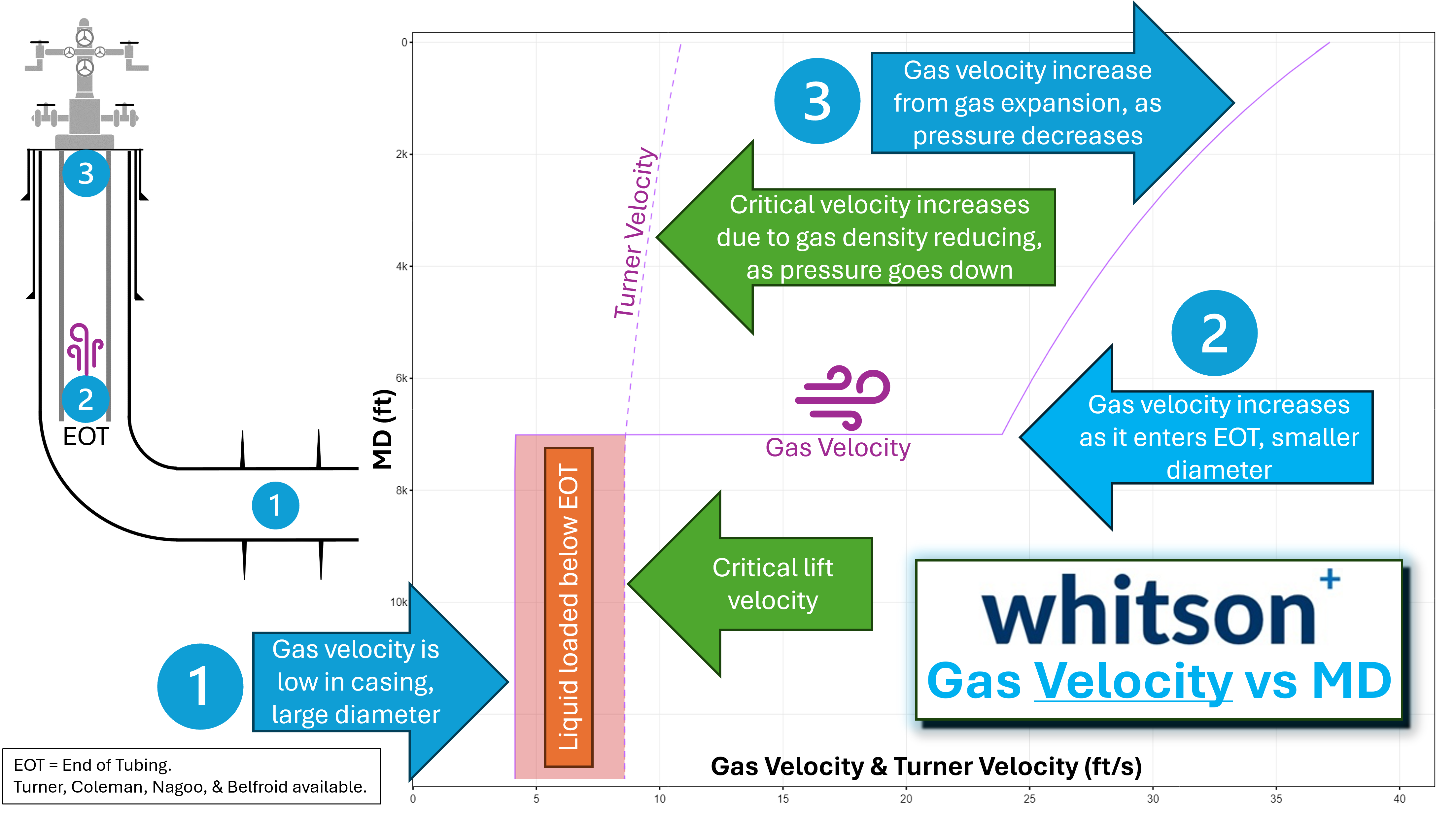
In terms of critical rates

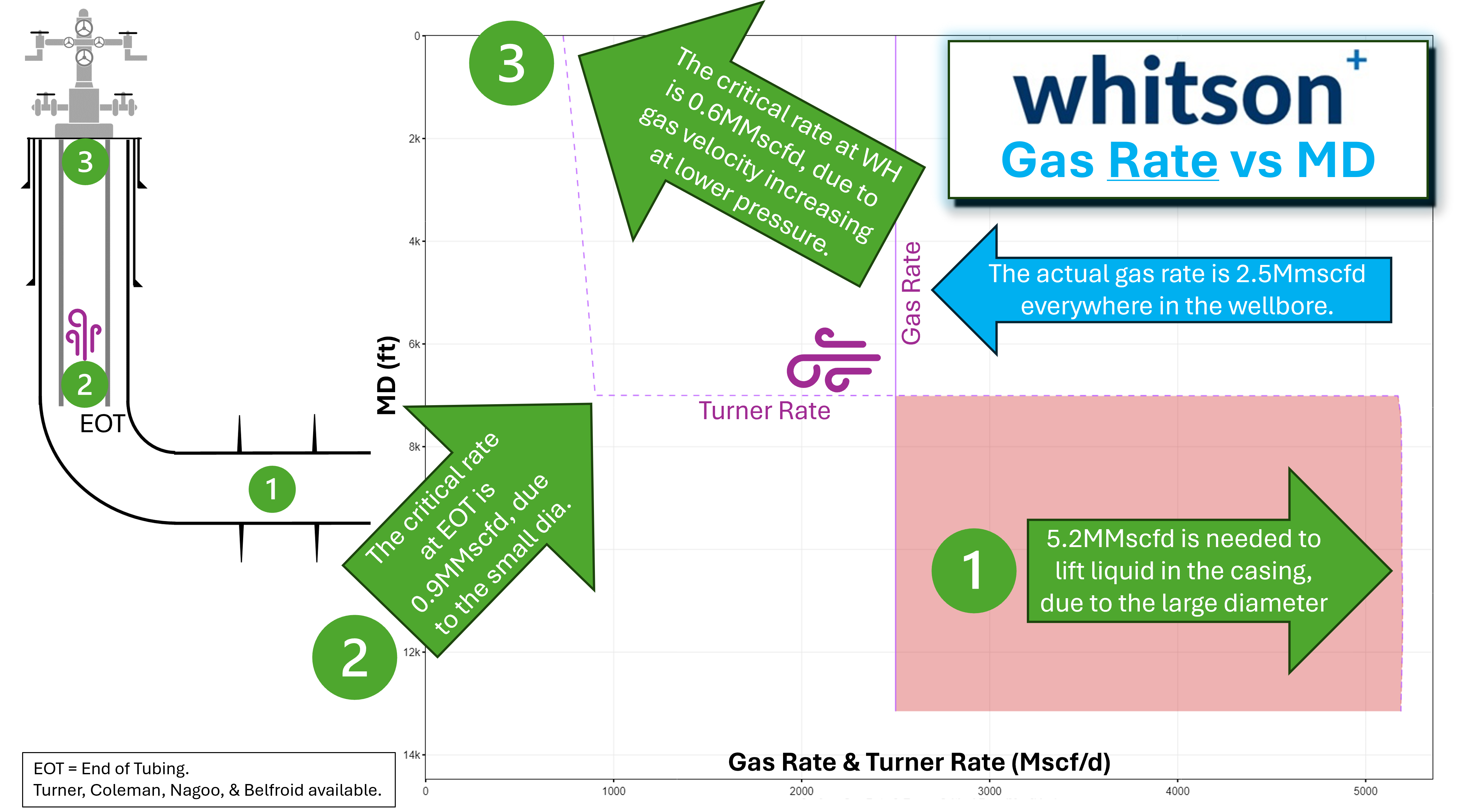
You can compute the critical and superficial velocity/rate vs depth and generate these plots in the Gradient tab of the Nodal Analysis feature for your wellbore.

3.4.5 Indentifying Liquid Loading - Some practical tips

Two typical signatures of a well experiencing liquid loading are

1. the gas rate drops without a change in the wellhead (casinghead and/or tubinghead) pressures.
2. the casing-tubing goes from flat to increasing (casing pressure minus tubing pressure is pretty flat when unloaded, once loaded, the tubing pressure starts to fall, so the delta between casing and tubing goes from flat to increasing)

3.5 Correlation Tuning

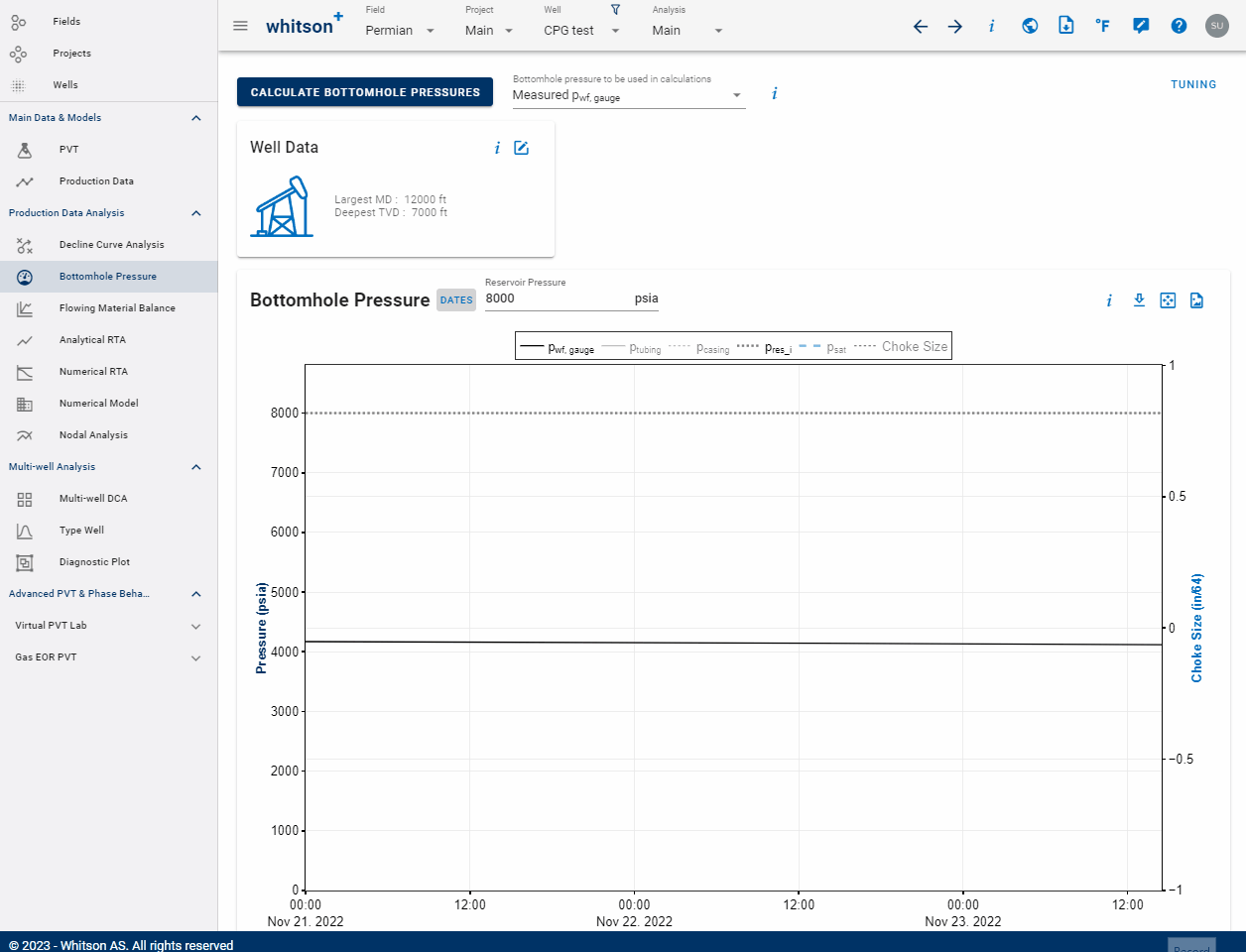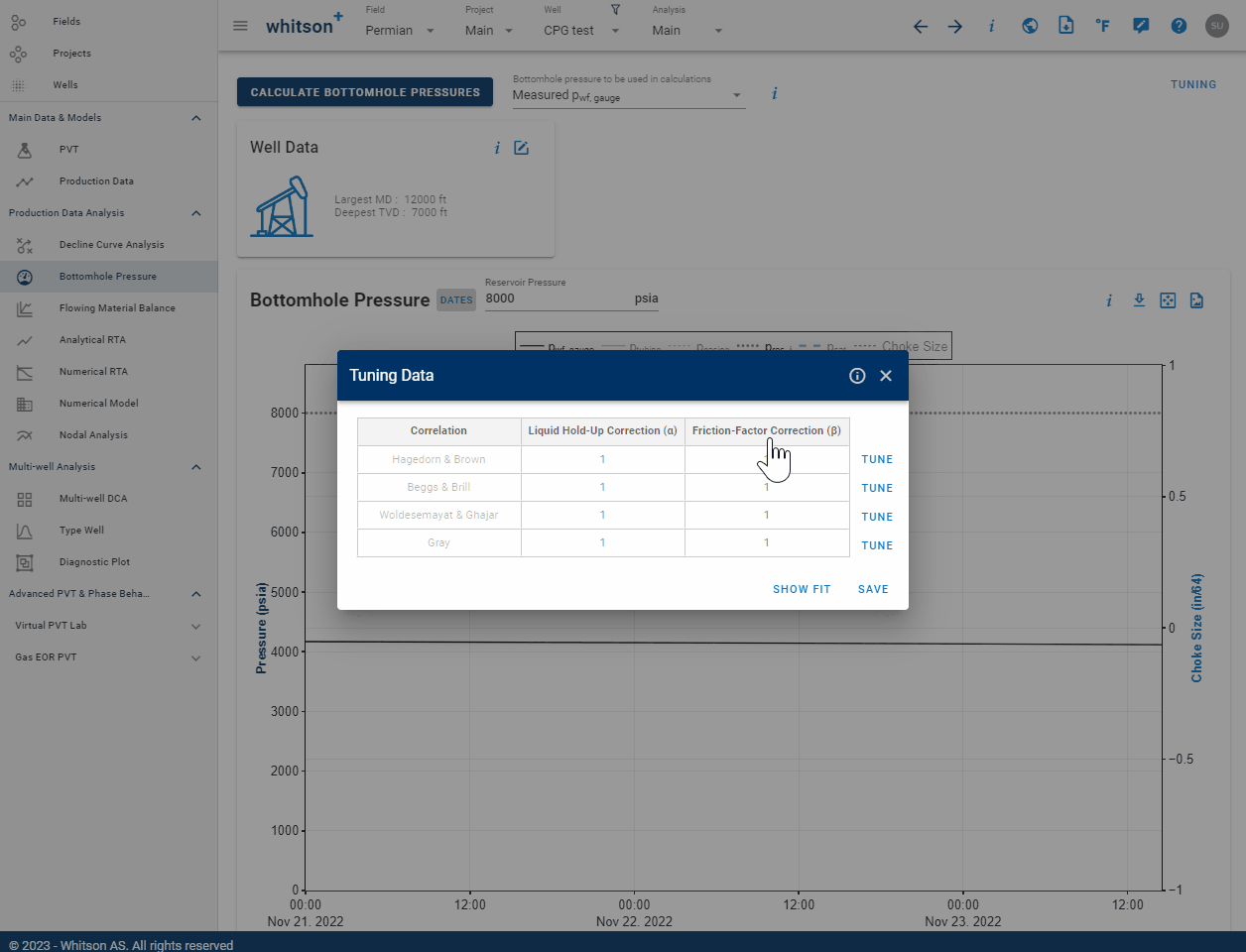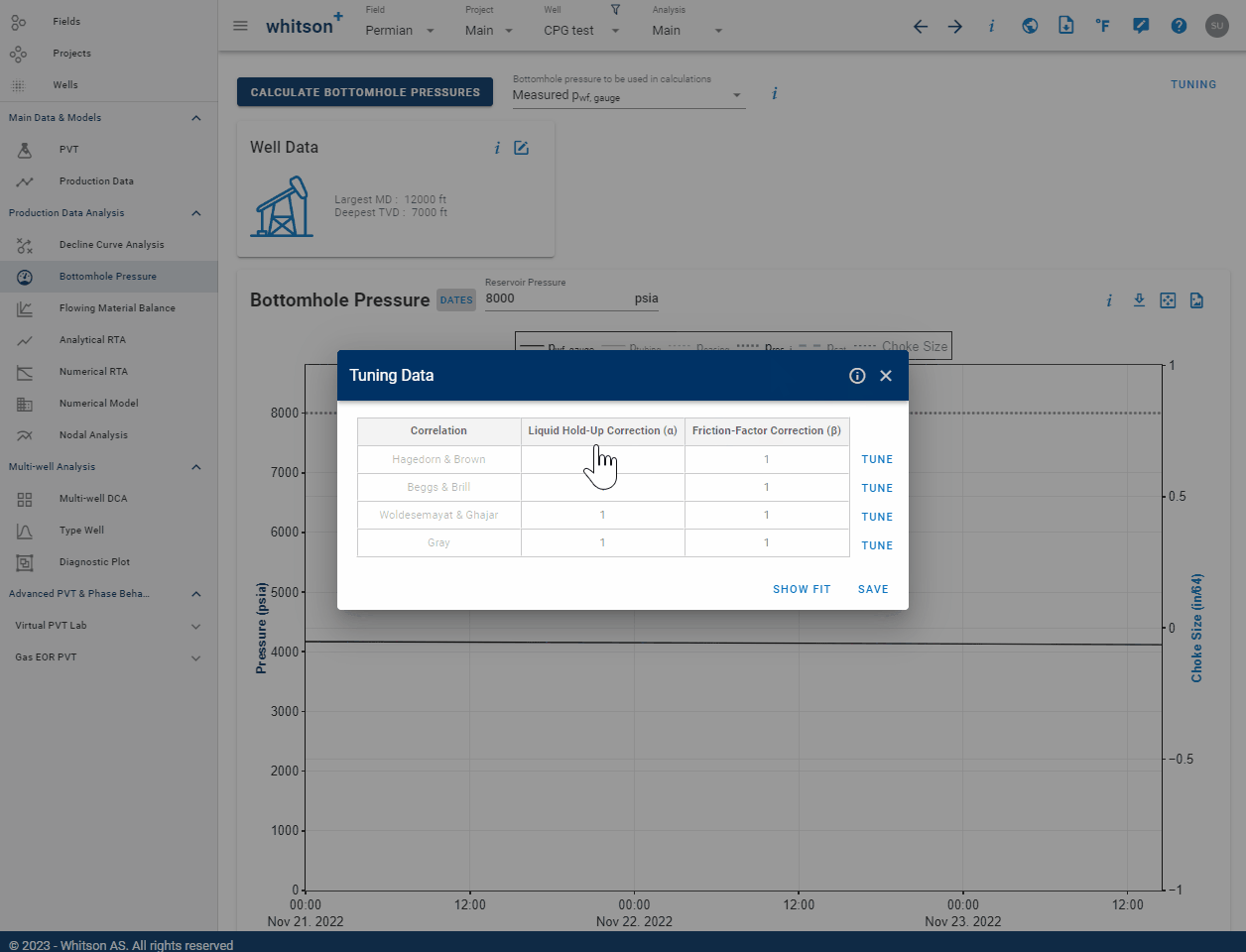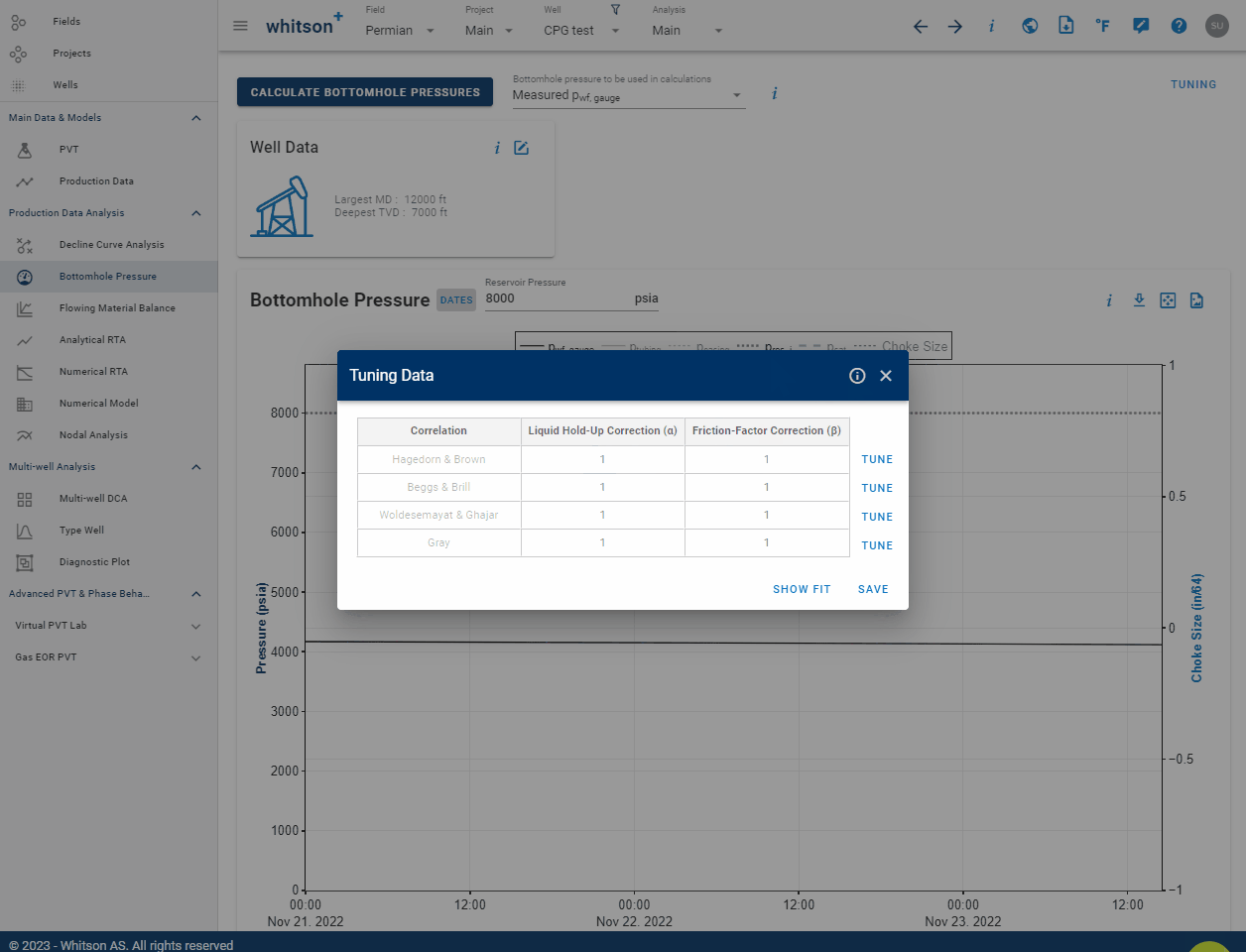
The BHP tuning functionality can be accessed by clicking Tuning to the upper right of the BHP feature as seen below.

The following video illustrates a practical example of "BHP correlation tuning to measure gauge data"

3.5.1 Correcting the Properties

The multiphase-flow correlations used to compute the bottomhole pressure can be tuned in whitson+. This is achieved by correcting the liquid hold-up by a parameter \(\alpha\), and the friction factor by a parameter \(\beta\). Correcting the liquid hold-up affects mainly the gravity pressure drop, while correcting the friction factor affects the friction pressure drop. The corrections are made as follows:

Liquid Hold-Up Correction:

The liquid hold-up, \(H_L\), is always lower bounded by the liquid flux fraction, \(C_L\), and upper bounded by 1. To honor this bracketing in a tuning process, it is easier to convert the liquid hold-up into an equivalent slip velocity that is only lower bounded by 0, and then apply the \(\alpha\) parameter as a correction multiplier. The slip velocity is defined as

$$\begin{equation} v_s = v_g - v_L = \frac{v_{sg}}{1-H_L}-\frac{v_{sL}}{H_L} \label{eq:slipVelocity} \end{equation}$$

where \(v_g\) and \(v_L\) are the gas and liquid velocities, and \(v_{sg}\) and \(v_{sL}\) are the superficial gas and liquid velocities. Solving (\ref{eq:slipVelocity}) for \(H_L\), we get:

$$\begin{equation} H_L=\frac{-(v_m-v_s)\sqrt{(v_m-v_s)^2+4v_sv_{sL}}}{2v_s} \label{eq:liquidHoldUp} \end{equation}$$

The liquid hold-up correction is made by

1. Compute the slip velocity \(v_s\) from \(H_L\) predicted by the default/untuned correlation using Eq. (\ref{eq:slipVelocity})
2. Multiply the slip velocity by \(\alpha\) to get \(v_{s}^{corr}=v_s\alpha\)
3. Calculate \(H_L^{corr}\) with the corrected slip velocity \(v_s^{corr}\) using Eq. (\ref{eq:liquidHoldUp})

Friction-Factor Correction:

The friction factor is corrected by multiplying the calculated friction factor from the default/untuned correlation by \(\beta\).

3.5.2 Selecting the Measured Pressure Points to Tune

The tuning procedure includes a routine that selects a subset of the measured gauge data over time. This is done for two reasons, (1) to speed up the tuning process by computing less pressures points, and (2) to minimize the effect of outliers. The sampling procedure involves three steps:

1. Remove outliers that has more than a 20% relative difference from its neighbors.
2. Compute a moving average of the filtered data
3. Sample the moving average at a constant spacing of 20 days.

3.5.3 Correlation Tuning Using Measured Pressures from an ESP

Measured pressures from an electric submersible pump (ESP) should not be used to tune the bottomhole-pressure correlations. The reason for this is that the computed pressures from wellhead to gauge (situated at the ESP inlet) does not account for the delta-pressure caused by the ESP.

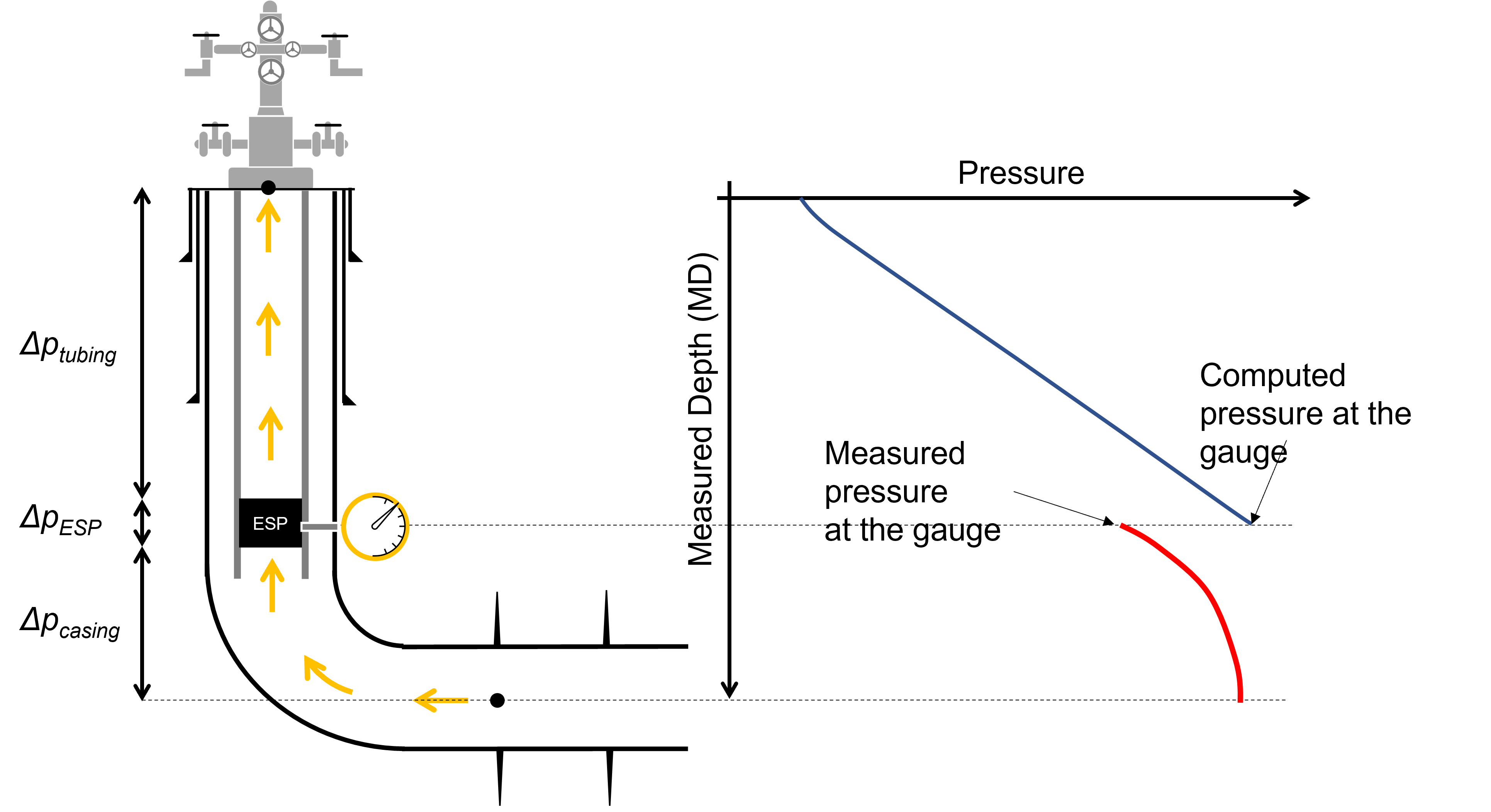
3.6 Estimating Initial Reservoir Pressure in whitson⁺

Here we are estimating reservoir pressure from flowing pressure and rate data, typically acquired for most wells. These are just approximation methods involving uncertainty and other tests, specific to this purpose, like Diagnostic Fracture Injection Tests (DFIT), downhole formation testing tools, pre-frac step-rate injection tests, post-frac instantaneous shut-in pressure combined with frac gradient relationships, opening pressure of the first port for packer/sleeve completions, etc., should be used wherever available.

In whitson⁺, the already available rates and pressure data can be used in two ways to estimate reservoir pressure:

3.6.1 Reservoir Pressure from flattening of flowback BHP before hydrocarbon production

This technique is outlined in Jones et al[5], (URTeC: 1934785), and consists of three steps to diagnose reservoir pressure from flowback data (preferably hourly):

1. Calculate BHP for the flowback data using a suitable multiphase flow correlation.
2. Plot BHP along with rate and other pressure data.
3. Look for a flattening or minimum BHP, just before the first measurable hydrocarbon production is reported. Casing pressure might show a similar pattern too. This flat portion or minimum in the BHP curve is the estimated reservoir pressure.

Assumptions

Produced fluids during flowback are initially 100% water, with delayed hydrocarbon breakthrough. Flowback begins shortly after the frac was completed and the frac plugs are drilled out.

This is so that there is least uncertainty in the calculated BHP initially and the BHP at the beginning of flowback is higher than the estimated reservoir pressure, so the "frac charge" is not allowed to dissipate through leakoff (such as during an extended shut in or installation of artificial lift after the frac job). Hourly flowback data makes it easy to identify the pressure behavior associated with first hydrocarbon production.

The simplest explanation for this might be that trace amounts of immeasurable hydrocarbons (due to relatively high water rate) start entering the wellbore and arrest the decline in wellhead pressure, hence BHP tends to remain flat just before measurable hydrocarbon is separated from the flowback frac water and rates are reported.

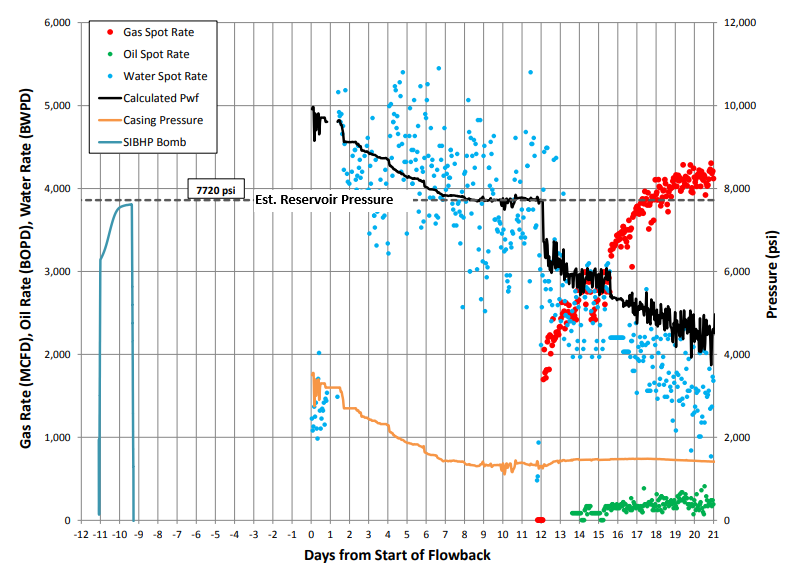
Example flowback data for estimation of reservoir pressure (from Jones et al, URTeC 1934785)

The flattening of BHP, identified as reservoir pressure, may be too short or completely missing if the drawdown is too aggressive, productivity is too low, finite conductivity fractures, near wellbore skin damange, or large changes in choke instead of gradually and monotonically opening them. In these cases, the data has step changes in rates and pressures, or BHP reduces quickly and significantly below the actual reservoir pressure - making it really difficult to identify reservoir pressure.

In the BHP feature, you can plot rates and pressures simultaneously, as outlined above by clicking the 'Show rates, surface pressures' button on the top right of the BHP plot.

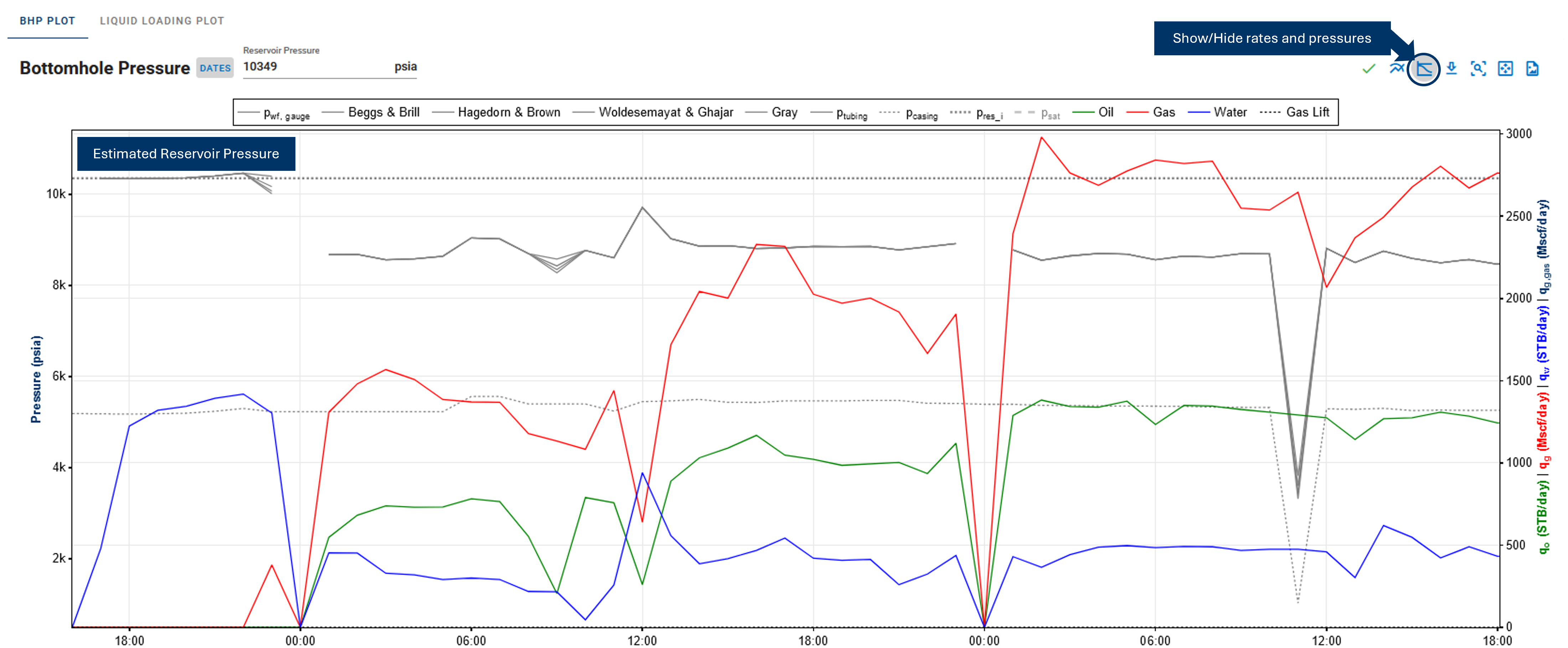
Be sure to zoom into the very early time section of the data and appropriately adjust pressure and rate axis limits on the plot to display a diagnostic plot similar to the one referenced from the paper.

3.6.2 Reservoir pressure from IPR

Here are the steps to estimate reservoir pressure from an approximate IPR fit to BHP vs Rate data:

1. Calculate BHP for the pressure and rate data available.
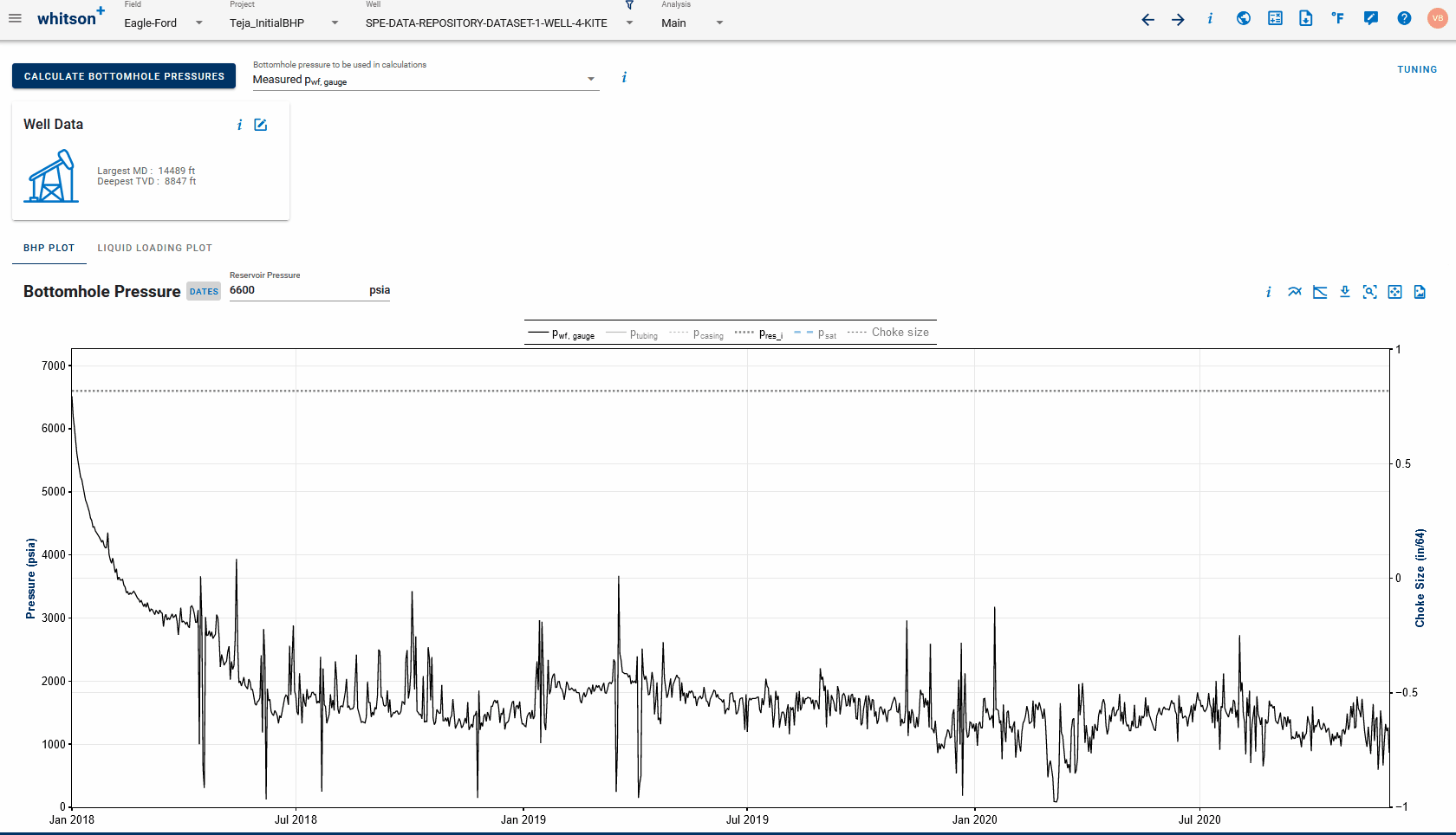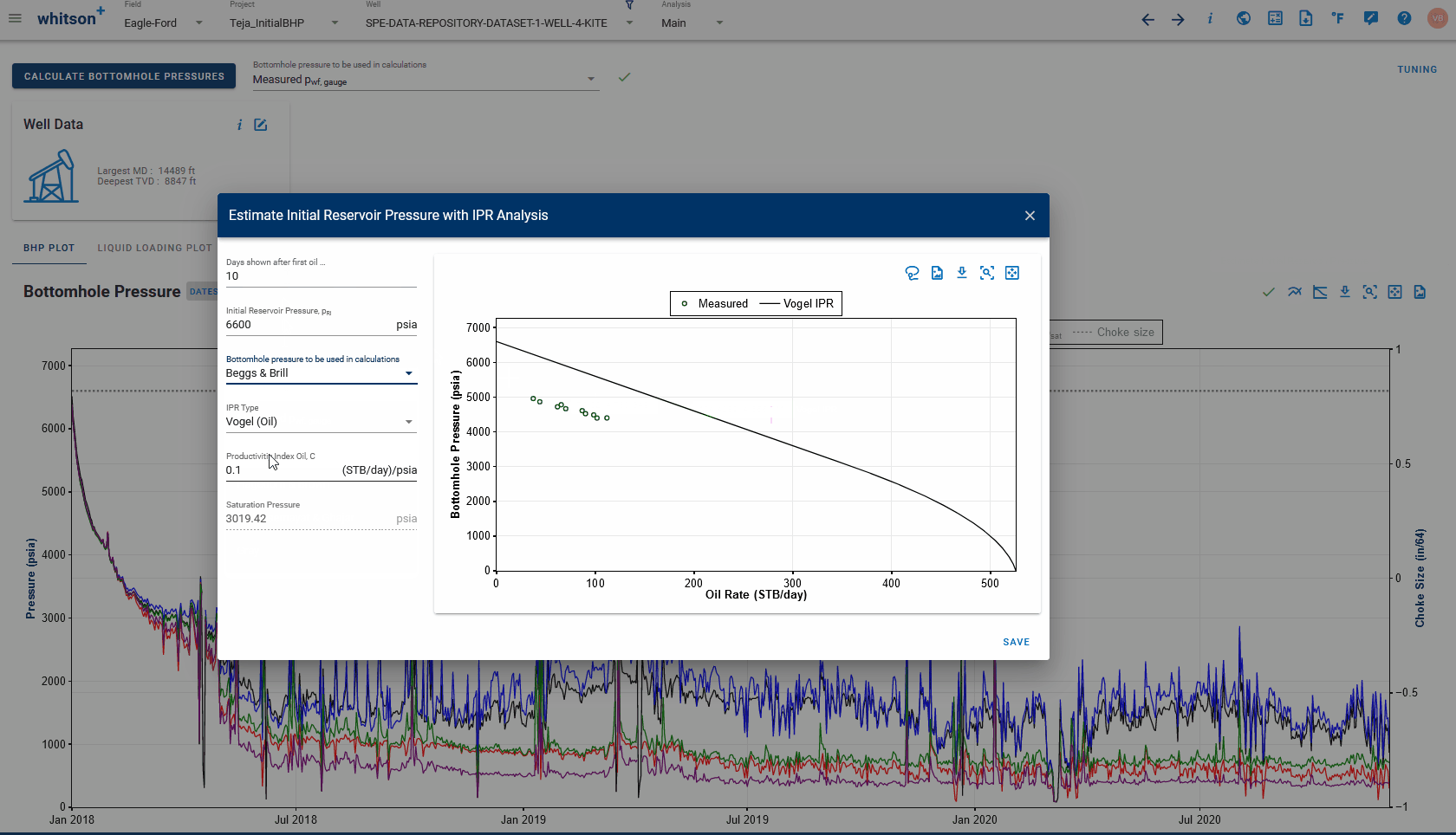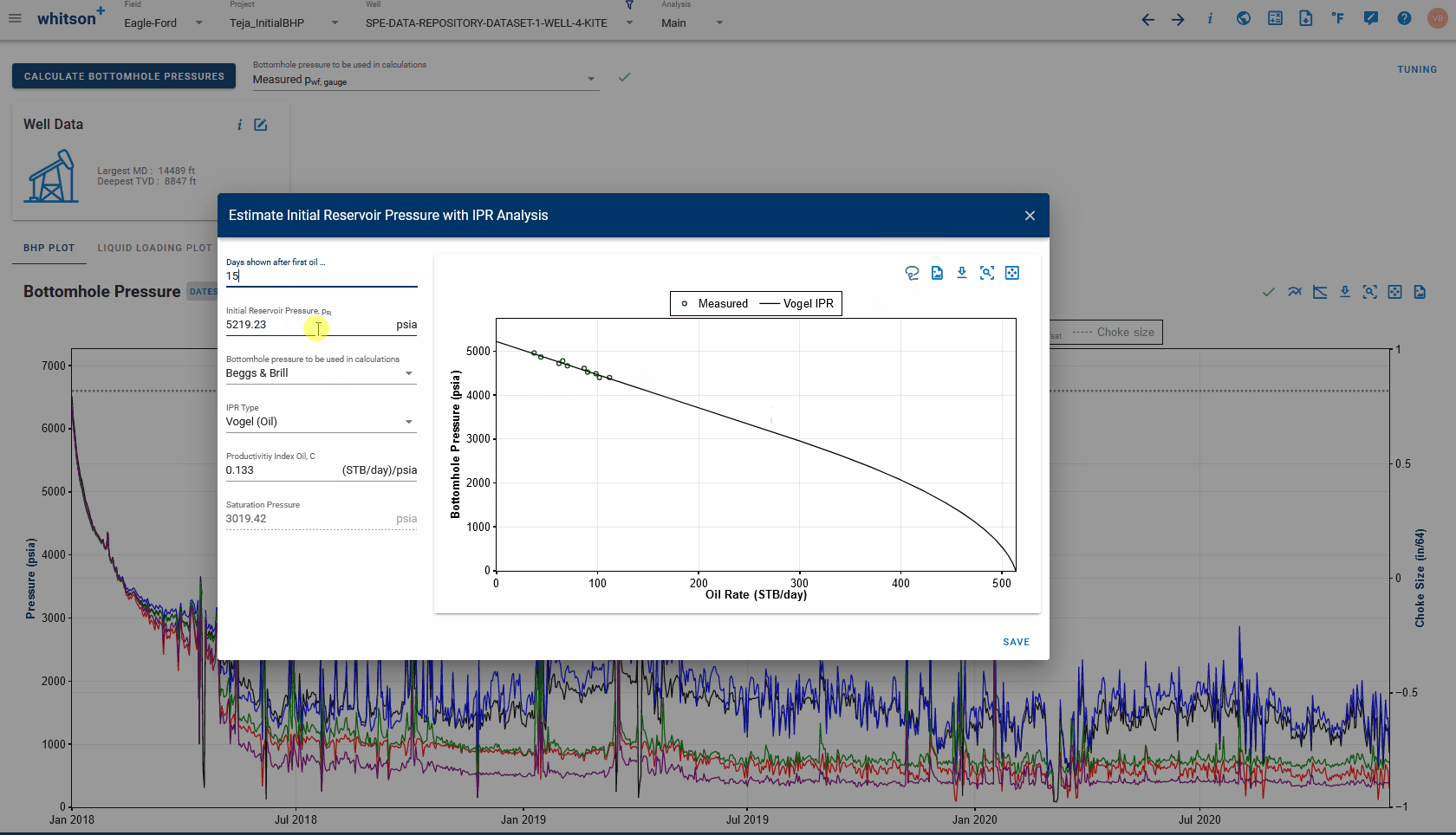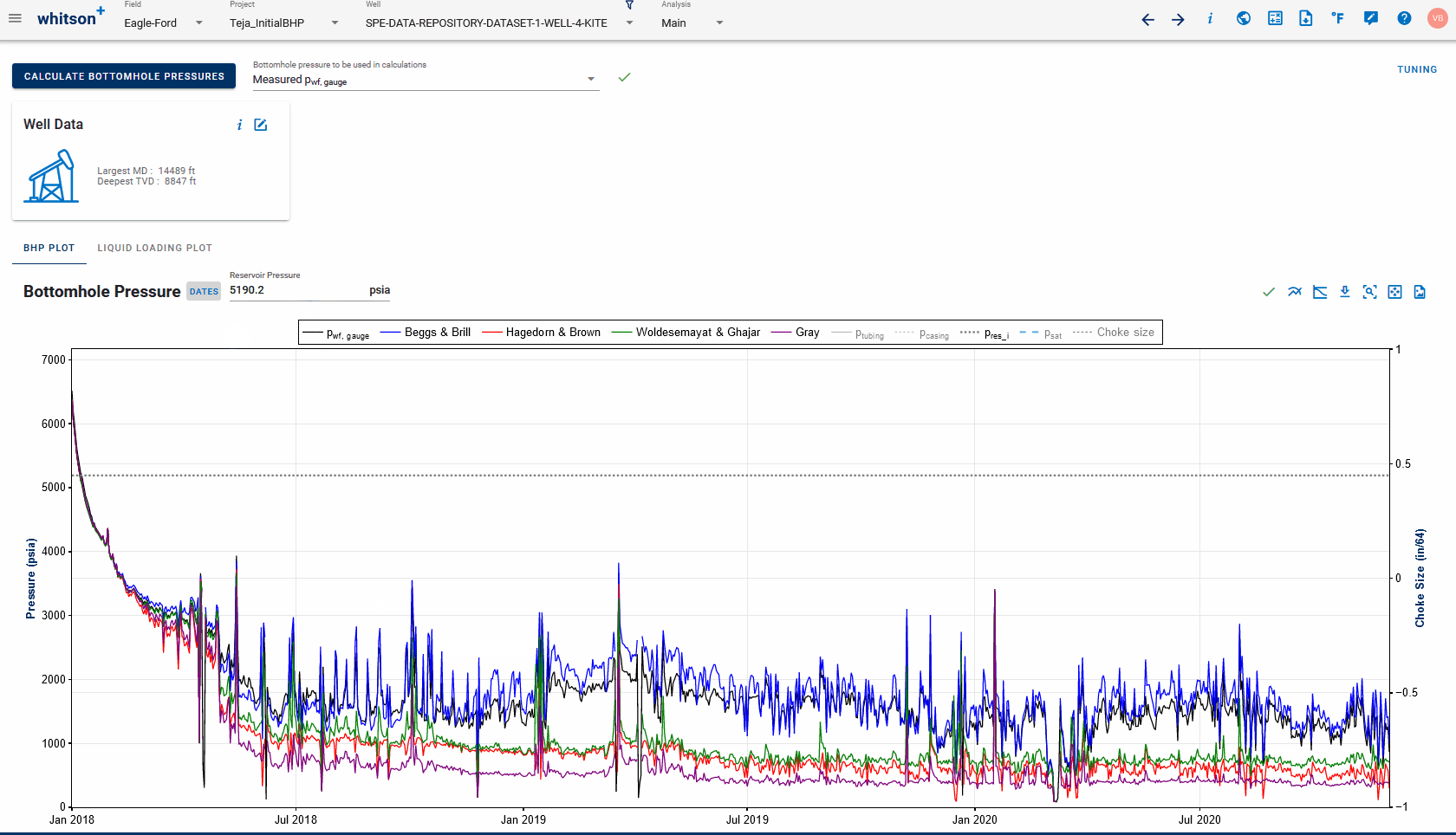
2. On the Bottomhole Pressure plot, click 'Estimate Initial Reservoir Pressure' button on the top-right. This opens a new dialog box allowing you to view BHP vs rate plots to choose the IPR type, the BHP correlation to be used and number of days of data to be displayed on this plot.
3. By default, the oil wells will plot the calculated BHP vs. measured oil rate data for the first 10 days after oil breakthrough, and use the Vogel's IPR curve. Alternatively, for gas wells, the plot defaults to BHP vs gas rate and C&n or the backpressure equation for IPR type.
4. Lasso fit at least 2 or more points to calculate the slope or productivity index and the saturation pressure (from the well's PVT) is used to set up an approximate IPR fit to the data.
5. Extrapolation of this IPR to the y axis (or the intercept) gives the initial reservoir pressure.
6. Click save to update the initial reservoir pressure for the well with this value.

These steps are shown in the GIF below:

3.7 Activate BHP Injection Mode

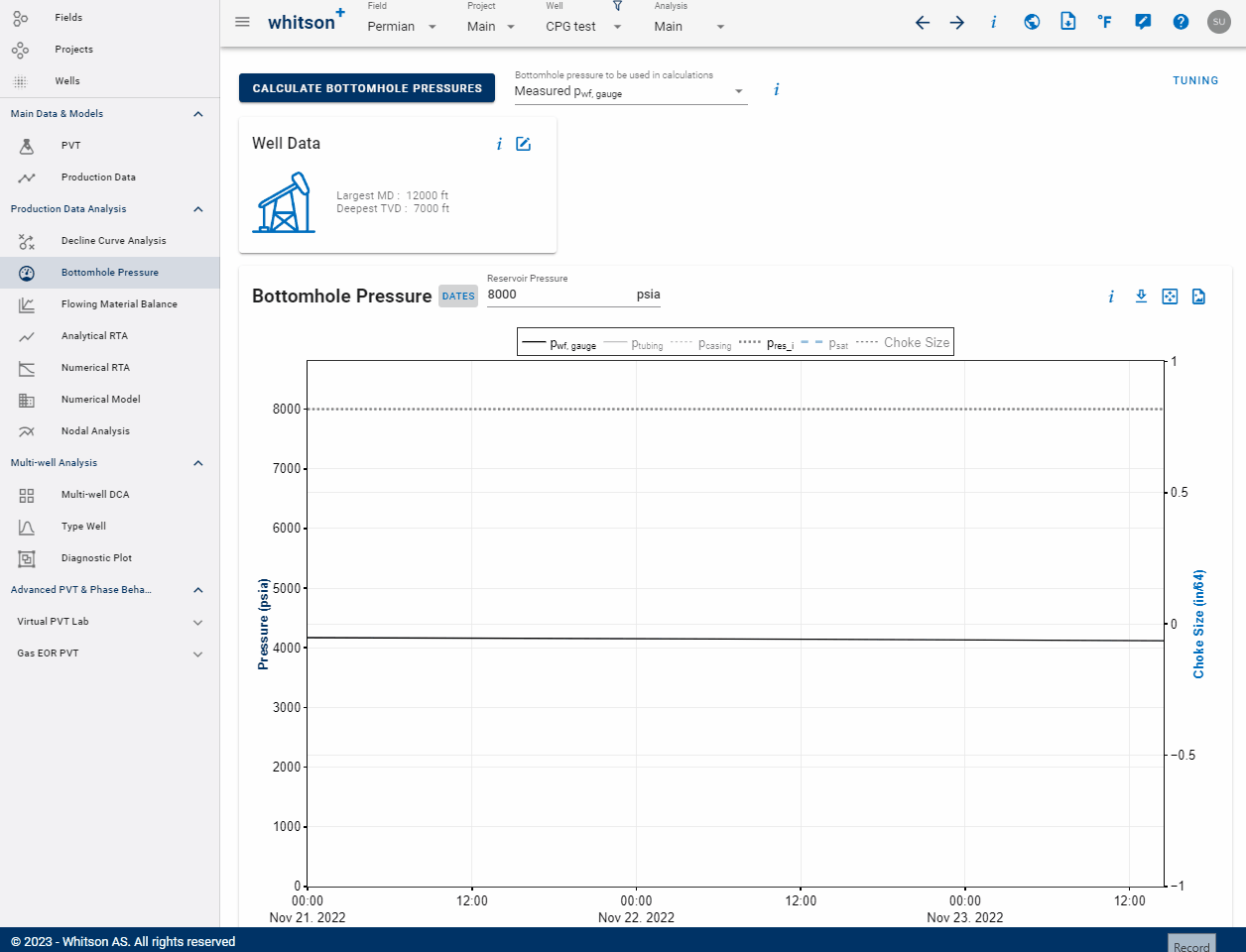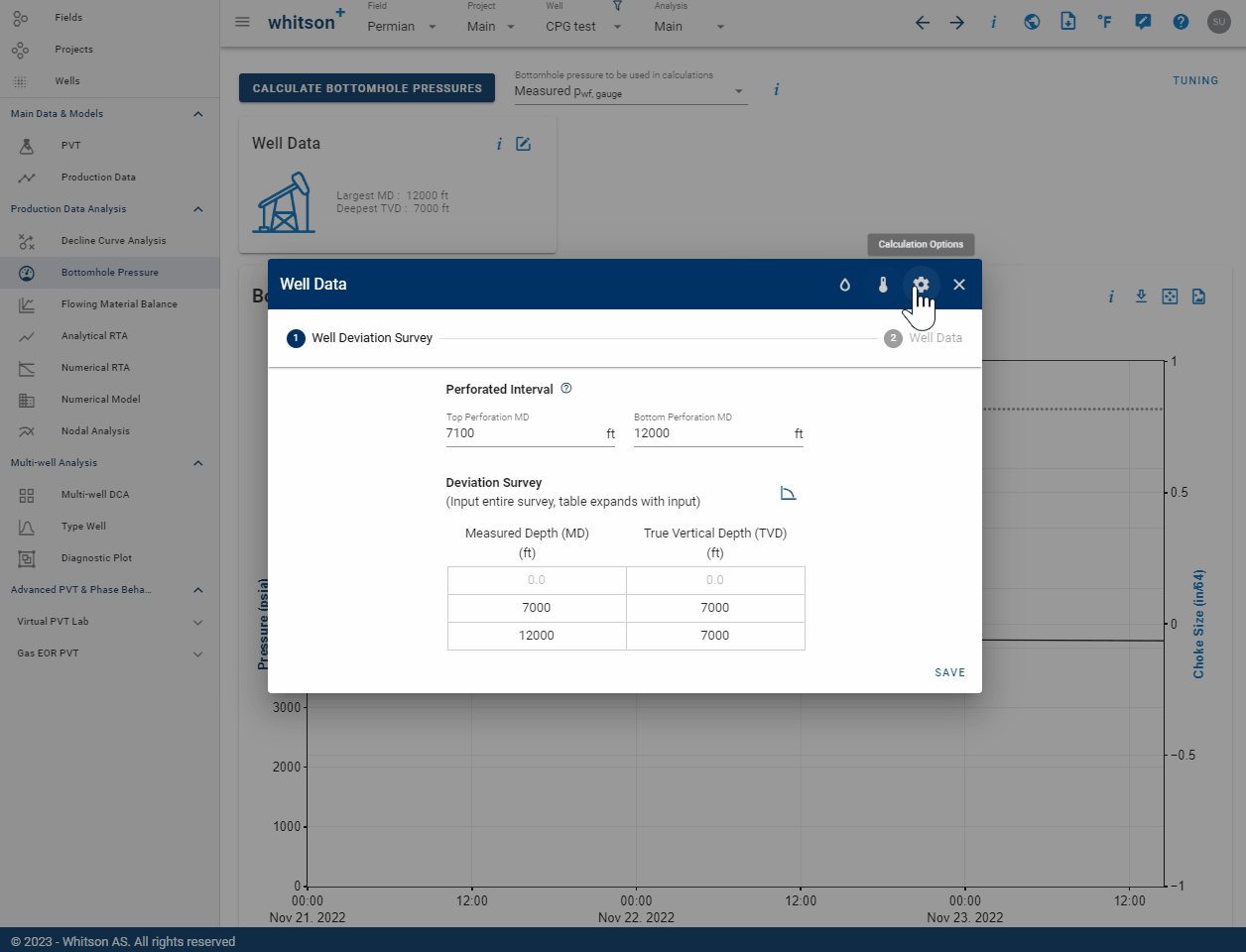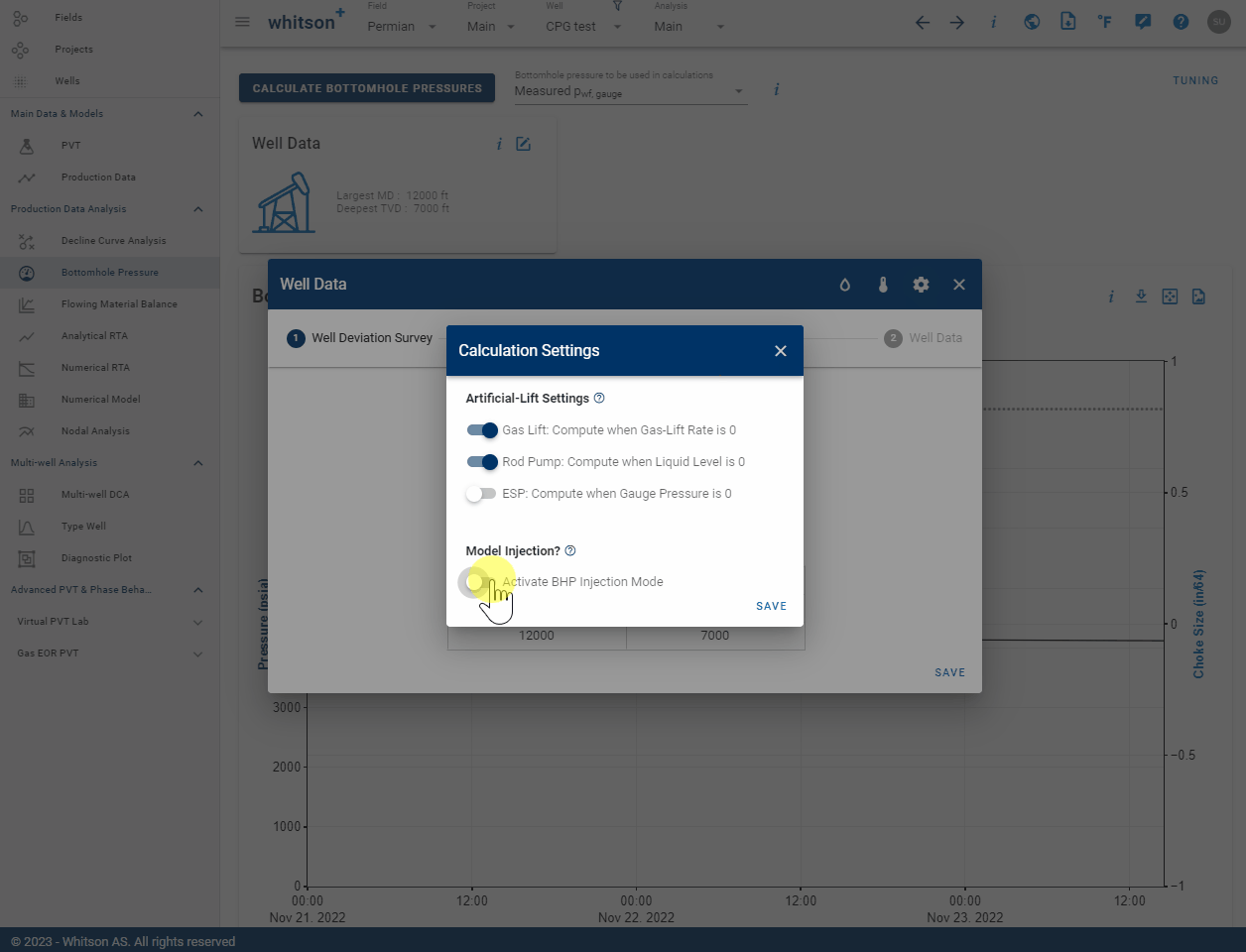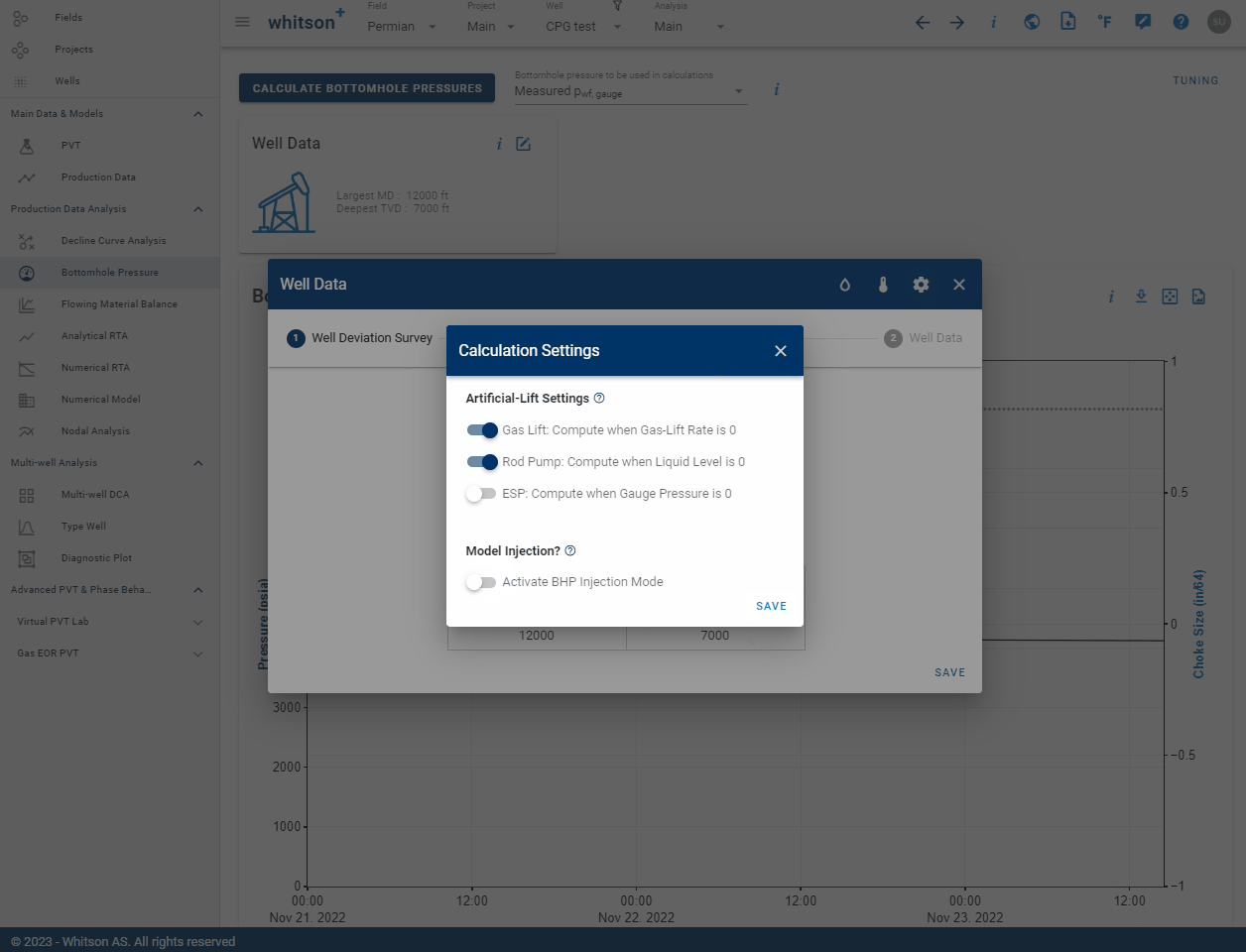
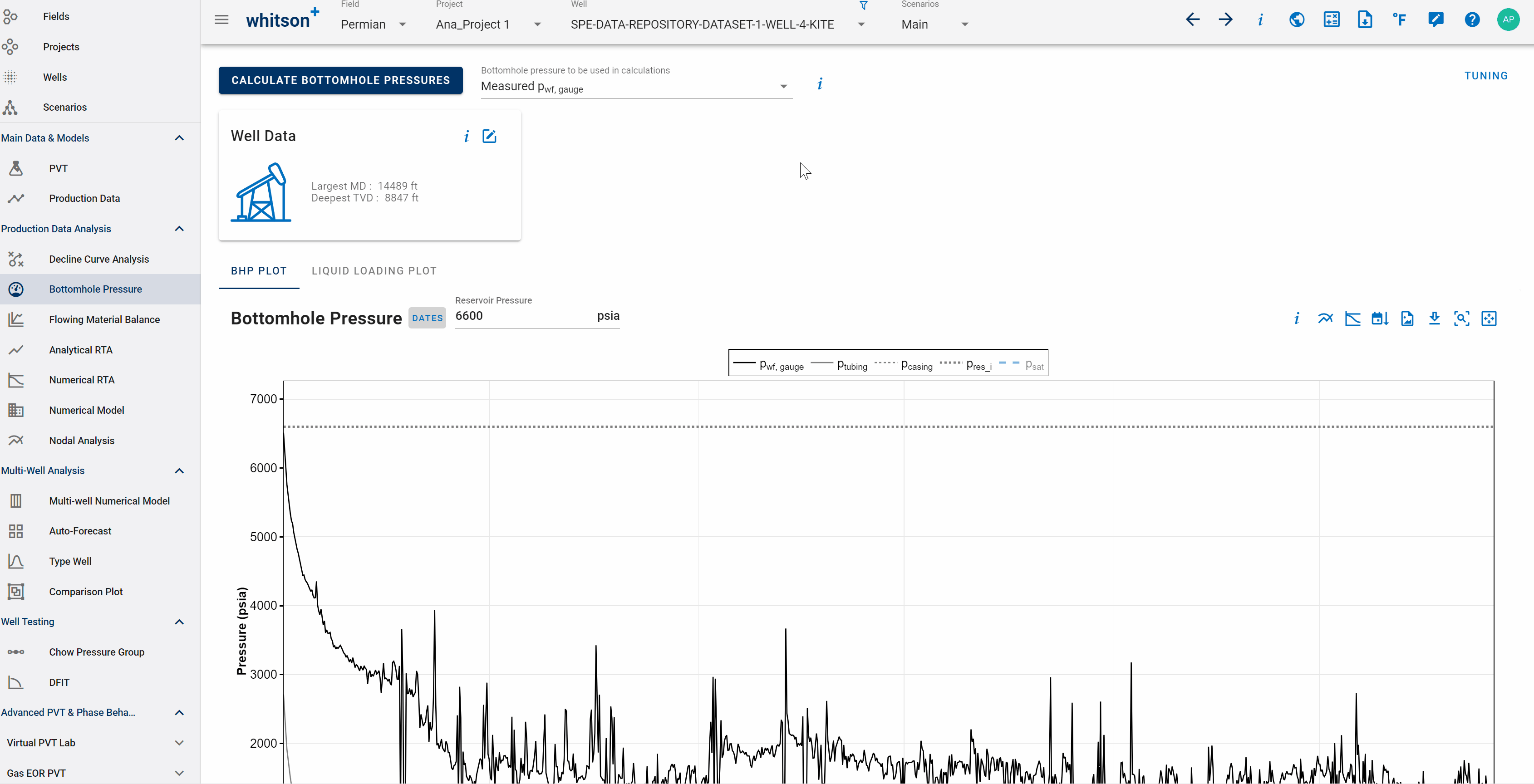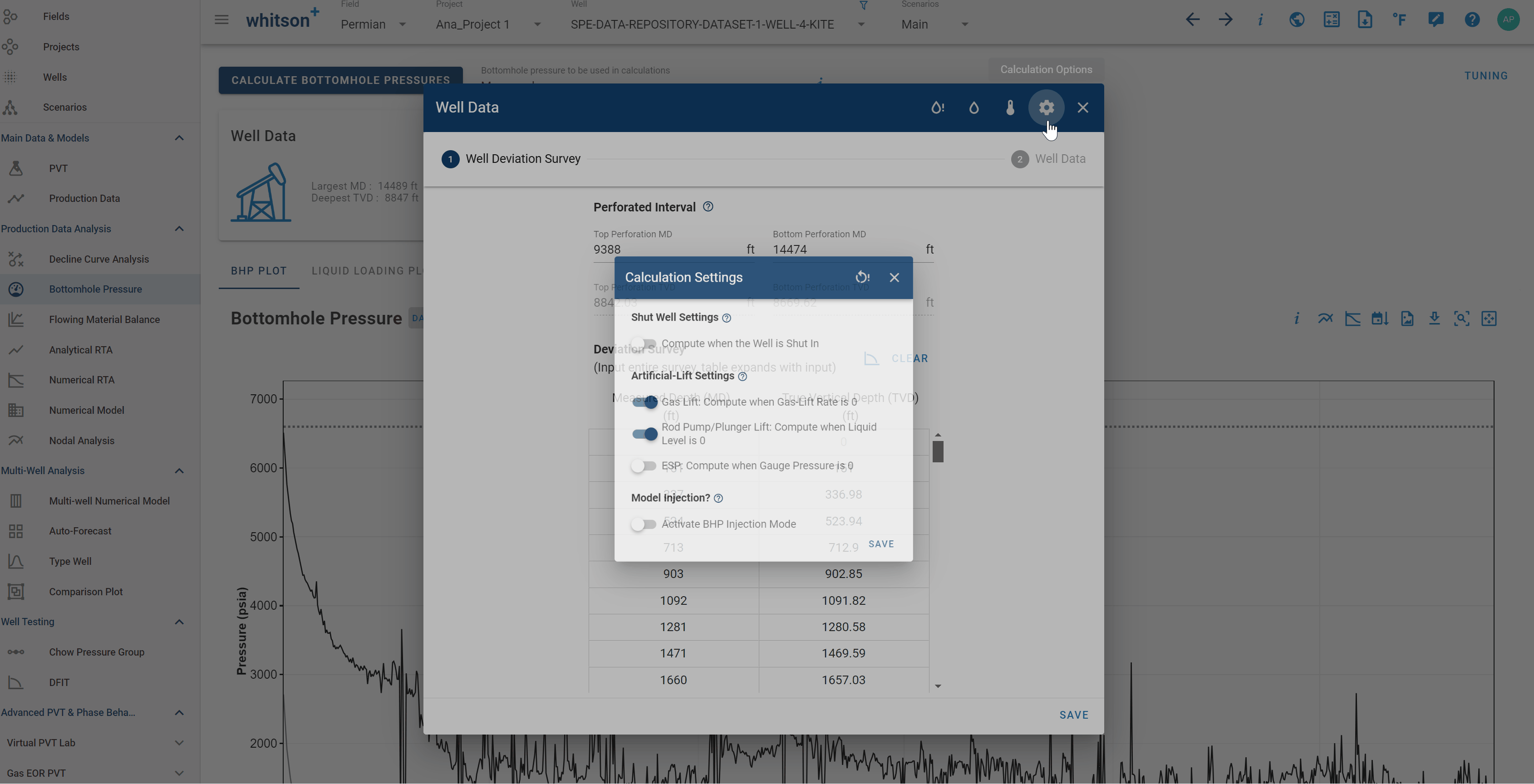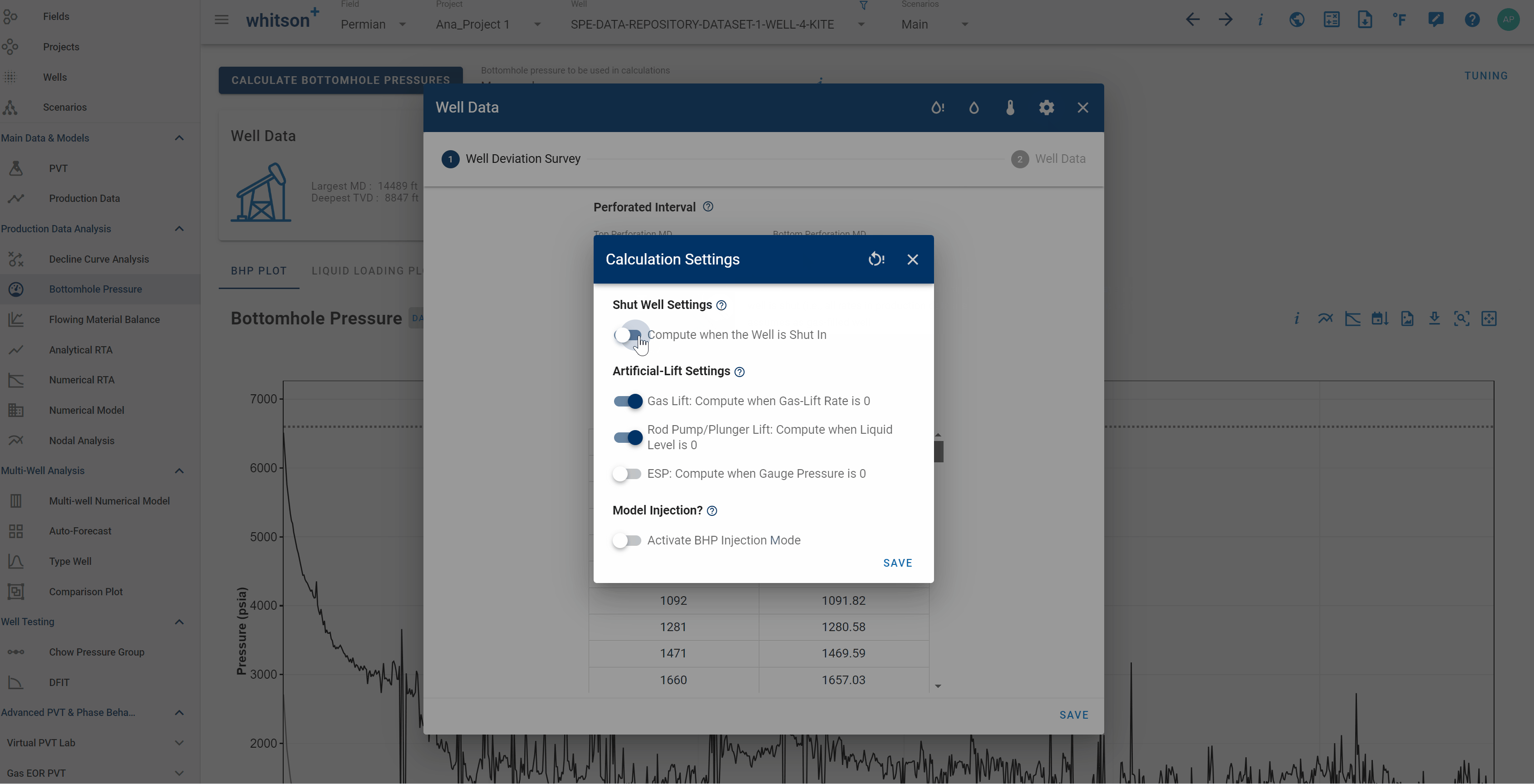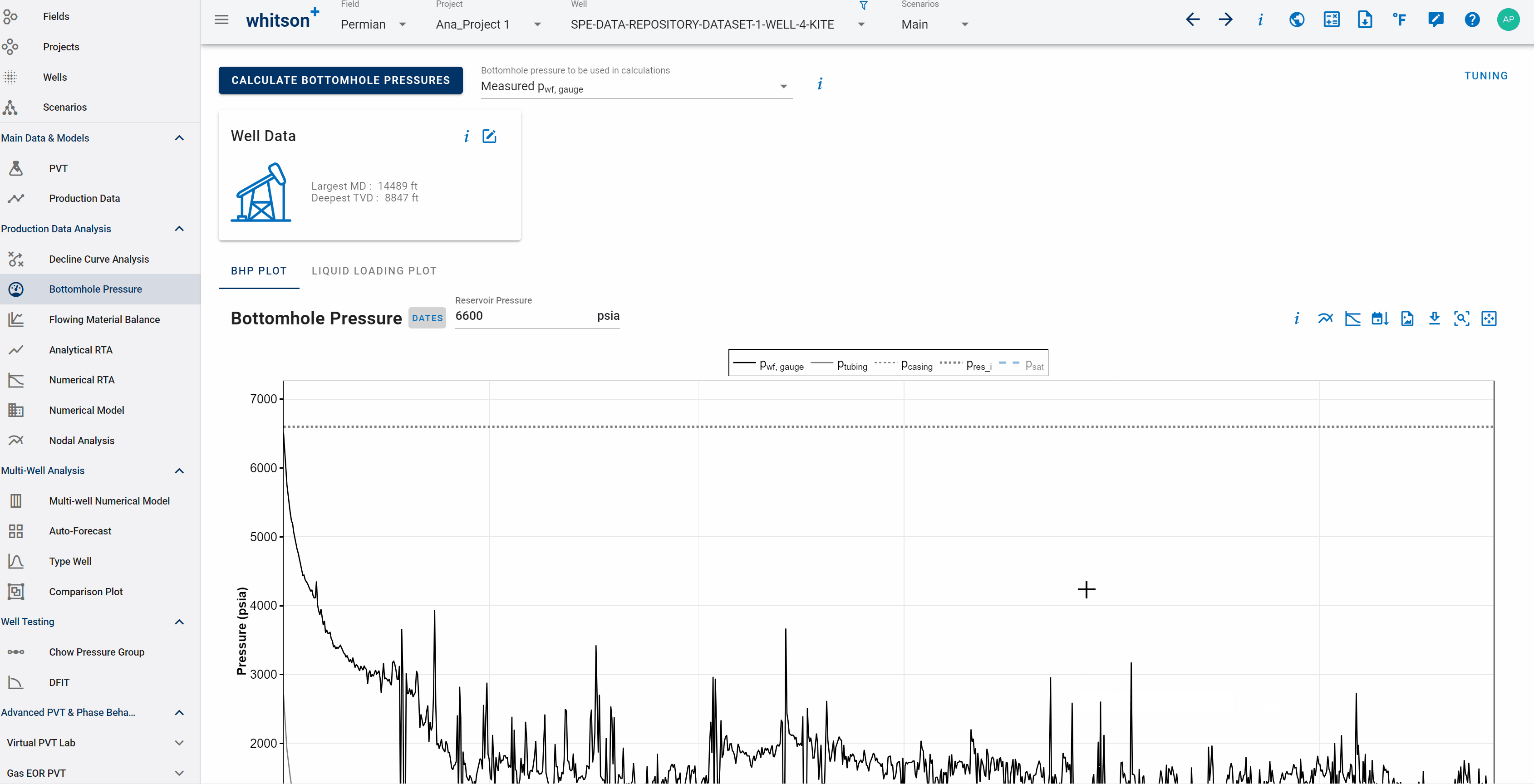
If you want to model the bottomhole pressure during an injection process, that can be done by activating the BHP injection mode. This is done in the Calculation Settings in the Well Data card as seen above. When enabled, this switch allows to simulate the pressure at the bottom of the wellbore during injection. All uploaded rates (e.g. oil, water or gas) will be assumed to be injected rates.

3.8 Shut Well Settings

Select whether the BHP calculator should skip or compute the BHP for the days where the well is shut (i.e., all rates in production data are missing/zero).

The shut-well calculation assumes a gas-filled well.

References

[1] R.G. Turner; M.G. Hubbard; A.E. Dukler, Analysis and Prediction of Minimum Flow Rate for the Continuous Removal of Liquids from Gas Wells, SPE-2198-PA

[2] Steve B. Coleman; Hartley B. Clay; David G. McCurdy; Lee H. Norris, III, A New Look at Predicting Gas-Well Load-Up, SPE-20280-PA

[3] S. P. C. Belfroid; W. Schiferli; G. J. N. Alberts; C. A. M. Veeken; E. Biezen, Prediction Onset and Dynamic Behaviour of Liquid Loading Gas Wells, SPE-115567-MS

[4] A. S. Nagoo; P. M. Kulkarni; C.. Arnold; M.. Dunham; J.. Sosa; P. O. Oyewole, A Simple Critical Gas Velocity Equation as Direct Functions of Diameter and Inclination for Horizontal Well Liquid Loading Prediction: Theory and Extensive Field Validation, SPE-190921-MS

[5] Jones, R. Steven; Pownall, Brian; Jarrid Franke, "Estimating Reservoir Pressure from Early Flowback Data". Paper presented at Unconventional Resources Technology Conference, Denver, Colorado, USA, 2014. URTeC 1934785.