Nodal Analysis - IPR / VLP

1. Overview

The Nodal Analysis feature provides a simple way of evaluating whether the current well configuration produces the reservoir fluids efficiently, or if a different well configuration would increase the well performance.

1.1 Selection of Production Test Date and Creation of IPR

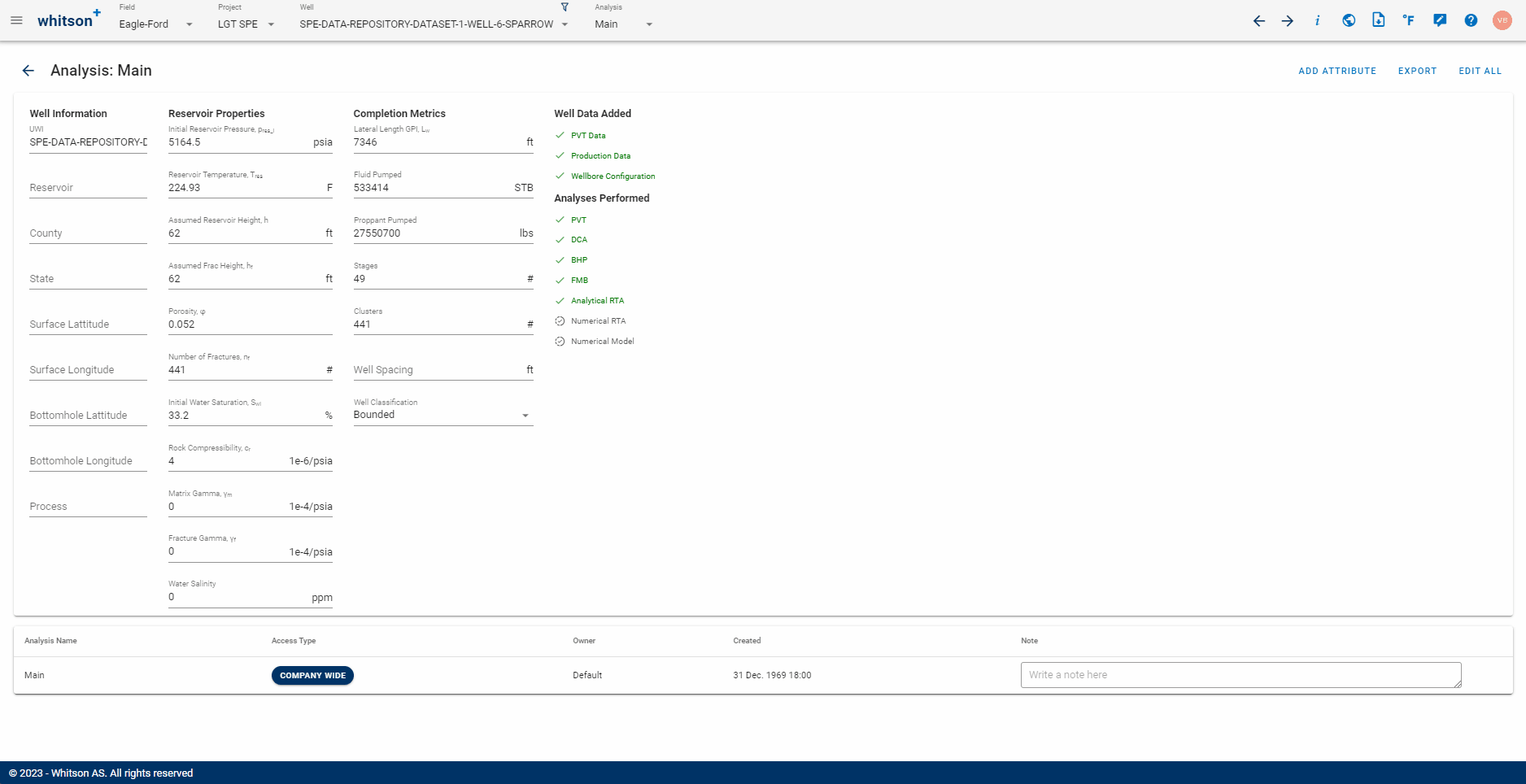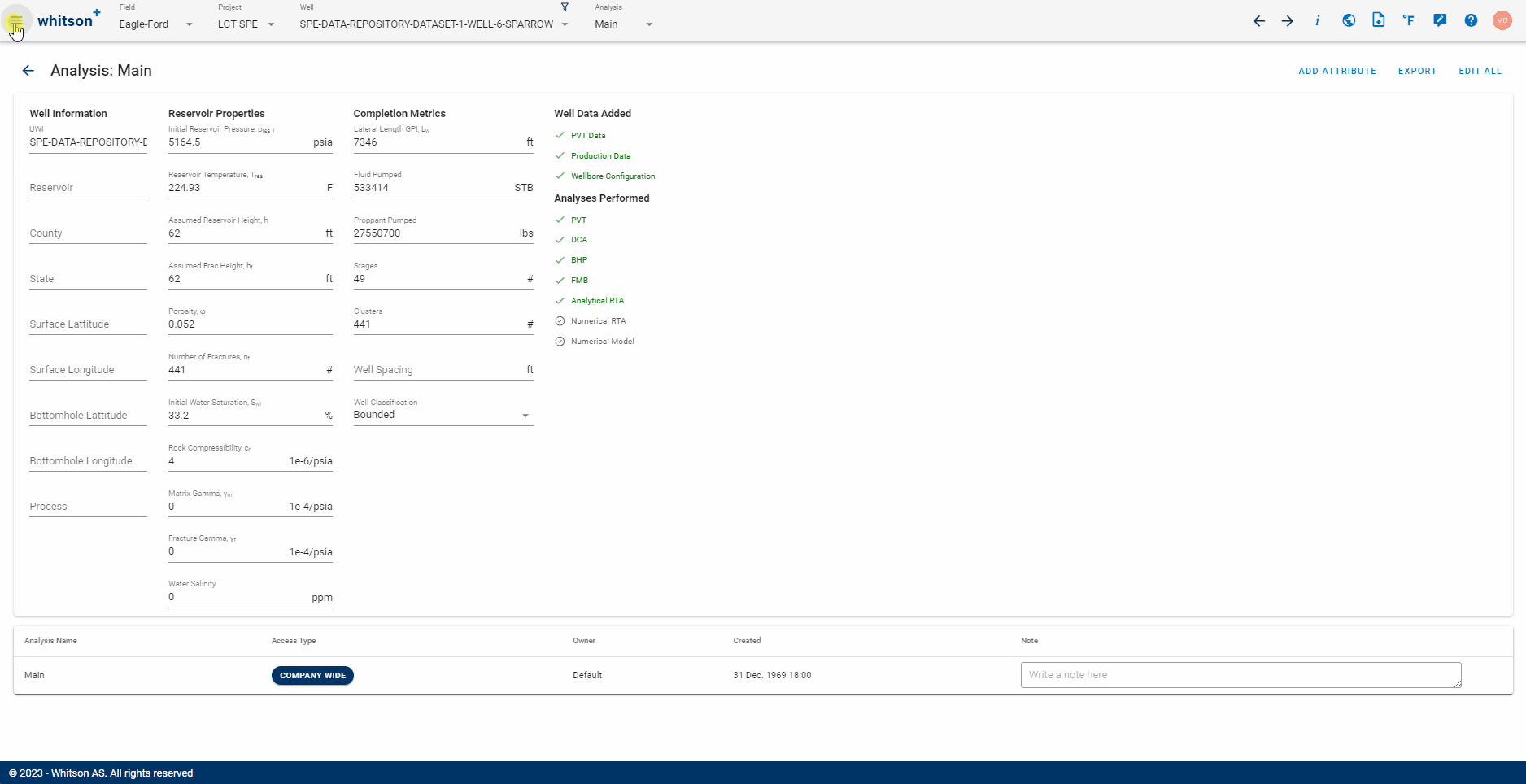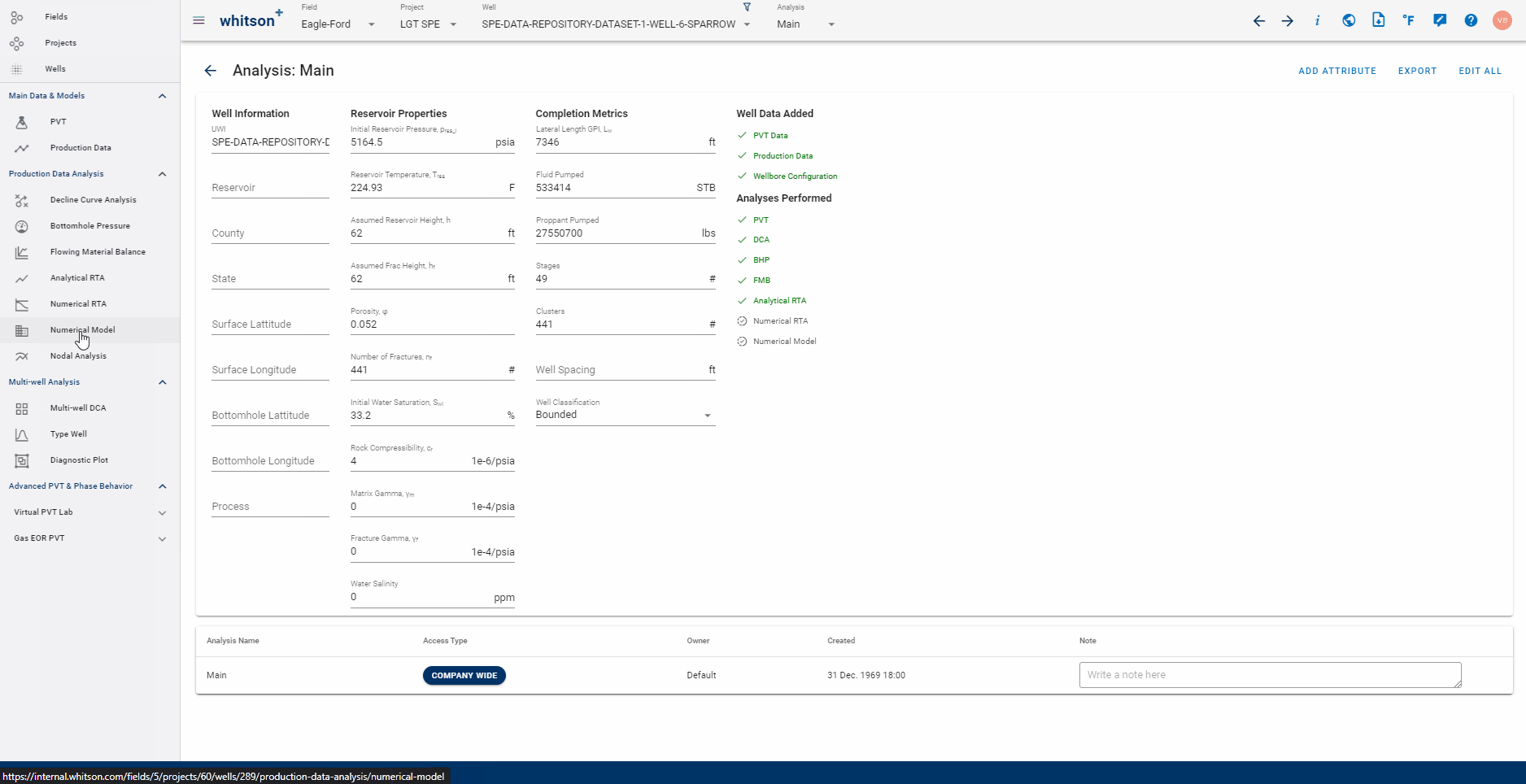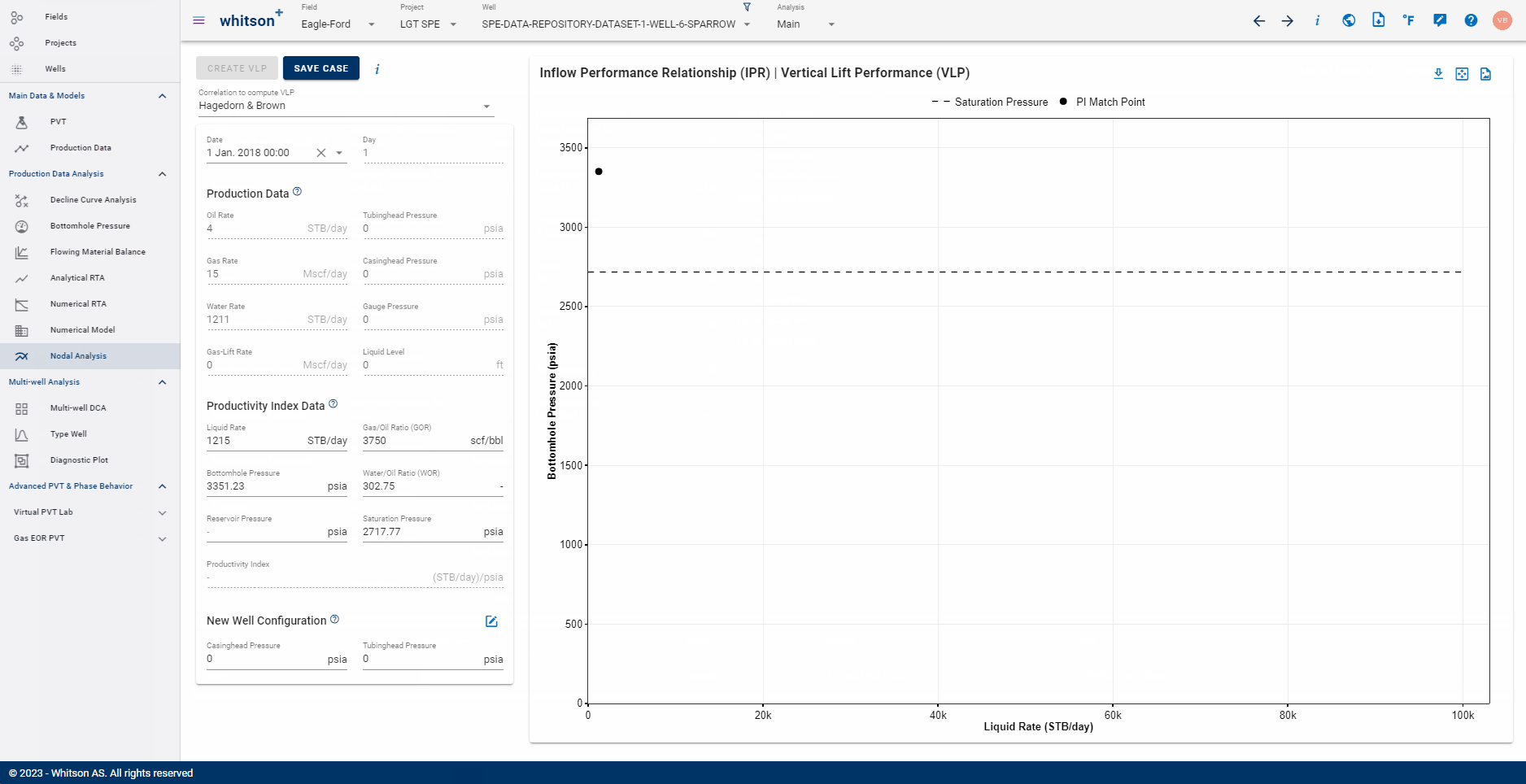
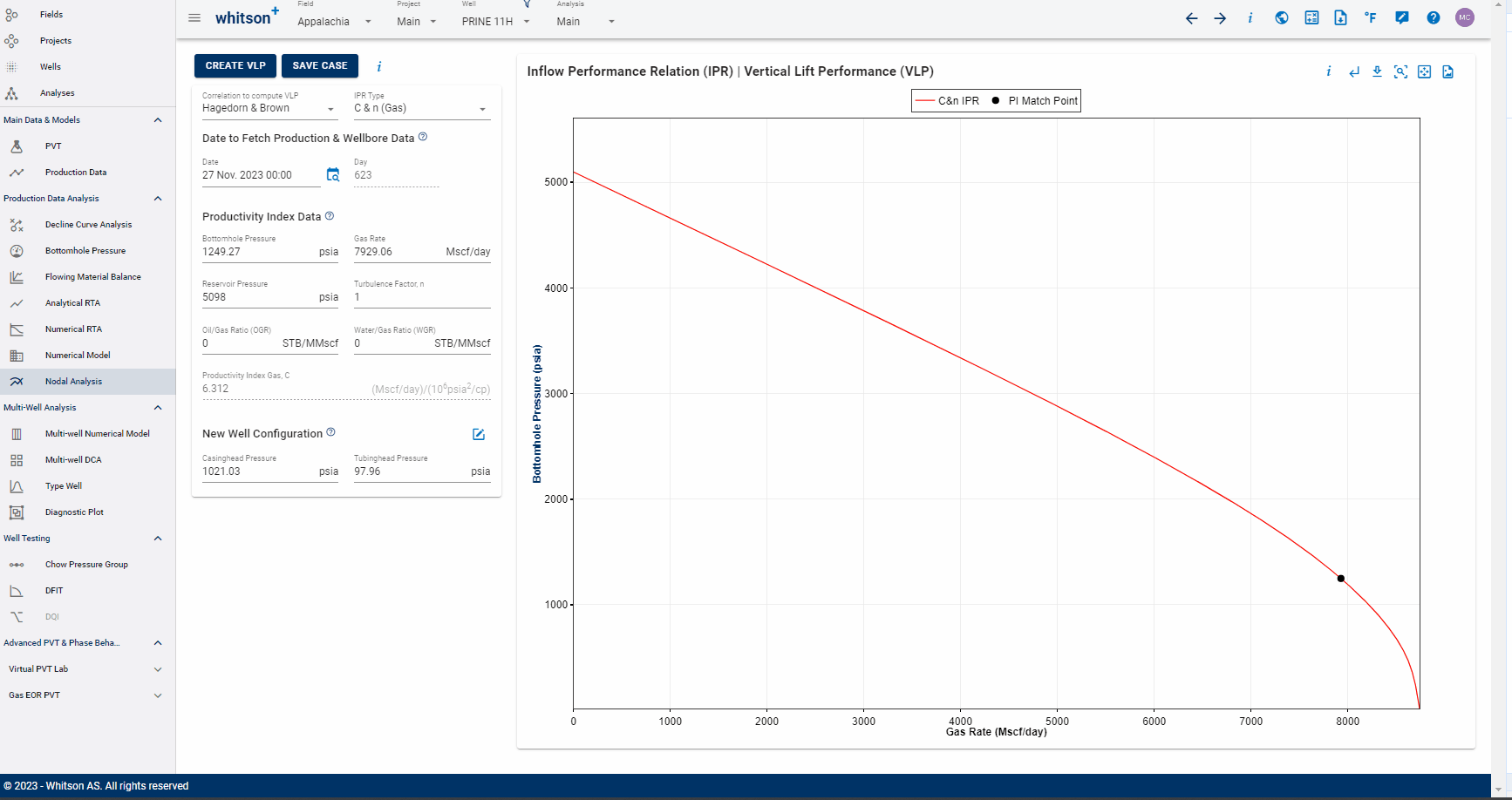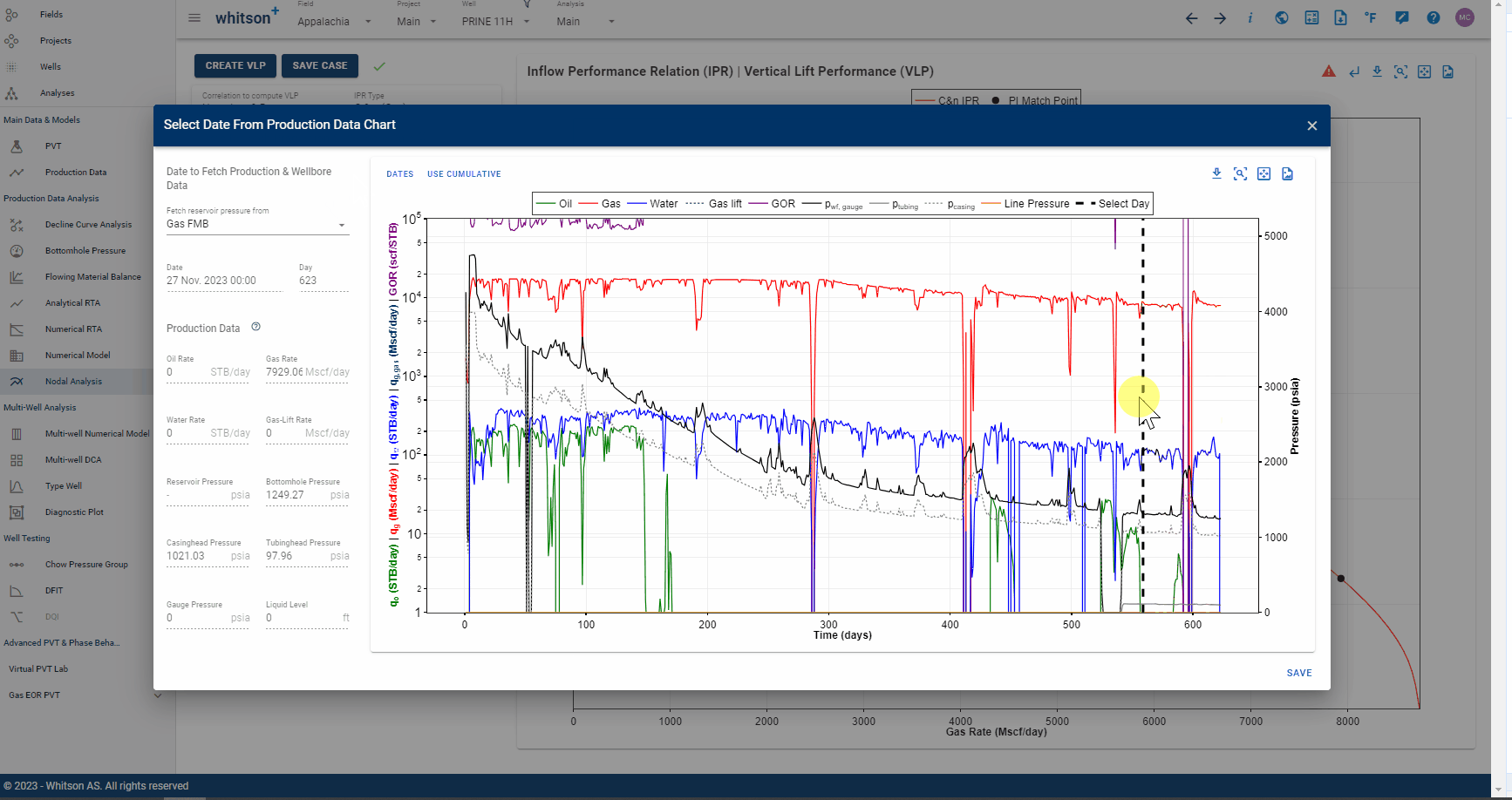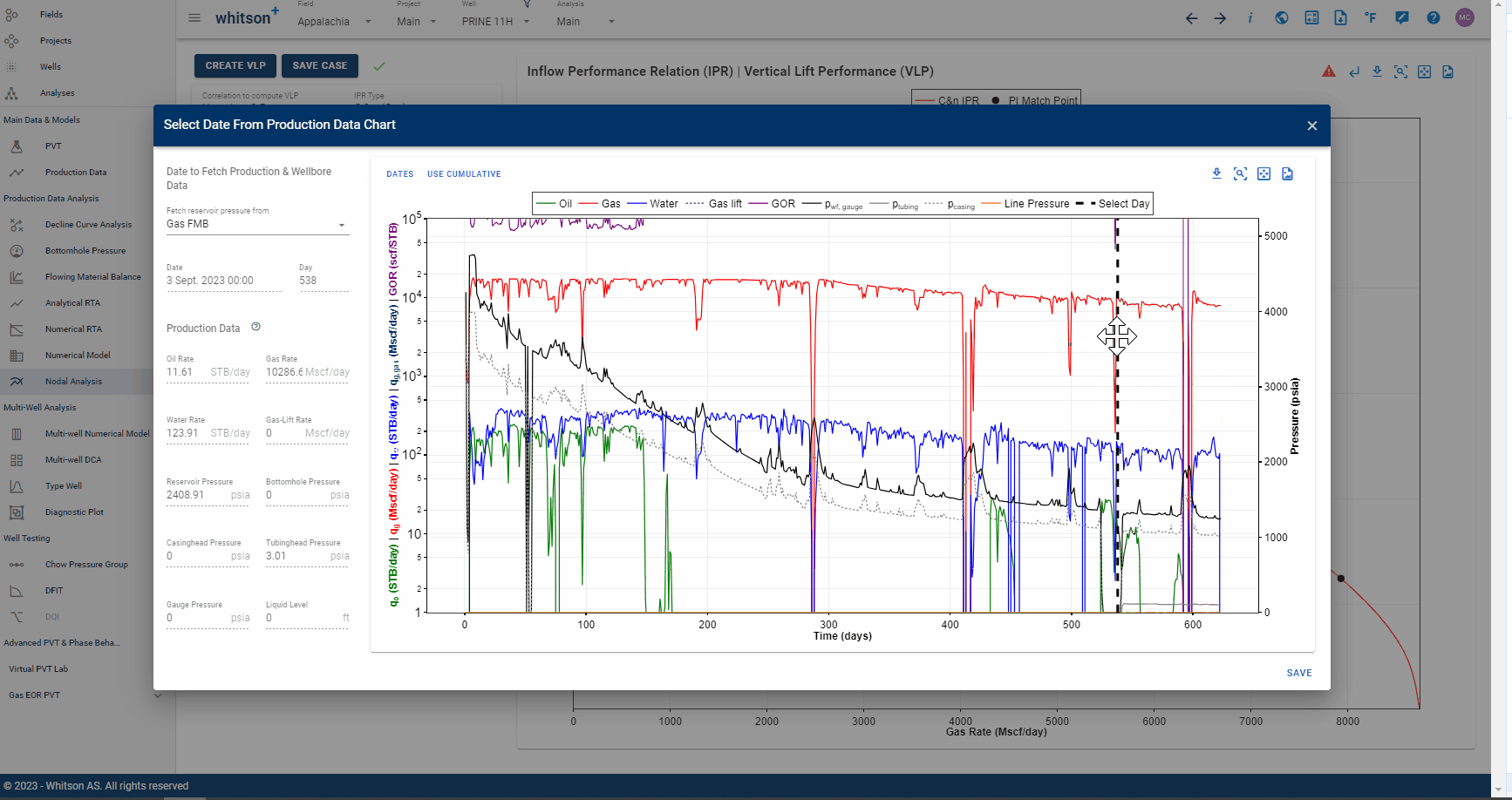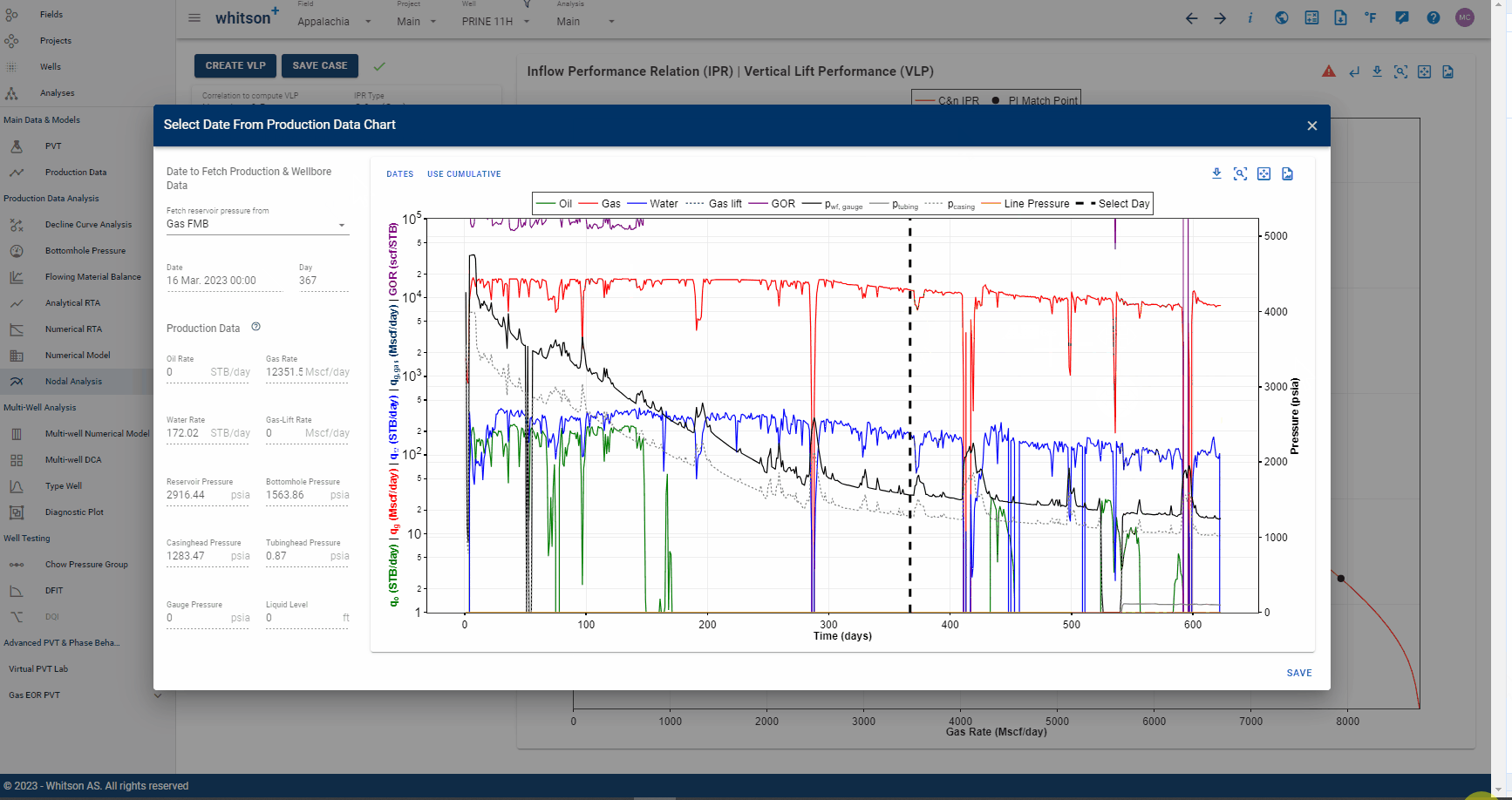
Choose the production test date as shown below. This is used to calculate the Productivity Index, $J$, at a point in time from the well production history.
Selection of the desired date here will automatically populate the Production Data section below with pressures and rates from the well's production history on the selected date.

Next, the Productivity Index Data section is automatically populated from the date selection as follows -

Liquid rate, GOR and WOR are calculated based on the selected production test date input and the associated rates for that date.
BHP is fetched from the Bottomhole Pressure feature
Reservoir pressure is fetched from the multiphase flowing material balance feature.
Saturation pressure is fetched from the PVT feature.

If the BHP, MFMB or PVT analysis is not done for the well, these fields will be blank but the value must be specified manually for the generation of IPR.
The productivity index is calculated at the liquid rate (oil + water) and the specified pressures using the Vogel IPR as outlined above.

1.2 Changing the Wellbore Configuration & Creating VLP

The main intent of this feature is to provide a 'What-if' tool for analyzing different well configurations. The active configuration on the production test date is considered the default or current well configuration and this can be compared against a new wellbore configuration.

Use the New Well Configuration section to set the existing and new well configurations and see them side-by-side which helps comparison of input.
Fix the Casinghead Pressure and Tubinghead Pressure to a constant for both the configurations to generate VLP specific to this combination of parameters.
Once the well configurations are saved, you can choose your favorite BHP correlation to compute the VLP.
Click the 'Create VLP' button on the top-left of the page.

This step generates 2 VLP curves - one for each well configuration which represents the deliverability of the well under each configuration.

The difference in these two VLP curves in terms of where they intersect the IPR provides the difference in stable production rates that can be expected from each of the wellbore configurations by reading off of the liquid rates plotted on the x-axis at the point of intersection.

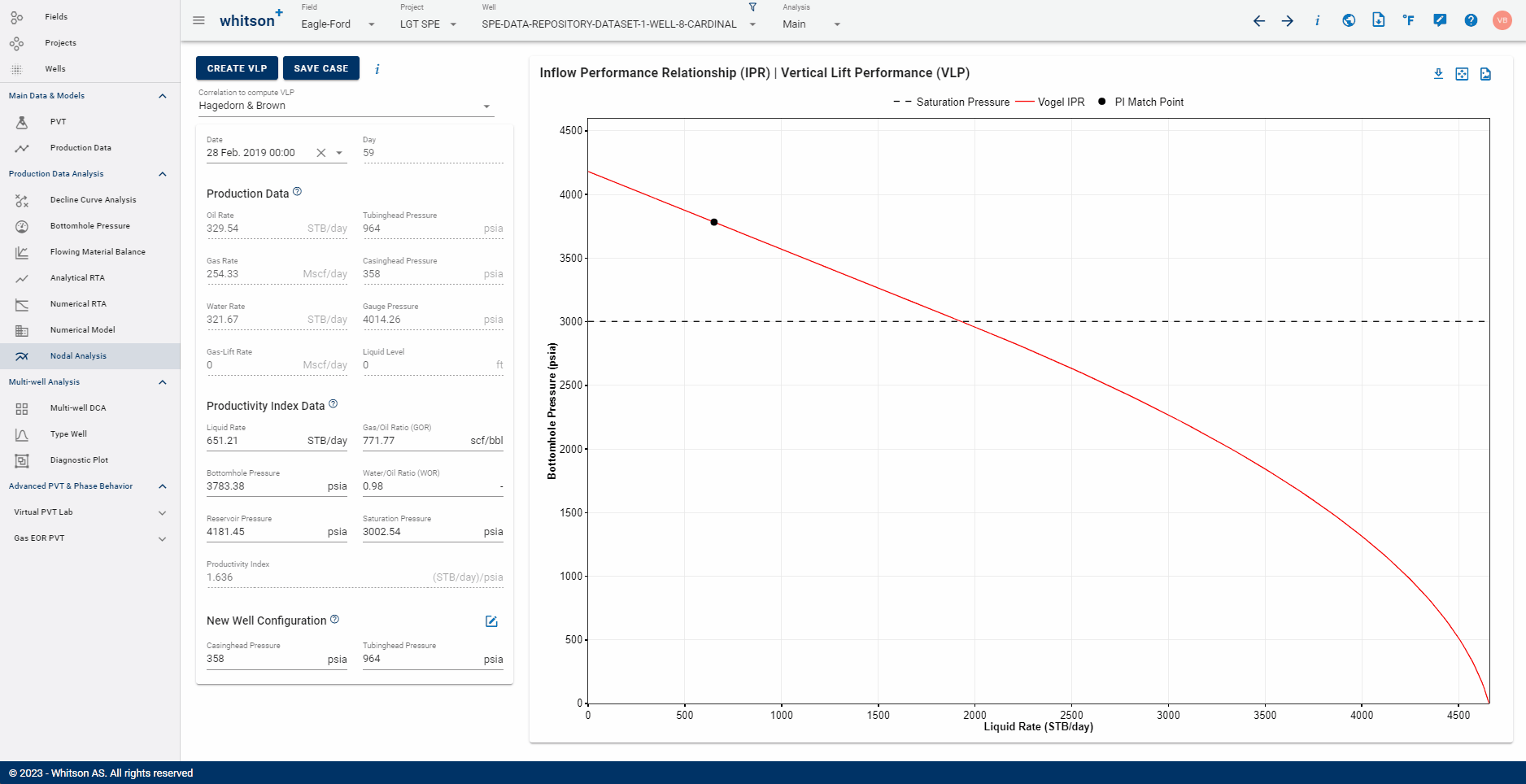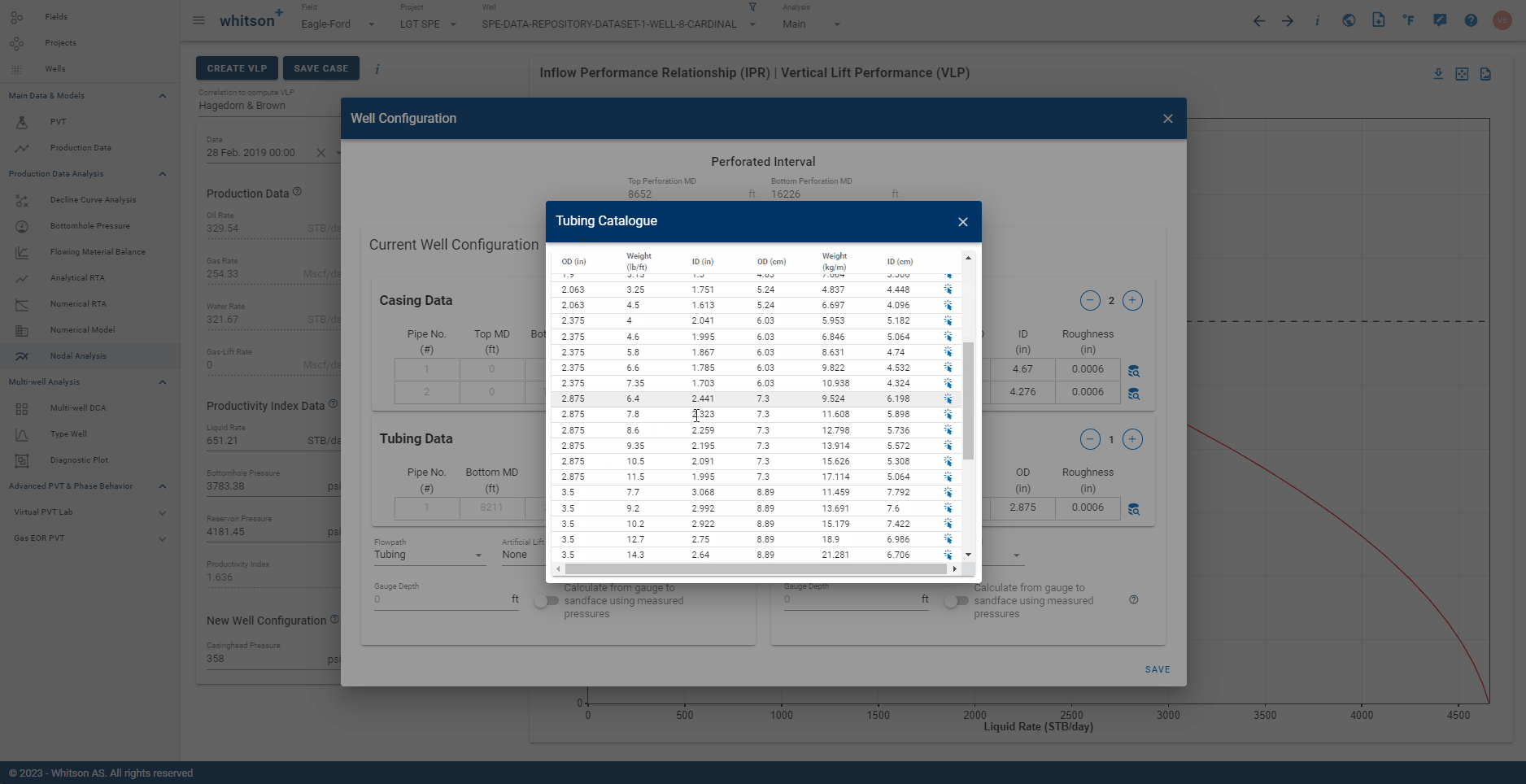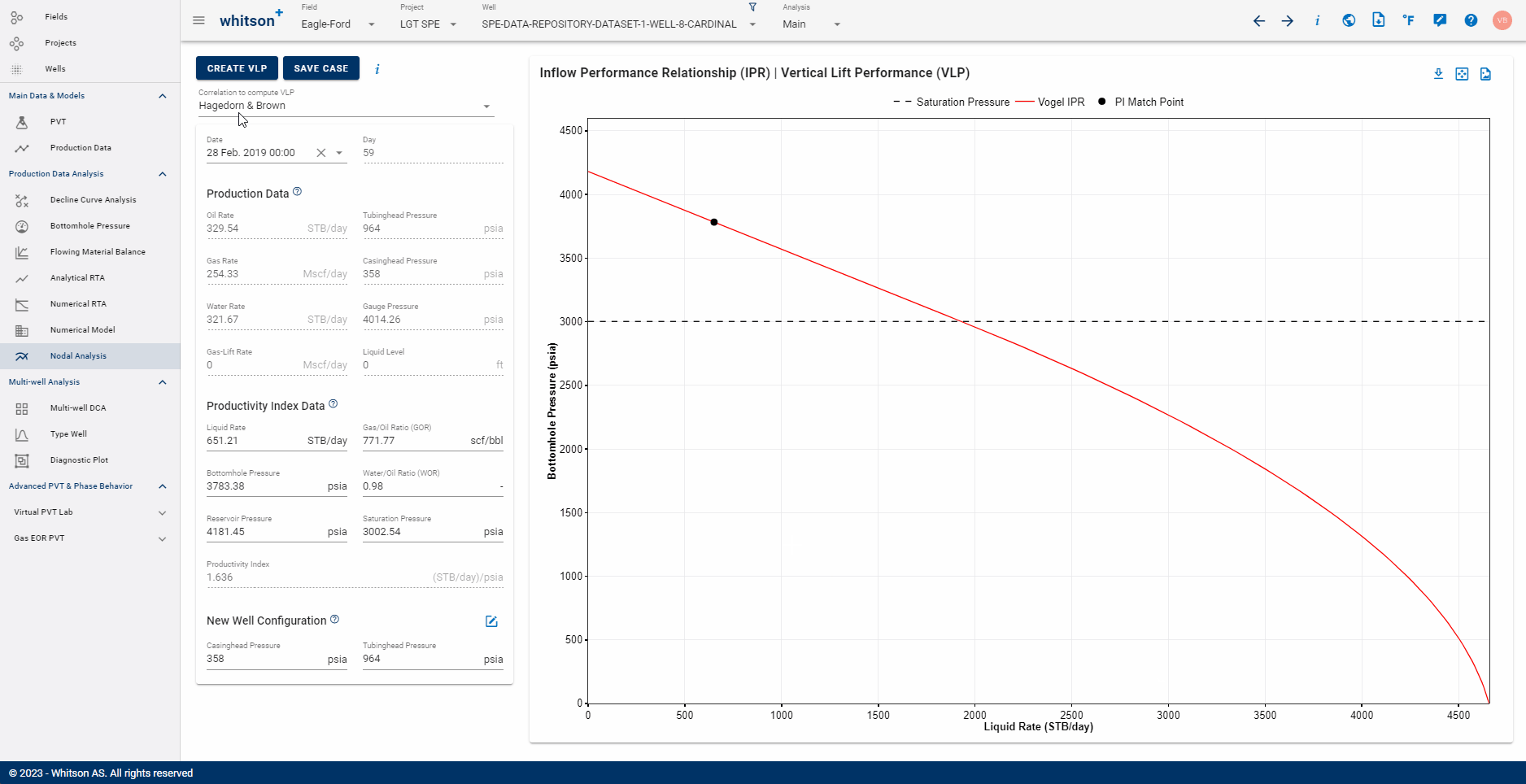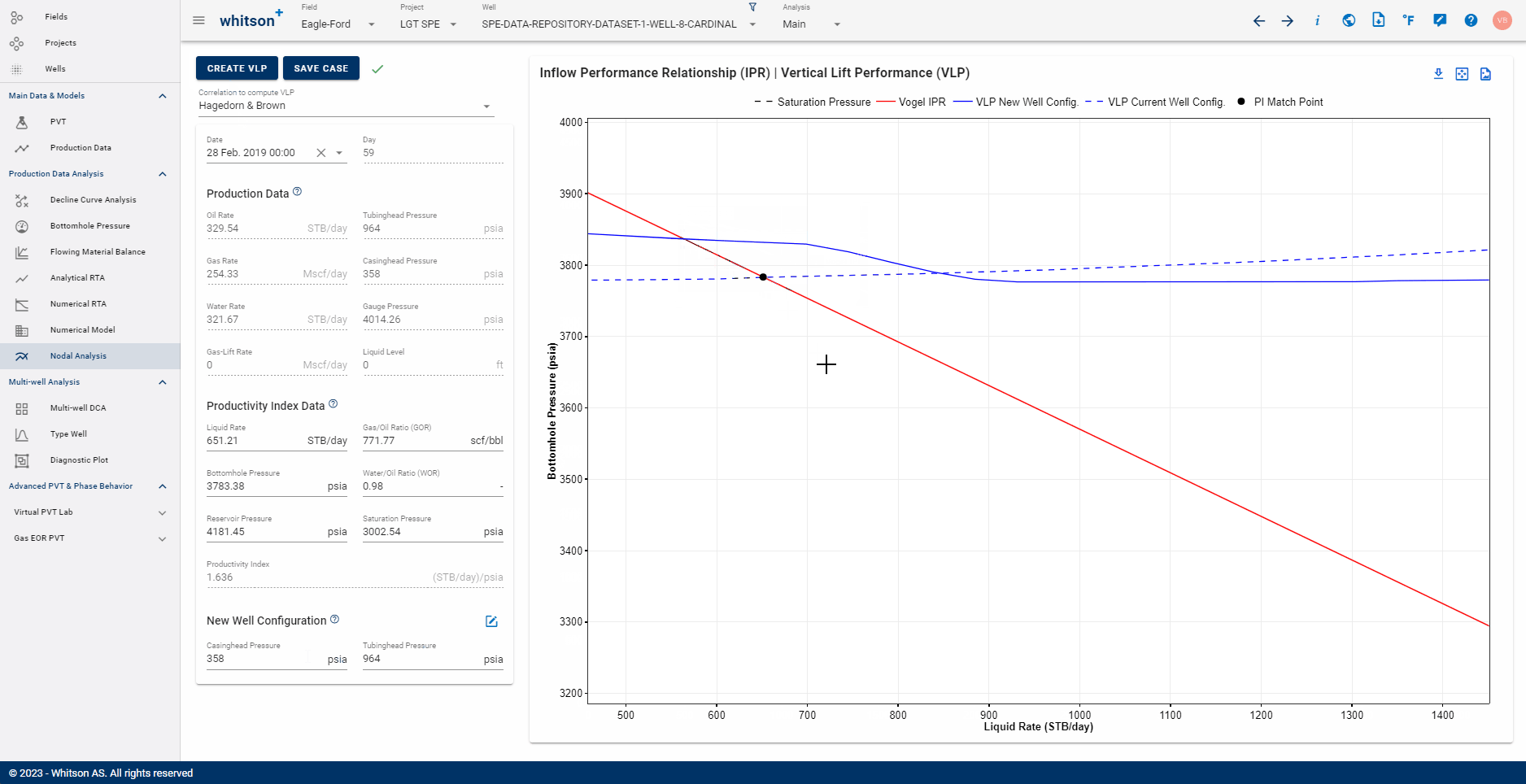
In the example shown in the gif above, we see a 100 STB/D downward revision in production rate if we were to use the highest possible tubing diameter in this well.

1.3 Saving Different Cases

In reality, you may have more than 2 wellbore configurations to choose from for a particular well.
You save each new wellbore configuration independently as a case, allowing us to compare all the different wellbore configurations at once.

To save a case, click 'Save Case' on the top-right. All the saved cases will appear in a new section below all the input.
You can activate the relevant cases in the IPR-VLP plot using the checkbox for each case.

In the example shown in the gif above, we see that the adding gas lift has a more favorable effect compared to changing the tubing configuration in the wellbore.

1.4 IPR and VLP Assumptions

The pseudopressure is rigorously calculated to generate C&n IPR.
A fixed value of $n = 1$ is assumed for the C&n IPR.
"Vogel (Oil + Water)" provides an IPR for surface liquid rate versus pressure. This curve is created from the sum of the Vogel IPR applied to the oil, and a straight line IPR applied to water phase.

1.5 VLP calculations with quiet side option

When using the quiet side for bottomhole pressure (BHP) calculations, a flat vertical lift performance (VLP) in nodal analysis is typically observed. This is due to the assumption that the quiet side represents a single-phase column that is not flowing. In this scenario, the only factor contributing to the pressure drop is the gravity component of the gas column, particularly down to the end of the tubing.

In cases where there is a short distance (less than 100 feet) between the end of the tubing and the top perforation, this small section is the only place where a change in the calculated BHP versus rate will occur. As a result, the VLP appears flat, as it shows the BHP calculated for different rates, and for the quiet side, the BHP is essentially independent of the flowrate.

For more details on how the calculation on the quiet side works, please refer to Static (Quiet) Side

2. Theory

2.1 Reservoir IPR

2.1.1 Straight-Line IPR

The reservoir inflow performance relation (IPR) represents a simple explicit relationship between the surface rate, $q_{\bar{p}}$, of phase $p$, and the flowing bottomhole pressure $p_{wf}$. The simplest IPR is the linear relationship

$\begin{equation} q_{\bar{o}} = J (p_R-p_{wf}) \end{equation}$ where $p_R$ is the average reservoir pressure, $J$ is the productivity index, and $p_{wf}$ can vary in the range $0 \leq p_{wf}\leq p_R$. The lower bound, $p_{wf}=0$, is a theoretical point known as the absolute open flow (AOF) point where $q_{\bar{o}}=q_{\bar{o},max}$. The upper bound, $p_{wf}=p_R$, represents a shut well where $q_{\bar{o}}=0$.

For a vertical well that fully perforates a cylindrically shaped homogenous reservoir, it can be shown, assuming the product $\mu_oB_o$ is only slightly pressure dependent, that the productivity index is equal to $\begin{equation} J=\frac{kh}{141.2\mu_oB_o\big[\ln(r_e/r_w)-3/4\big]} \end{equation}$

2.1.2 Vogel IPR

Oil and Gas Flow

Saturated Reservoir Conditions ($p_R\leq p_{b}$)

The straight-line IPR is only valid for slightly-compressible fluids, such as undersaturated oils and water. For an undersaturated oil, continued production will ultimately bring the average reservoir pressure, $p_R$, below the initial bubblepoint pressure, $p_{b}$, at which gas starts coming out of solution. The free gas phase will make the total compressibility of the system increase rapidly, and the straight-line (slightly compressible fluid) assumption is no longer representative. To account for the release of solution gas, Vogel[1] suggested an IPR on a normalized form:

$\begin{equation} \frac{q_{\bar{o}}}{q_{\bar{o},max}}=1-0.2\bigg(\frac{p_{wf}}{p_R}\bigg)-0.8\bigg(\frac{p_{wf}}{p_R}\bigg)^2 \end{equation}$ Assuming a straight-line IPR, tangent to the Vogel IPR at $p_{wf}=p_R$, it can be shown that the maximum oil rate of the Vogel IPR, $q_{\bar{o},max}$, is: $\begin{equation} q_{\bar{o},max}=\frac{Jp_R}{1.8} \end{equation}$

Undersaturated Reservoir Conditions ($p_{b} < p_R$)

For undersaturated oils ($p_{b}<p_R$), it is normal to combine the straight-line IPR and Vogel IPR in the same plot to show the effect of gas coming out of solution as the flowing bottomhole pressure becomes less than the bubblepoint pressure. To achieve this, the two IPRs are connected at the bubblepoint pressure. The Vogel IPR is used in the pressure range from 0 $p_{b}$, and the straight-line IPR is used in the pressure range from $p_R$ to $p_{b}$. The combined IPR can be expressed as:

$\begin{equation} \label{eq:combined} q_{\bar{o}}= \begin{cases} J(p_R-p_{wf}), &p_{b}<p_{wf}\leq p_R\\ J(p_R-p_{b})+\frac{J*p_{b}}{1.8}\left[1-0.2\left(\frac{p_{wf}}{p_{b}}\right)-0.8\left(\frac{p_{wf}}{p_{b}}\right)^2\right], &0\leq p_{wf}\leq p_{b} \end{cases} \end{equation}$

Oil, Gas, and Water Flow

The Vogel IPR accounts for the effect of released solution gas (i.e., the effect of free gas flowing together with the oil). To get the rates of both phases at a given $p_{wf}$, the oil rate is calculated by the IPR, and the gas rate is calculated by $q_{\bar{g}}=q_{\bar{o}}R_{p}$, where $R_p$ is the producing gas/oil ratio assumed independent of $p_{wf}$. In the case of three-phase flow (oil, gas, and water), the simplest case would be to calculate the water rate from $q_{\bar{w}}=q_\bar{o}F_{wp}$, where $F_{wp}$ is the producing water/oil ratio assumed to be independent of $p_{wf}$.

However, this would lead to the water production behaving as if it has significant gas in solution (curved IPR for the water phase). It is arguably more accurate to handle the water phase separately by it's own straight-line IPR. The liquid-phase (oil + water) IPR will then be the sum of the straight-line IPR for water and Vogel IPR for oil. For an undersaturated oil reservoir with free water flowing, the following is used as the liquid-rate IPR.

$\begin{equation} q_{\bar{L}}=J_w(p_R-p_{wf})+ \begin{cases} J(p_R-p_{wf}), &p_{b}<p_{wf}\leq p_R\\ J(p_R-p_{b})+\frac{J*p_{b}}{1.8}\left[1-0.2\left(\frac{p_{wf}}{p_{b}}\right)-0.8\left(\frac{p_{wf}}{p_{b}}\right)^2\right], &0\leq p_{wf}\leq p_{b} \end{cases} \end{equation}$

Here an example that compares the results of manual calculations using these equations with those obtained from whitson+
Vogel IPR Curve Calculation Example

2.1.3 C&n IPR

Pressure-Squared Approximation

The Vogel IPR is applied to fluid systems that initially are undersaturated oils. For fluid systems that initially are gases, the C&n IPR, sometimes refered to as the "back-pressure equation", is used.

Rawlins and Schellhardt[2] performed multirate deliverability tests on over 500 gas wells and noted that the difference between the average reservoir pressure squared and the flowing bottomhole pressure squared (i.e. $p_R^2 - p_{wf}^2=\Delta p^2$) plotted against the corresponding stabilized flow rates produced a straight line in a log-log plot. Hence, the IPR was suggested to be

$\begin{equation} \label{eq:gasIPRC&n} q_{\bar{g}} = C\left(p_R^2 - p_{wf}^2 \right)^n \end{equation}$

The exponent $n$ represents the effect of high-velocity inflow to the well (i.e, the effect of non-Darcy turbulent flow)

$n=1$ for when the flow is characterized by Darcy's equation.
$0.5 \leq n \leq 1$ for when the flow is characterized by Non-Darcy effects, turbulence.

The coefficient $C$ is a measure of deliverability accounting for primarily the drainage area and permeability.

Fetkovich[4] argued that the pressure-squared C&n IPR could also be used for saturated oils, as it is very similar to the Vogel IPR equation for $n = 1$. The C&n equation with $n=1$ can be written as

$\begin{equation} \frac{q_{\bar{o}}}{q_{\bar{o},max}}=1-\bigg(\frac{p_{wf}}{p_R}\bigg)^2 \end{equation}$

which results in an IPR that's a little more conservative than Vogel's. Field data may often be matched equally good to both IPRs, making the C&n equation are a more general IPR as it may be applied to both saturated oils and gases.

Well-test procedures for determining $n$

The multirate tests used to generate the straight line plots in log-log pseudopressure vs rate consists a series of pressure vs rate measurements which may be -

Flow-after-flow tests - Producing the well at stabilized flow rates and pressures. Rawlins and Schellhardt used this but it may be practically impossible to test the well long enough to obtain stabilized data for low-permeability gas wells.
Isochronal tests - Producing the well at different flow rates with flowing periods of equal duration. Each flow period is separated by a shut-in period long enough to allow the bottomhole pressure to stabilize at the average reservoir pressure (again, not possible in low-permeability reservoirs). Also needs an extended stabilized flow point.
Modified isochronal tests - Overcomes the limitation of obtaining stabilized data for low-permeability wells by modifying the isochronal test to require shut in periods longer than or equal to the flow periods separating them. Less accurate compared to isochronal testing.
Transient tests - Requires estimates of drainage area and shape, additional reservoir and fluid properties and is hence complex but it eliminates need for stabilized data.

Such high quality multirate test data is rarely available for all the wells so it may be hard to determine the deliverability exponent. It has been shown by Golan and Whitson[3] and field data from gas wells that the value of n only varies slowly and can be assumed to be roughly constant over the life of the well to simplify calculations and avoid the use of rock and fluid properties to estimate future deliverability.

Rigourous Handling with Pseudopressure

Gas well performance through the pressure-squared approximation is only valid at low reservoir pressures. To rigorously calculate the flow at all pressures, it is required to use the pseudopressure defined as:

$\begin{equation} m(p) = 2\int_0^p \frac{p'}{\mu_gZ}dp' \end{equation}$

In the C&n IPR, the pressure-squared terms are simply replaced by the pseudopressure, yielding

$\begin{equation} \label{eq:gasIPRC&npseudop} q_{g} = C\left(m(p_R) - m(p_{wf})\right)^n \end{equation}$

Non-dimensional form of the backpressure equation using AOF rate

This backpressure equation is written in normalized form with AOF rate, squared-pressures to develop the IPR equation for gas wells in dimensionless form as

$\begin{equation} \label{eq:gasipr} \frac{q_{g}}{q_{g,max}} = \left(1 - \left( \frac{p_{wf}}{p_R} \right)^2 \right)^n \end{equation}$

We can write the same equation in terms of gas pseudopressures as:

$\begin{equation} \label{eq:gasiprpp} \frac{q_{g}}{q_{g,max}} = \left(1 - \left( \frac{p_p(p_{wf})}{p_p(p_R)} \right) \right)^n \end{equation}$

Note on Constant Productivity Index, $J$ and stable inflow performance

Stable inflow performance—constant $J$—requires the condition of pseudosteady-state (PSS) / boundary-dominated flow. Simply stated, PSS represents the condition when the entire drainge volume of the well contributes to production. In high permeability formations, this may happen instantaneously but in low permeability formations, the flow may be infinite acting for years in which case, expecting a stabilized IPR is not practical. If the reservoir has not reached PSS yet, then both $J$ and $C$ will be time-dependent and consequently keep shrinking the IPR envelope towards the origin until stable values are achieved.

2.3. Calculating the Well PI

To compute IPR of a well, it is necessary to provide a test point $(q_{\bar{j},test}, p_{wf,test})$ for phase $j$ to compute the productivity index $J$ for the Vogel IPR, and the deliverability constant $C$ for the C&n equation.

2.3.1 Vogel (Oil + Water) PI

For oil phase using the Vogel IPR, the productivity index $J_o$, may be calculated in a few different ways, depending on the conditions of the test point.

If the test occurs at the conditions $p_{bi}<p_{wf,test}<p_R$, then $J_o$ is computed from first definition of the combined IPR in Eq. (\ref{eq:combined})

$\begin{equation} \label{eq:Jabvpb} J_o = \frac{q_{\bar{o},test}}{p_R - p_{wf,test}} \end{equation}$

If the test occurs at the conditions $p_{wf,test}<p_{bi}<p_R$, then $J_o$ is computed from the second definition of the combined IPR in Eq. (\ref{eq:combined})

$\begin{equation} \label{eq:Jbelpb} J_o = \frac{q_{\bar{o},test}}{p_R - p_{bi} + \frac{p_{bi}}{1.8}\big[ 1 - 0.2\big(\frac{p_{wf,test}}{p_{bi}}\big) - 0.8\big(\frac{p_{wf,test}}{p_{bi}}\big)^2 \big]} \end{equation}$

For the water phase, the test point $(q_{\bar{w},test},p_{wf,test})$ is used to compute the water PI, $J_w$, from a straight-line IPR $\begin{equation} J_w=\frac{q_{\bar{w},test}}{p_R-p_{wf,test}} \end{equation}$

The liquid rate as a function of flowing bottomhole pressure is then computed as: $\begin{equation} q_{\bar{L}}(p_{wf})=q_{\bar{o}}(p_{wf})+q_{\bar{w}}(p_{wf}) \end{equation}$

2.3.2 C&n (Gas) PI

For the gas phase using the C&n IPR, the deliverability constant $C$, is calculated by

$\begin{equation} C = \frac{q_{\bar{g},test}}{m(p_R)-m(p_{wf,test})} \end{equation}$ where we have assumed $n=1$. If $n$ is unknown too, then at least two test points are required.

2.4. Well VLP

The Vertical Lift Performance, VLP (also referred to as Tubing Performance Relationship, TPR) describes the pressure drop associated with lifting the fluid at a given rate through the given wellbore configuration at fixed tubing head pressure or casing head pressure.

The VLP takes into account the following pressure elements at the bottomhole, across the range of possbible production rates, to determine the deliverability of the well in combination with what the reservoir can deliver (i.e. the IPR) -

Backpressure exterted at the surface from the choke and wellhead assembly—Wellhead pressures
Hydrostatic pressure due to gravity and the elevation change between the wellhead and the intake to the tubing—Fluid properties and deviation survey
Friction losses, which may include irreversible pressure losses due to viscous drag and slippage—Current or planned wellbore configuration and rates

The VLP is only valid for a specific set of well data.

Changing wellhead pressure, gas/liquid ratio, i.e PVT, or tubing dimensions in wellbore configurations will change the VLP and will require the construction of a new curve.

If the tubing intake pressure calculated from the VLP intersects the bottomhole pressure from the IPR curve, the rate at the point of intersection determines the deliverability of the well and this is the rate of natural, stable flow that can be expected from the particular well in this configuration.

The point of intersection gives the natural flow rate by reading off of the rate axis on the nodal analysis plot.

If there is no intersection, the given backpressure and wellbore configuration will be unable to naturally deliver the fluid to the surface from the tubing intake.

What if my IPR and VLP intersect in two places?

This is likely for certain multiphase mixtures and configurations. One represents a stable flow condition and the other is an unstable one. Mathematically, the stable point of natural flow exists when the two performance curves intersect with slopes (derivatives) of opposite sign.If the two performance relations intersect with slopes at the point of intersection of similar sign, the well is in unstable equilibrium and only a small change in rate may cause the system to change it's state of equilibrium, either killing the well or moving it toward the stable point of natural flow.

3. References

[1] Vogel, J.V.. "Inflow Performance Relationships for Solution-Gas Drive Wells." J Pet Technol 20 (1968): 83–92.

[2] Rawlins, E.L. and Schellhardt, M.A. 1935. Backpressure Data on Natural Gas Wells and Their Application to Production Practices, 7. Monograph Series, U.S. Bureau of Mines.

[3] Golan, M. and Whitson, C.H. 1991. Well Performance, second edition. Englewood Cliffs, New Jersey: Prentice-Hall Inc.

[4] Fetkovich, M. J.: "The Isochronal Testing of Oil Wells," paper SPE 4529 presented at the SPE 48th Annal Meeting, Las Vegas, Sept. 30-0ct. 3, 1973.