Multiphase Flowing Material Balance
1. Practical use
1.1 Multiphase FMB in a nutshell
The multiphase FMB method can be summarized as,
- Plotting technique to analyze multiphase production data.
- Outputs contacted pore volume (Vp, OOIP, OGIP, OWIP).
- Requires PVT, production data, bottomhole pressures and initial reservoir conditions.
- Does not require relative permeability.
- Assumes boundary dominated flow, but can still be used for infinite acting flow.
- Used to bound RTA.
- Can be used to evaluate Refracs - for improvement in contacted pore volume after the Refrac.
- Developed by Leslie Thompson & Barry Ruddick (2017-2022).
Key Benefits,
- It's very fast to run and a good way to get a lower contacted OOIP number. In many cases, it can be beneficial to have a lower estimate of the pore volume, especially in wells with noisy data or before determining accurate \(F_{cd}\), relative permeability, etc., in the numerical model.
- It can also be used to QC the \(S_{wi}\) assumption.
- If build-up data is present, it can almost be used as a well test. Back-calculated pavg must be larger than pwf during build-up. It provides a great lower bound for pore volume (agnostic to rel. perm, \(F_{cd}\)).
- It is not an iterative method, so it can be used to compare wells against each other to compare pore volumes.
1.2 Contacted Pore Volume (Vp)
Fig. 1: In-place volume (grey) vs contacted pore volume (blue)
This feature outputs contacted pore volume, which is the pore volume the well has been able to "contact" after completion. This should not be confused with mapped in-place volumes, which typically is much higher. The contacted pore volume is sometimes referred to as the stimulated rock volume (SRV) and drained rock volume (DRV). When quantifying the contacted pore volume all of the following are used interchangably as they are a function of eachother (connected through PVT and Swi); Vp, OOIP, OGIP and OWIP.
1.3 Which slope to pick?
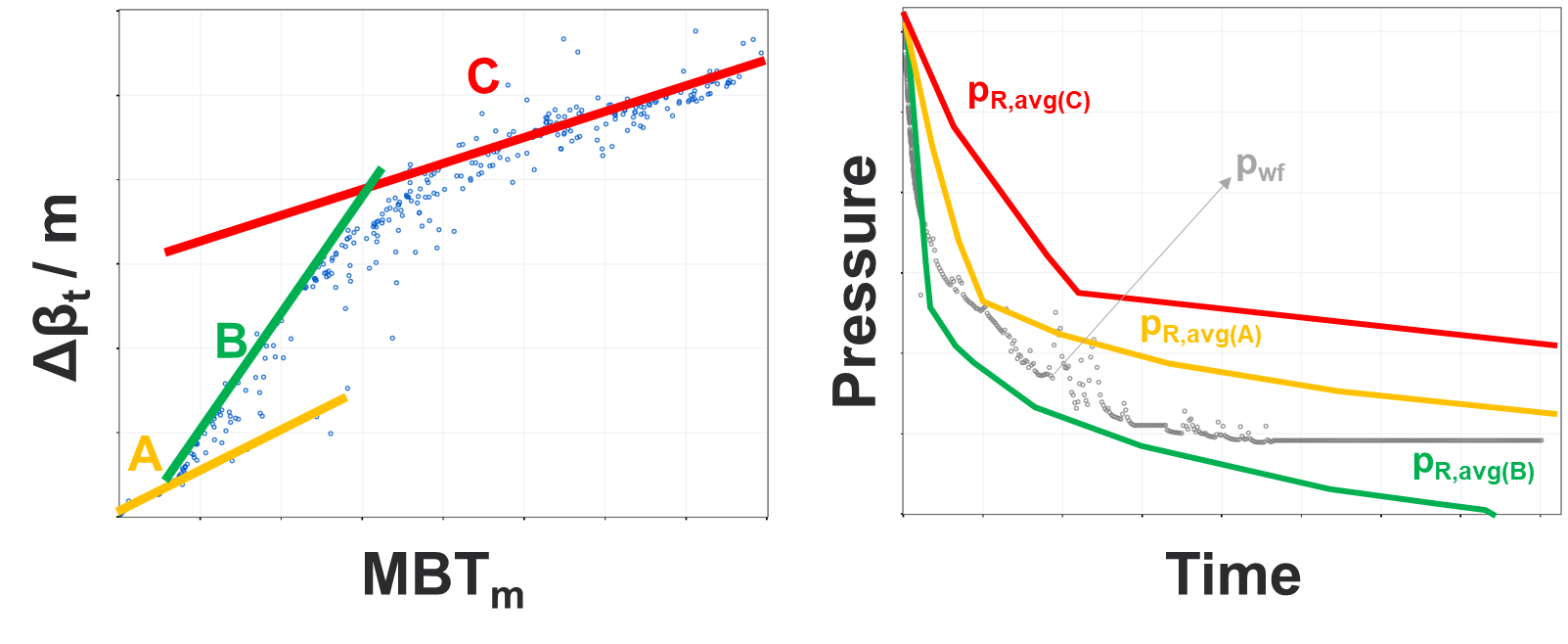
Fig. 2: Pick shallowest observed slope
In real field data, one can observe several slopes on the multiphase FMB diagnostic plot. In general, you should pick the shallowest observed slope i.e., the “largest contacted pore volume observed”. Each slope will yield a different reservoir pressure versus time curve, and should at minimum honor that pavg > pwf at all points in time.
1.4 Build-up data present
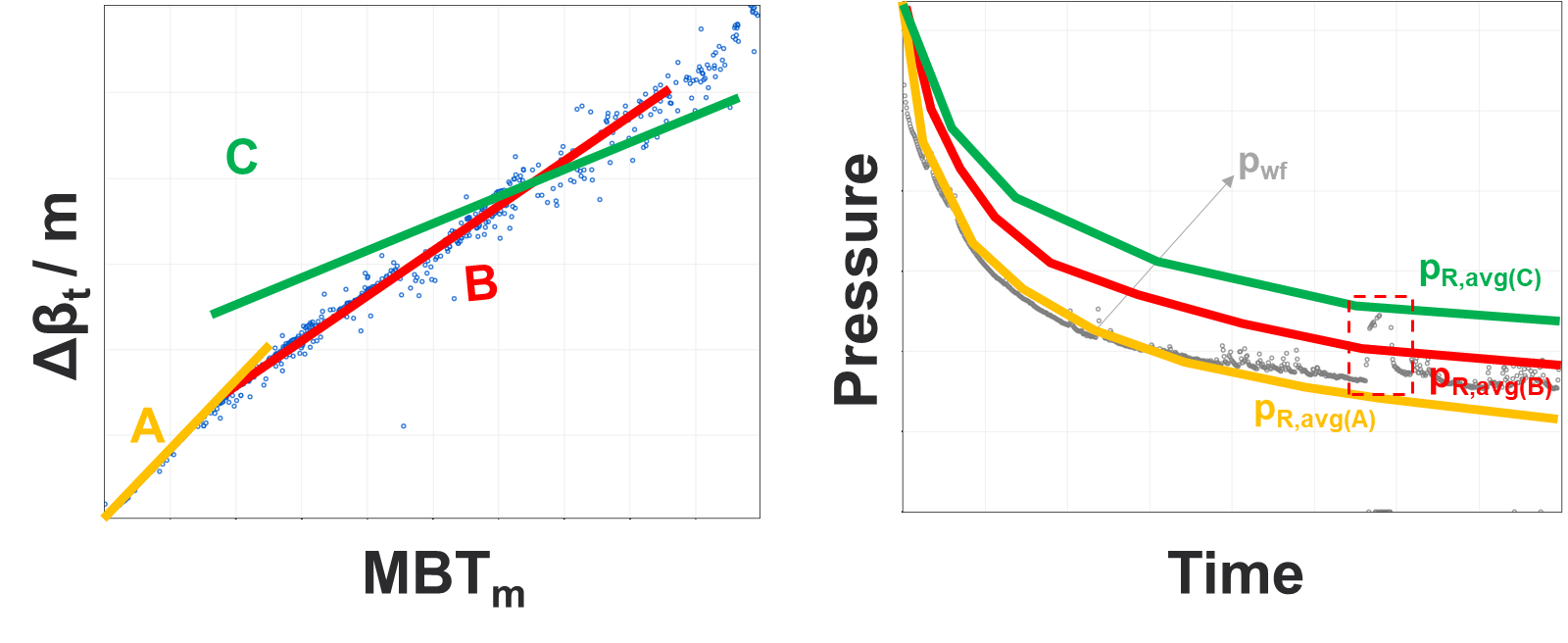
Fig. 3: Good build-up data should always be honored.
If buildup data is present, adjust the slope until it just honors the buildup data. This slope might be shallower (i.e., “larger contacted pore volume”) than what the depletion data only suggests. If a frac hit (“bash”) is observed, and the reason for the pressure build-up, this part of the data should be ignored.
1.5 What if my well is still infinite acting (IA)?
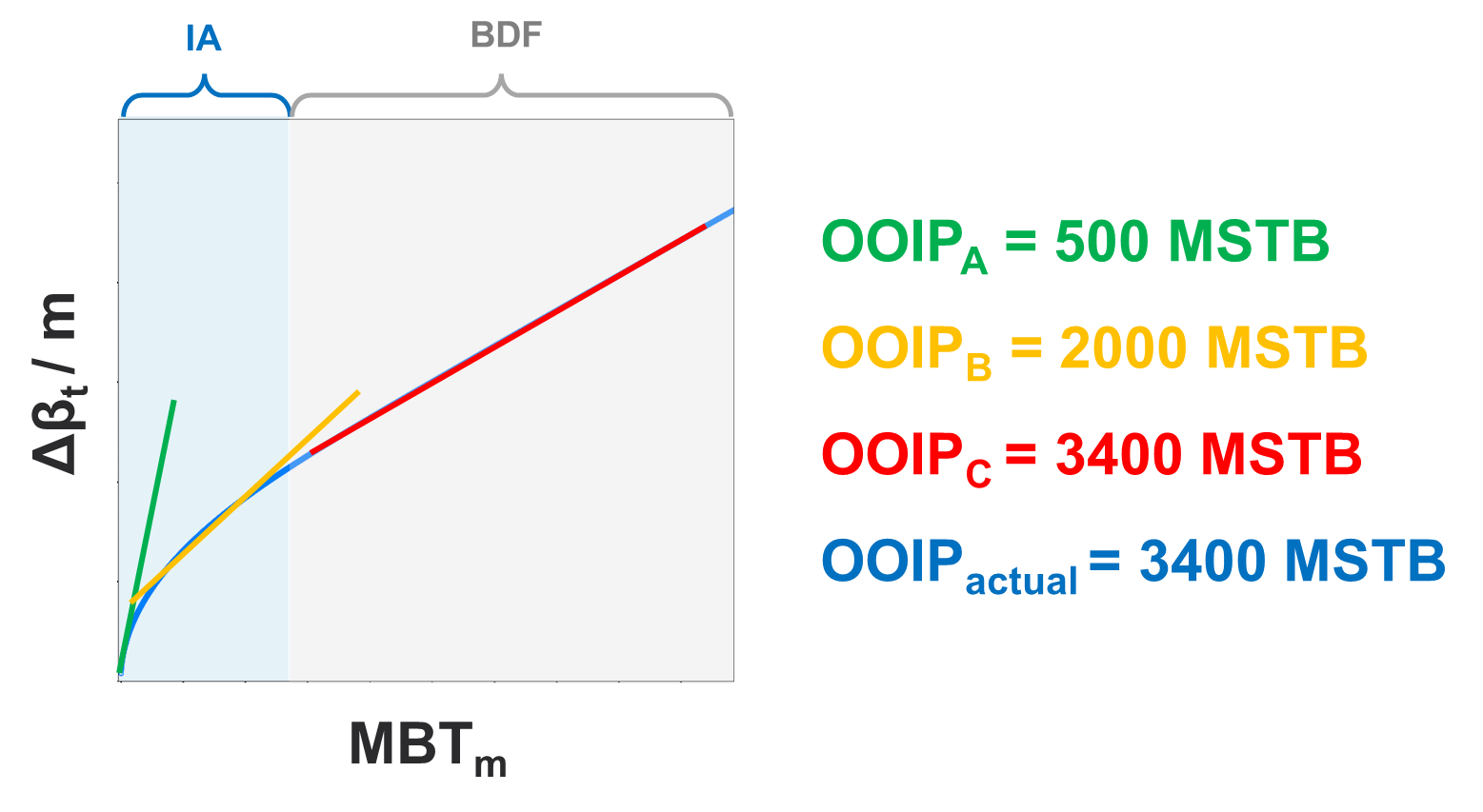
Fig. 4: An well in infinite acting flow (IA) will provide an conservative estimate Vp.
If well is still infinite acting (IA), multiphase FMB provides a conservative estimate of contacted pore volume (OOIP | OGIP | OWIP). Numerical, or analytical, RTA can be used to evaluate if the well is still infinite acting.
1.6 Exclude water in Multiphase FMB
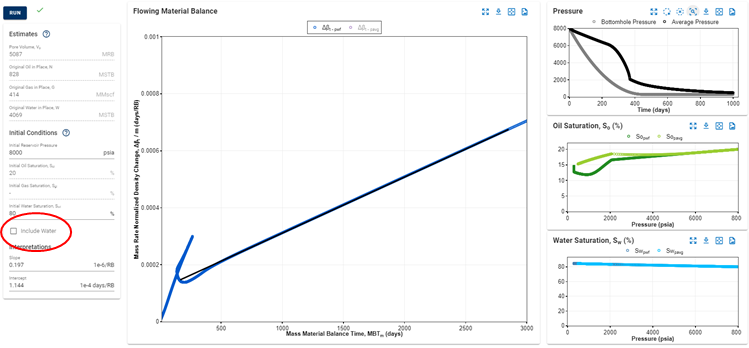
Fig. 5: Excluding water from the MFMB analysis.
There is an option in the software to exclude the water, which will always result in a more conservative OOIP/OGIP estimate.
So why run it?
- It provides a lower estimate of OOIP/OGIP, hence good for bracketing of contacted pore volumes.
- Measurement of water rates can be subject to lots of uncertainty, hence removing water can clean up the diagnostic plot / trend.
- If all, or parts, of the water production comes from a water layer (fraced into), it makes sense to remove the water to analyze the hydrocarbon bearing formations only.
1.7 MFMB Integral: Reducing Noise
Integral analysis reduces the noise, but also reduces the signal.
There is an option to plot the "MFMB integral". See gift below-
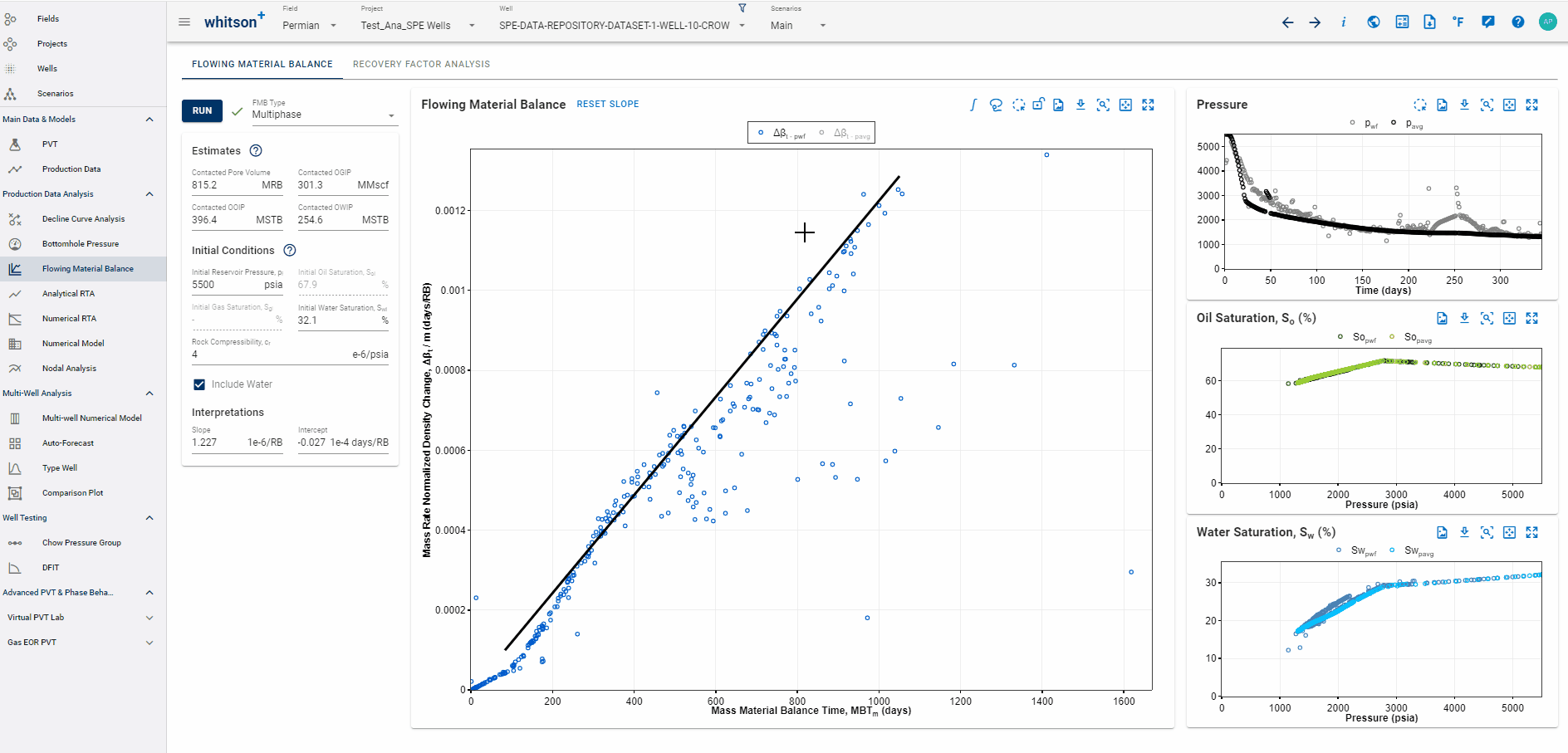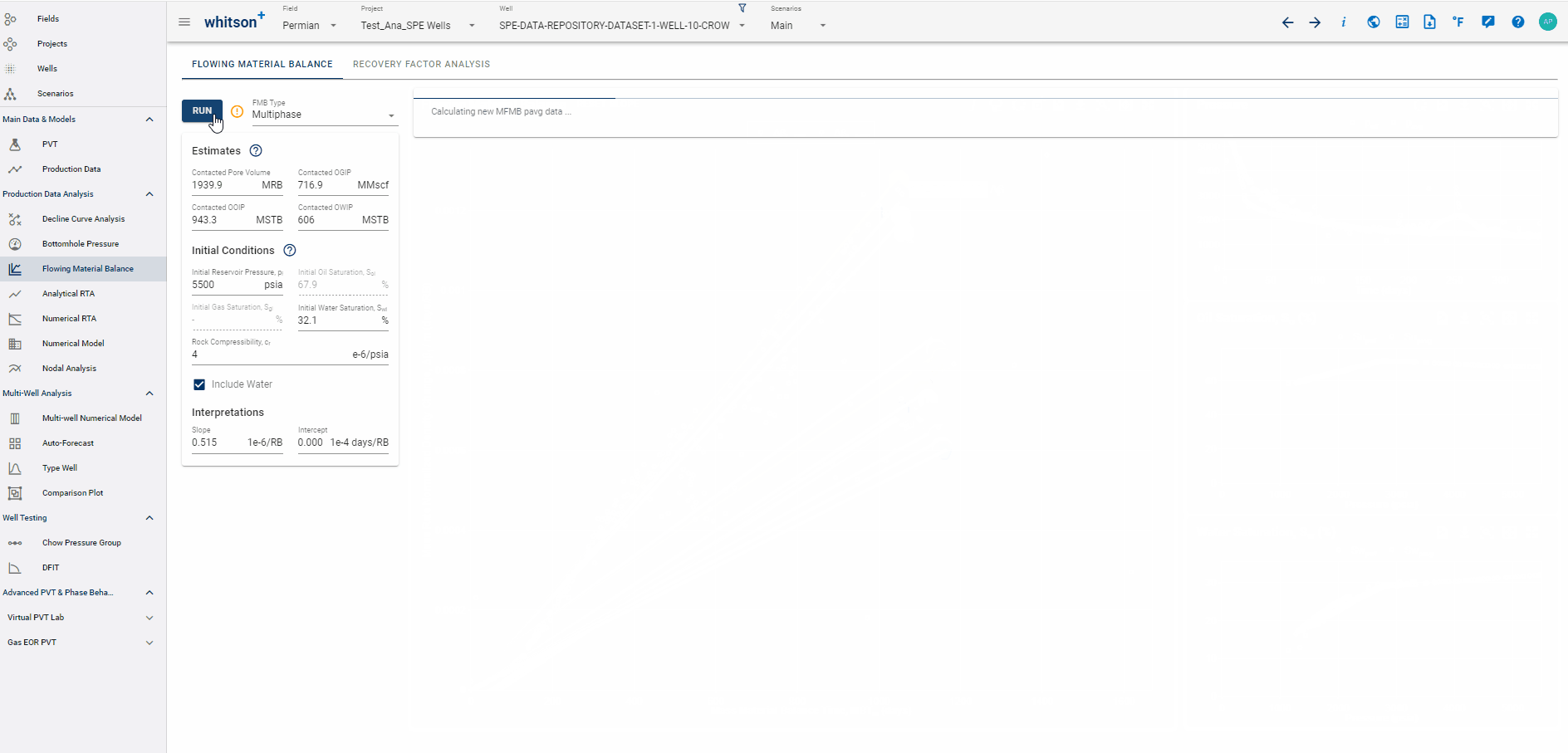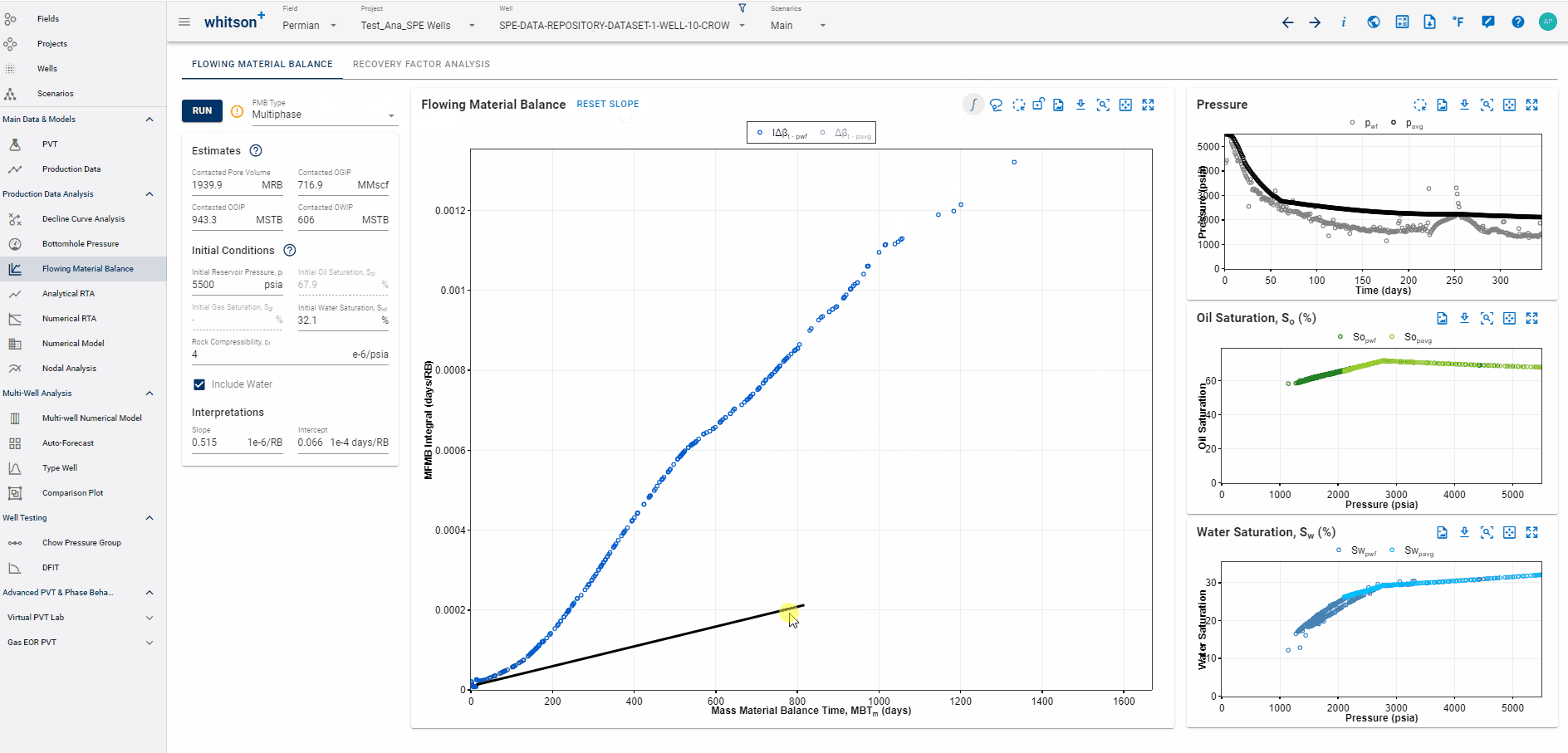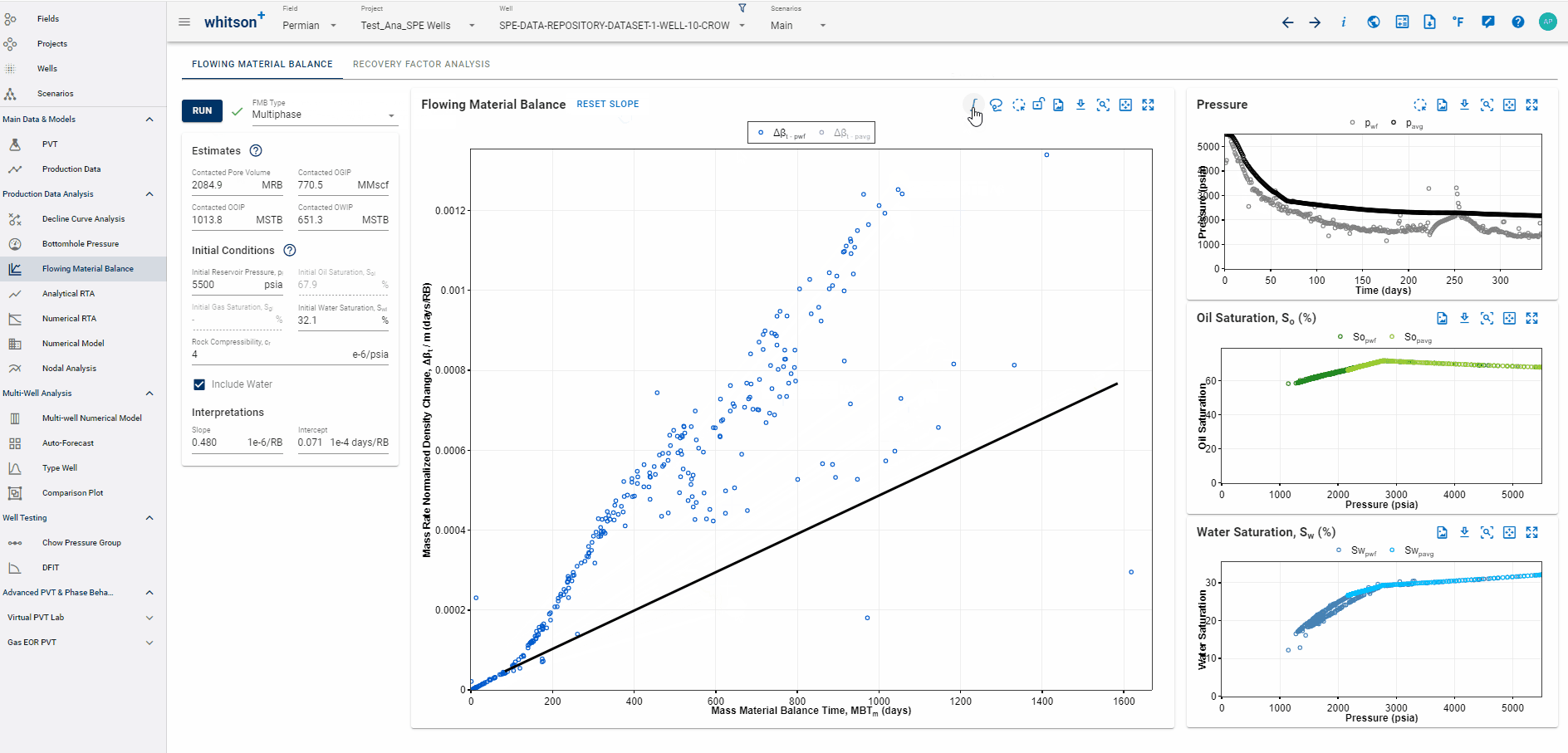
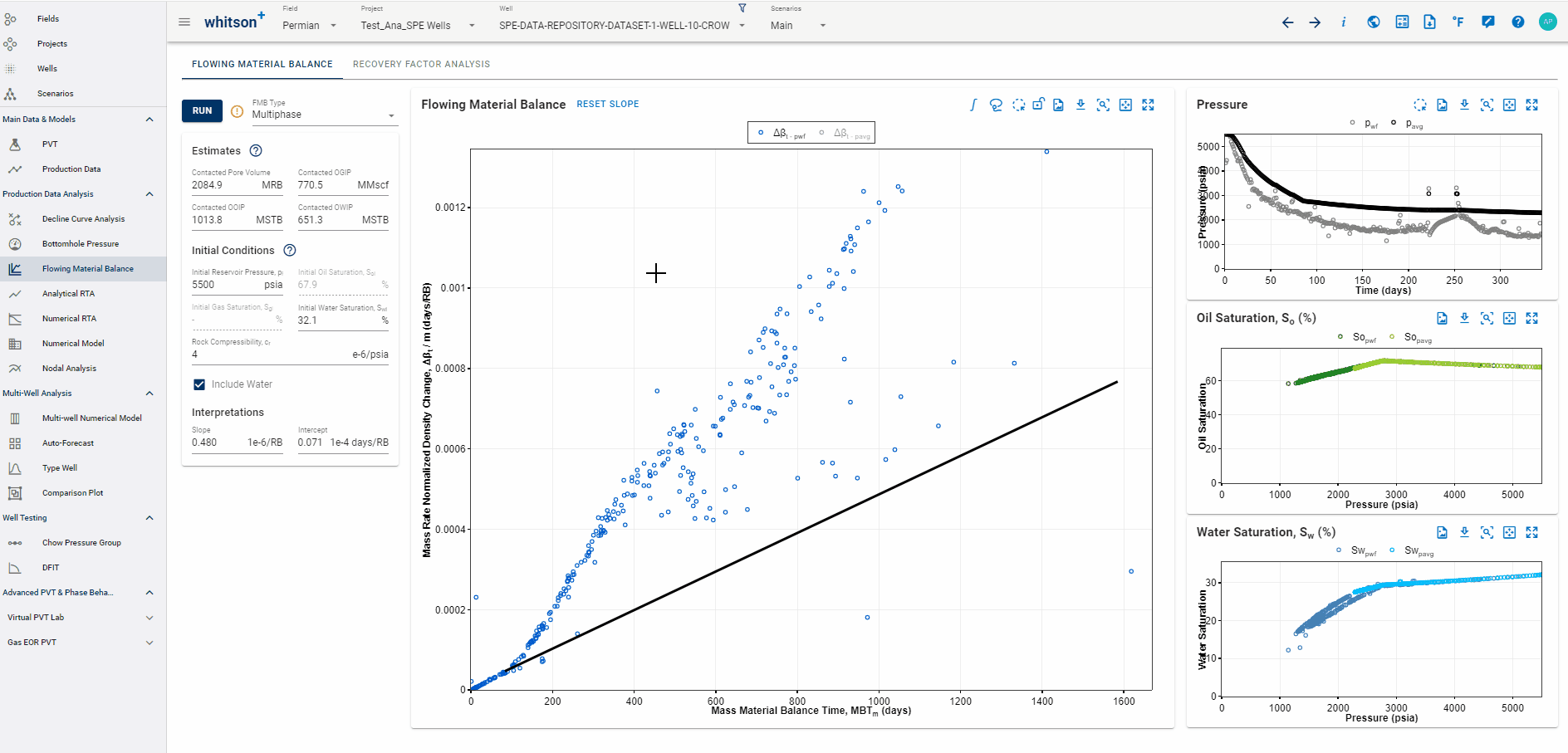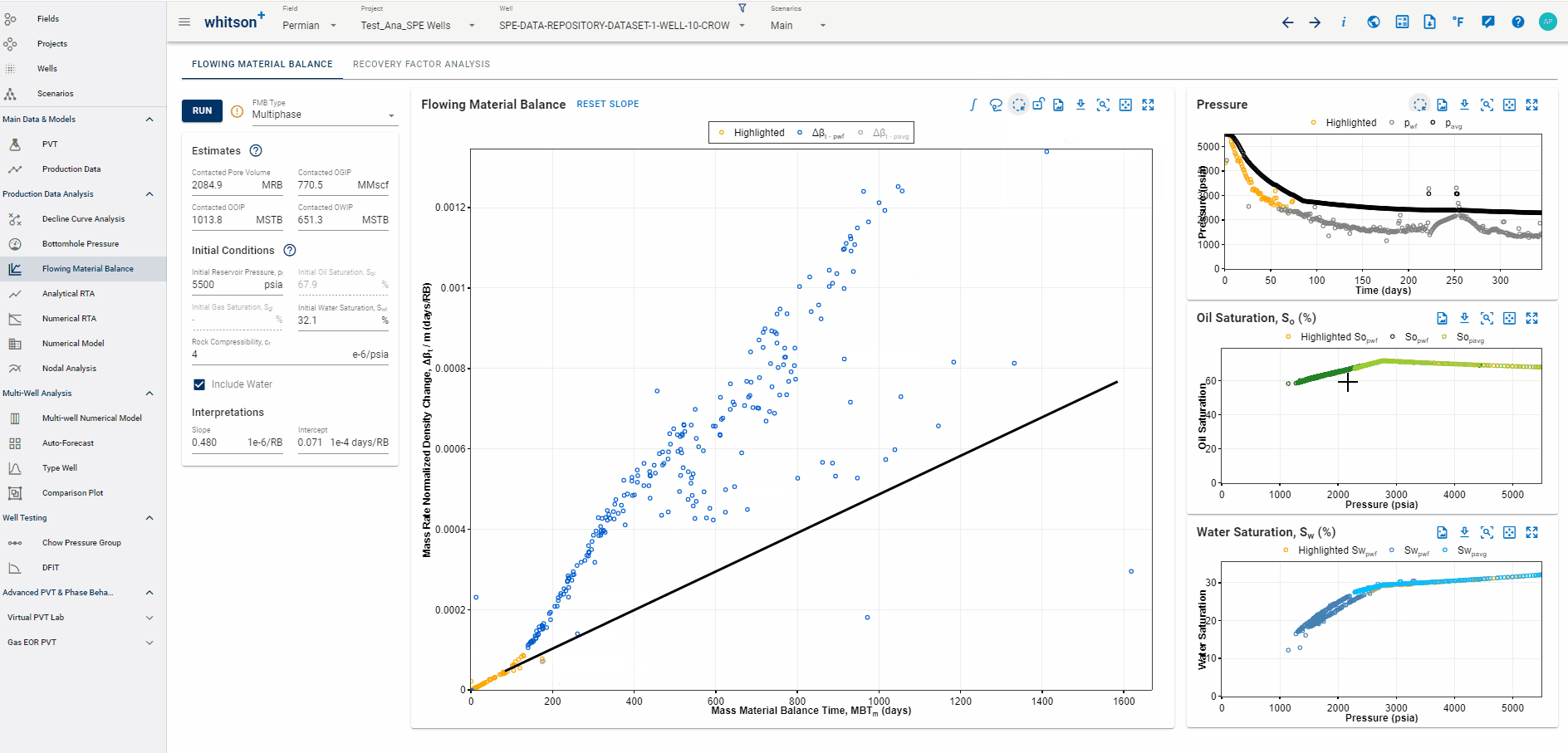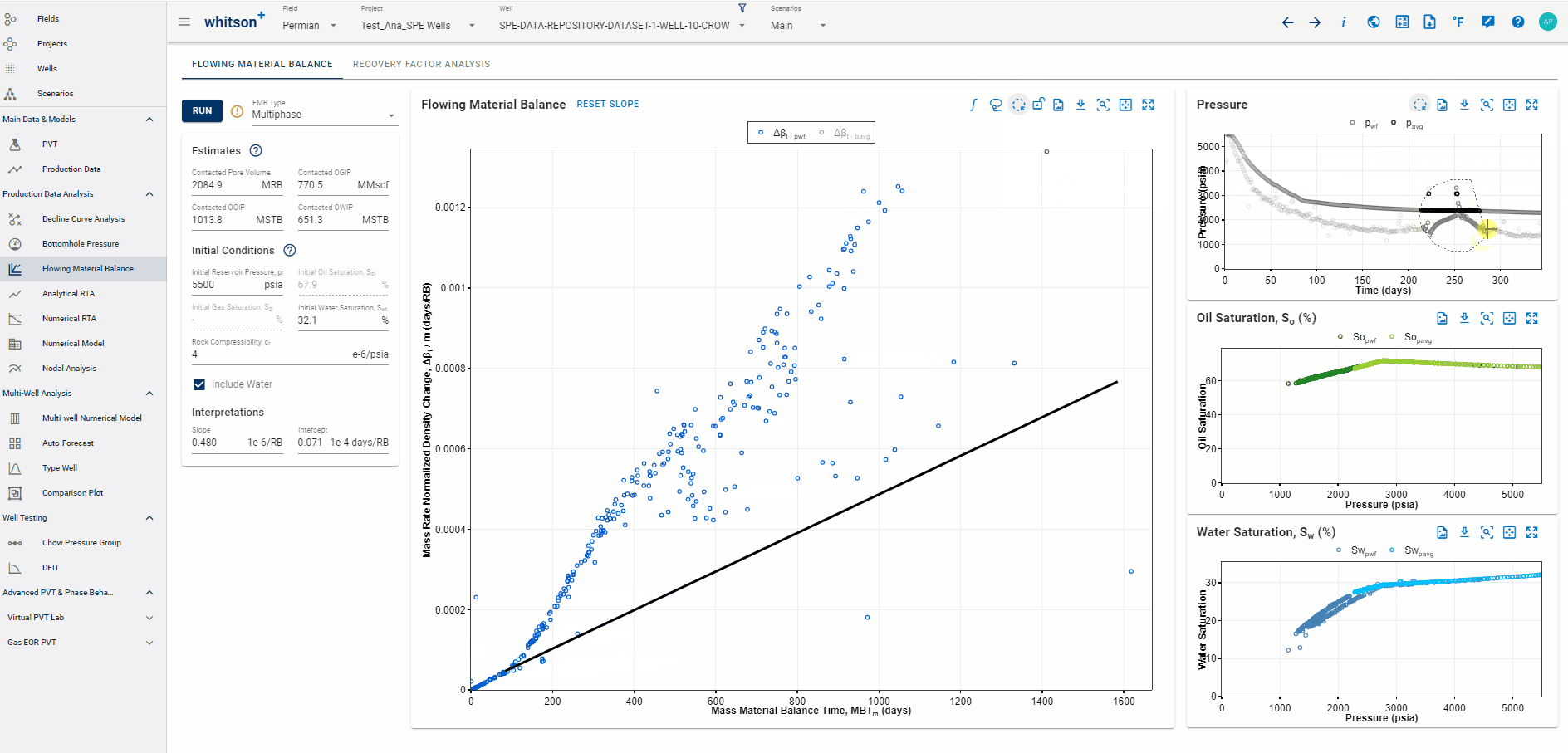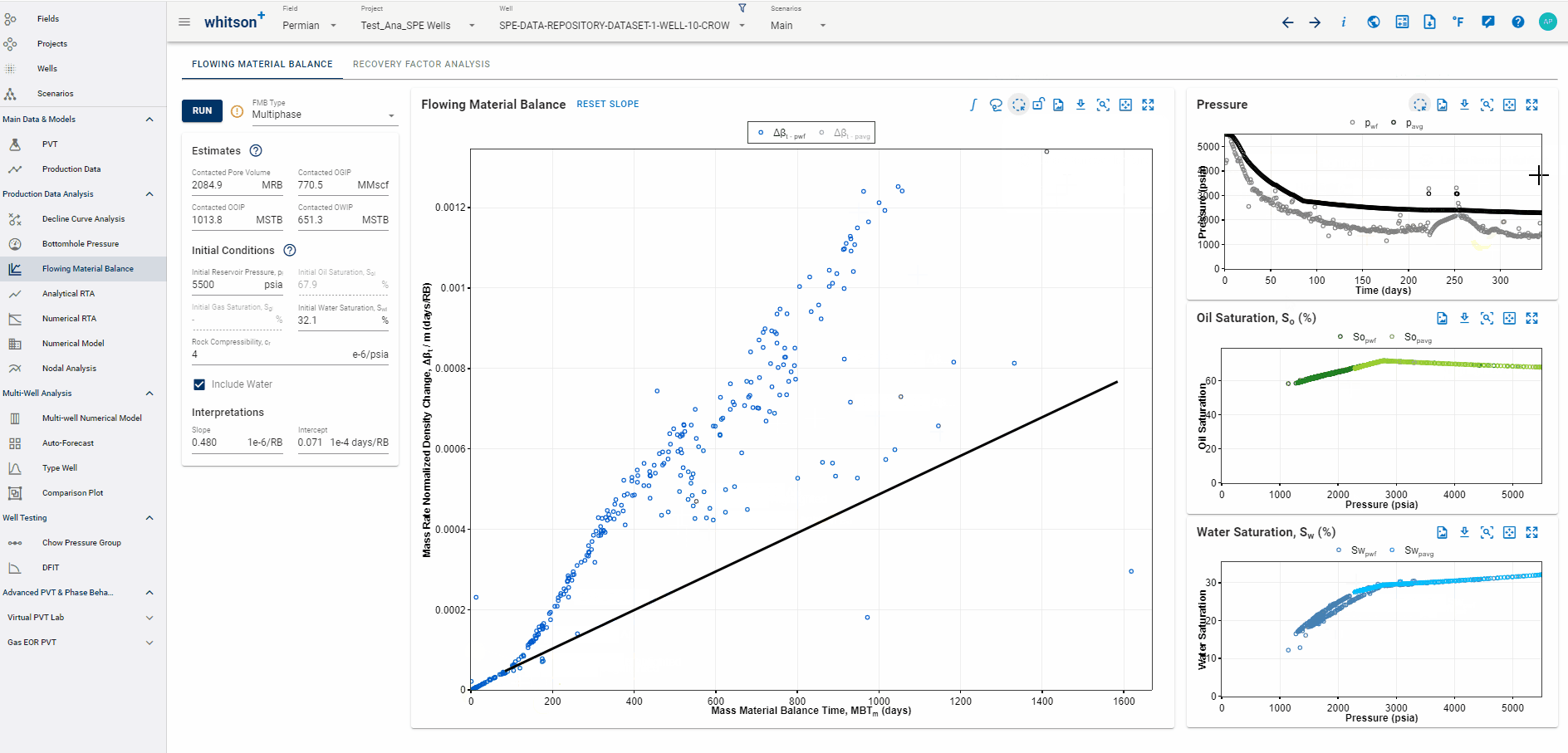
1.8 Highlighting data points across all plots
To highlight data across plots, click the "Lasso Highlight" icon in either the Flowing Material Balance or Pressure plot and select the desired data points. The selection will be highlighted in yellow across all plots for easy identification.
1.9 Autofit
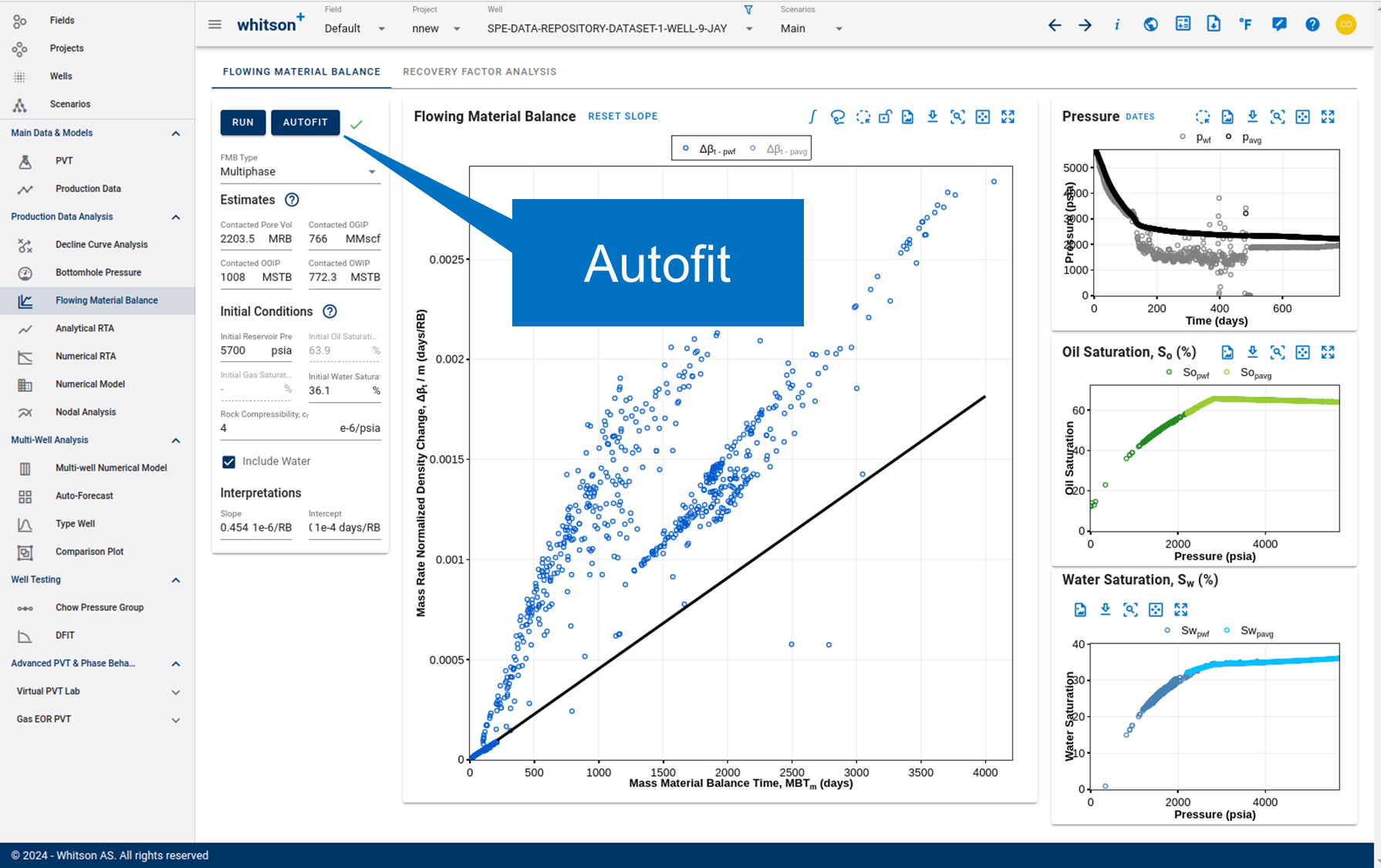
In multiphase Flowing Material Balance (FMB) analysis, the autofit feature selects the shallowest of the following two slopes, which translates into the largest pore volume:
- The slope of the datapoints when the flowing bottomhole pressure is above the saturation pressure.
- The slope derived from the last 20% of the observed history datapoints.
While this provides a solid foundation for interpretation, remember that many factors should be considered when analyzing a multiphase FMB plot.
2. Multiphase FMB: Theory
2.1 Governing Equation
Multiphase FMB equation is written as:
2.2 MFMB Integral
The multiphase FMB plot can be rather noisy when working with real data. An effective way to smooth the data is to calculate, and plot, the MFMB integral.
Let the left side of the governing equation be abbreivated
Let mass material balance time
The multiphase FMB integral is multiplied with 2 to ensure that the slope on the diagnostic plot still yields the contacted pore volume. This follows from
3. Multiphase FMB: Detailed Theory
This module is designed based on the workflow proposed by Thompson and Ruddick in URTeC 2022.
The workflow accounts for any phase and saturation changes during multiphase flow that are not accounted for using single phase flowing material balance techniques. Unlike other multiphase flowing material balance methods, no prior knowledge of relative permeability relationships or pseudopressure functions are required. It is based on mass material balance and requires production and PVT data only to determine original hydrocarbons-in-place (OHIP).
Classic single-phase FMB combines pseudo-steady-state flow theory with material balance. This workflow relies on the same assumption that during constant-rate pseudo-steady-state flow the mixture density at all locations in the reservoir declines at the same rate.
Why doesn't the multiphase FMB method require inputted pressure dependent permeability (if relevant)?
"All transport dependent terms (permeability, relative permeability, etc.) are built in to the rates. They never appear explicitly."
Leslie Thompson
Multiphase FMB equation is written as:
where \(\beta\) is defined as mixture density (lbm/bbl),
\(\gamma\) is the ratio of the pore volume to the initial pore volume at the pressure of interest
\(c_r\left(p\right)\) is the rock compressibility as a function of pressure. \(\dot{m}\) is the total mass production rate (lbm/d), defined as
\(MBT_M\) indicates mass material balance time (day),
with \(M_T(t)\) represents the total cumulative mass of oil, gas and water produced from the reservoir (lbm),
in which subscript \(i\) and overbar reflect initial and average reservoir condition, respectively. Subscript \(o\), \(g\) and \(w\) represent oil, gas and water properties. \(\rho_{sc}\) is density at standard condition (lbm/scf), \(S\) is saturation, \(B\) is formation volume factor and \(q\) is fluid production rate. The other variables are \(V_p\) for pore volume (RB), \(N_p\), \(G_p\) and \(W_p\) are oil, gas and water production.
According to Eq. \eqref{eq:multiphase-FMB}, plot of mass rate normalized density difference \(\left(\frac{\beta_i-\bar{\beta}}{\dot{m}(t)}\right)\) versus mass material balance time \(\left({MBT}_M\right)\) will result in a straight line with slope equal to inverse of the pore volume \(\left(\frac{1}{V_p}\right)\). The constant \(\frac{1}{b_M}\) results because there is a delay in the time at which boundary dominated flow occurs at the wellbore.
From this pore volume, one can simply calculate OHIP by using the following relationships:
The component concentrations of oil, gas and water (\(\zeta_o\), \(\zeta_g\) and \(\zeta_w\)) are defined
If we consider net mass conservation on the reservoir volume directly adjacent to the producing wellbore, we can state that:
- At early times, the reservoir and near-wellbore cumulative producing fluid ratios are identical since all production comes from the near-wellbore region.
- At later times, the reservoir and near-wellbore cumulative producing fluid ratios are approximately equal.
Then we can derive the following cumulative production ratio relationships:
\(OGR\) and \(WGR\) are cumulative producing oil-gas ratio in STB/Mscf and cumulative producing water-gas ratio in STB/Mscf, respectively. Rearranging Eqs. \eqref{eq:Oil-Gas-Ratio} and \eqref{eq:Water-Gas-Ratio}, we can solve for saturations.
where
Total compressibility accounts for the compressibility of the fluid phases present in the system as well as the rock compressibility and is written as
where \(c_g\), \(c_o\), \(c_w\) and \(c_r\) denote gas, oil, water and formation (rock) compressibility, respectively. The default value of \(c_r\) is 4x10\(^{-6}\) 1/psia and \(c_w\) is 2.8x10\(^{-6}\) 1/psia in whitson+.
The author's complete derivation can be seen here. For further information on the derivation, please refer to URTeC-3718045 by Thompson and Ruddick.
3.1 Intercept on the multiphase FMB Plot
It is physically impossible to have a negative intercept in the MPFMB. Under normal depletion that should never happen.
The theoretical minimum intercept if the reservoir is behaving like a perfect tank is zero (0). The average pressure line is the theoretical lowest line for the plot.
If the wellbore data falls below that it can only be because of pressure support from somewhere else (e.g. a bash).
For positive intercepts, the recovery factor calculations are fairly insensitive to the intercept value, but one should see slightly lower recovery factors as the intercept gets larger.
3.2 Note on a slightly compressible fluid by Leslie Thompson
For a slightly compressible fluid with small constant compressibility producing at constant rate during pseudosteady state flow we can show that
For these fluids, we can also show that the density at any pressure is
Where c is the compressibility, and sc means standard conditions. It is clear that
So for these systems, saying that \eqref{eq:dpdt} is equivalent to saying that
Also, for these systems, we accept that rate normalized pressure drop is a linear function of material balance time during boundary dominated flow. Again, I can easily argue that for this system this is equivalent to saying that mass rate normalized density change will be a linear function of mass material balance time due to the simple relationship between density and pressure.
Multiphase depletion is extremely complicated, with local depletion depending on pressure and local compositions (which are continuously changing at different points in the reservoir). It is therefore extremely surprising that a simple 1-cell tank model can capture enough of the depletion physics of a reservoir to enable us to use the classical (Schilthius) material balance equation on our reservoir production data. Nevertheless, we accept without question that this classical method works, and has historically been shown to work versus simulated data. The method we propose is similar. It cannot capture the extremely complex local reservoir behavior at every point, but it captures enough of the physics that it gives a very good approximation of what is happening globally in a reservoir.
4. Workflow
Multiphase FMB Workflow
- From provided PVT data, calculate initial properties (\(B_{oi}\), \(B_{gi}\), \(B_{wi}\), \(R_{si}\) and \(R_{vi}\)) then calculate initial mixture density \(\beta_{ti}\) using Eq. \eqref{eq:Mixture-Density}.
- From the production data, calculate the following properties for every time step:
- Cumulative production (\(N_p(t)\), \(G_p(t)\) and \(W_p(t)\))
- Total mass production rate (\(\dot{m}(t)\)) using Eq. \eqref{eq:Total-Mass-Production}
- Total mass produced (\(M_T(t)\)) using Eq. \eqref{eq:Cumulative-Mass-Produced-Total}
- Mass material balance time (\(MBT_M(t)\)) using Eq. \eqref{eq:Mass-Material-Balance}
- Fluid properties (\(B_{o}(t)\), \(B_{g}(t)\), \(B_{w}(t)\), \(R_{s}(t)\) and \(R_{v}(t)\))
- Oil, water and gas saturation (\(S_o\), \(S_w\) and \(S_g\)) using Eqs. \eqref{eq:Oil-Saturation}, \eqref{eq:Water-Saturation} and \eqref{eq:Gas-Saturation}
- Mixture density (\(\beta (t)\)) using Eq. \eqref{eq:Mixture-Density}
- Mass rate normalized density difference \(\left(\frac{\Delta\beta}{\dot{m}(t)}=\frac{\beta_i-\beta(t)}{\dot{m}(t)}\right)\)
- Plot \(MBT_M\) vs. \(\frac{\Delta\beta}{\dot{m}(t)}\)
- Find slope and intercept. According to Eq. \eqref{eq:multiphase-FMB}, the inverse of slope is pore volume (\(V_p\)) in RB.
- Calculate original hydrocarbons-in-place (OHIP) using Eqs. \eqref{eq:OIP}, \eqref{eq:GIP} and \eqref{eq:WIP}.
5. Refracs
A ‘refrac’ or refracturing treatment refers to the process of performing another hydraulic fracturing operation on a well that has already undergone the process in the past.
This restimulation of a well by pumping high pressure fluid into the well to create new fractures or to restimulate existing ones that have become less productive over time after an initial period of production.
Ultimately, refracs can tap into unstimulated parts of the reservoir with higher pore pressure and is seen as an effective way to increase production and may be a cost-effective alternative to drilling new wells.
5.1 Refrac Analysis Workflows
There are two main reasons to do a Refrac Analysis –
-
If you want to evaluate an already existing refrac, we recommend the paper below (Young et. al., 2023) where we analyzed 46 Refracs in Eagle Ford using whitson+. The workflow recommends the use of MFMB for this purpose, and is outlined in the subsequent section.
-
If you'd like to predict the uplift on a new refrac (that hasn't been done yet), check the section in Numerical Modeling here.
5.1.1 Existing Refrac Analysis Workflow
- Set initial reservoir conditions and initialize PVT, and calculate BHP.
- Use the MFMB plot to capture the late time and early time slope before and after the refrac.
- Compare the OOIP generated by the slope picks before and after the refrac at early time and late time separately and estimate the average increase in OOIP.
Fig. 6: Overall Refrac Evaluation Workflow.
If the refrac was successful, the MFMB method should resolve a higher contacted OOIP after the refrac compared to before in both early and late time slope picks.
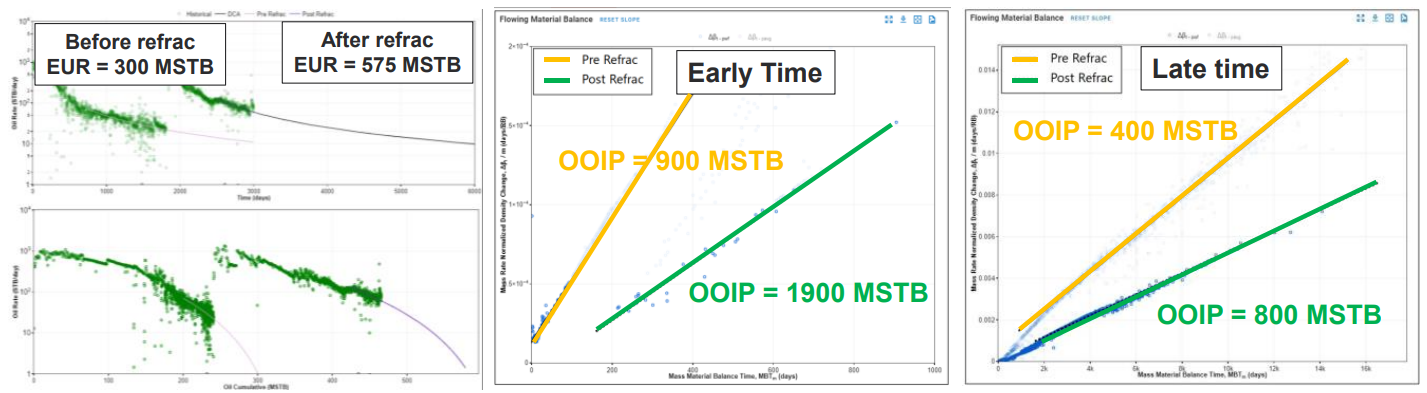
Fig. 7: Key plots related to a successful refrac in the Eagle Ford.
If the refrac was unsuccessful, you will see the same or smaller volume in both pre and post refrac slope picks.
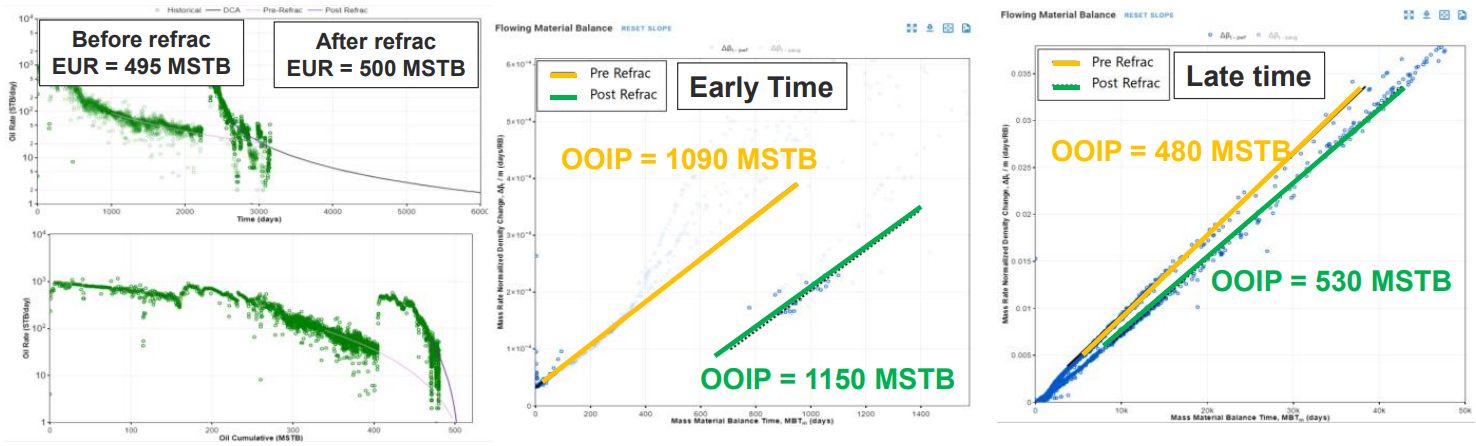
Fig. 8: Key plots related to an unsuccessful refrac in the Eagle Ford.
If you need any assistance in replicating this workflow or have any questions at all, contact us or use the Send Feedback button at the top right of whitson+ anytime.
This is summarized in this slide deck →→here←←.