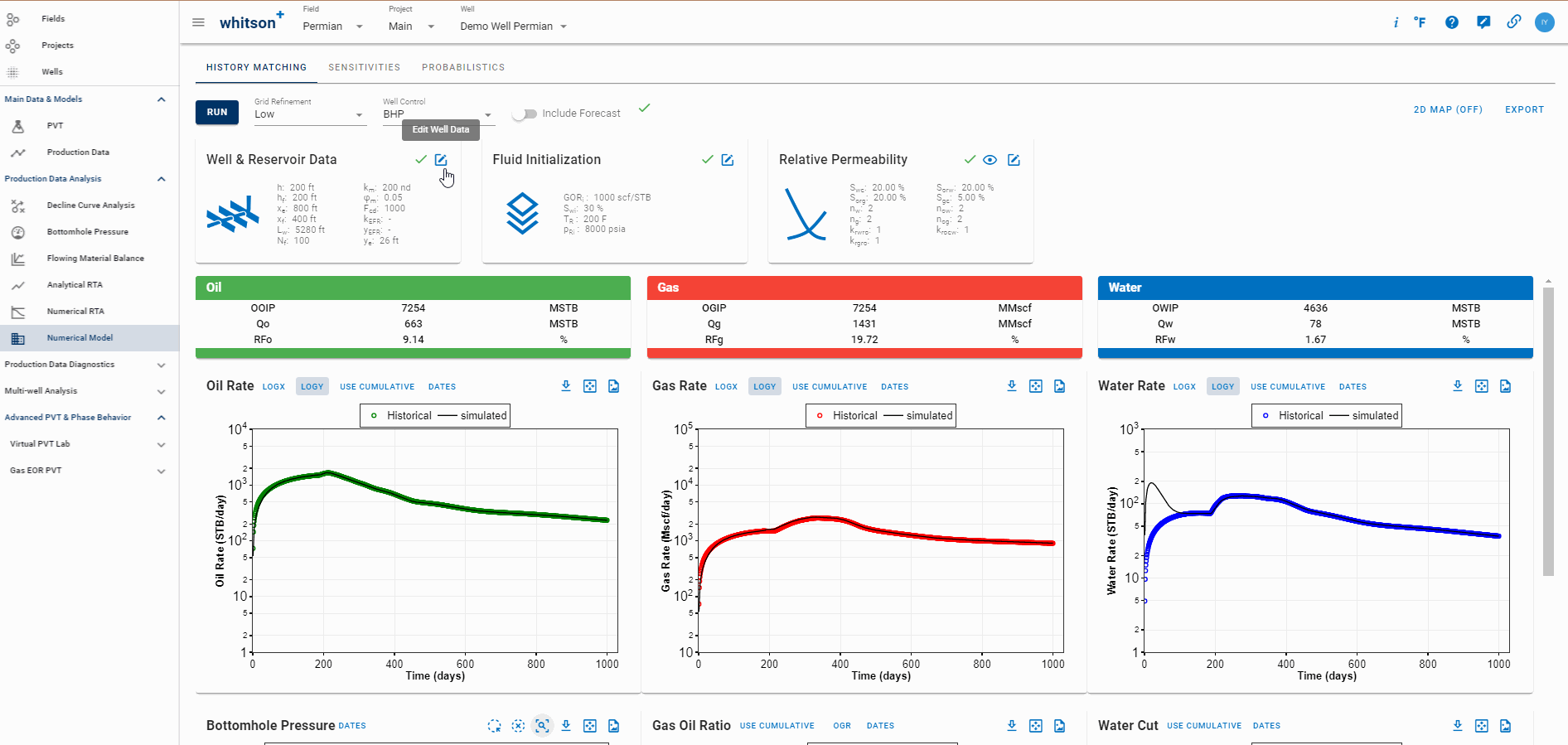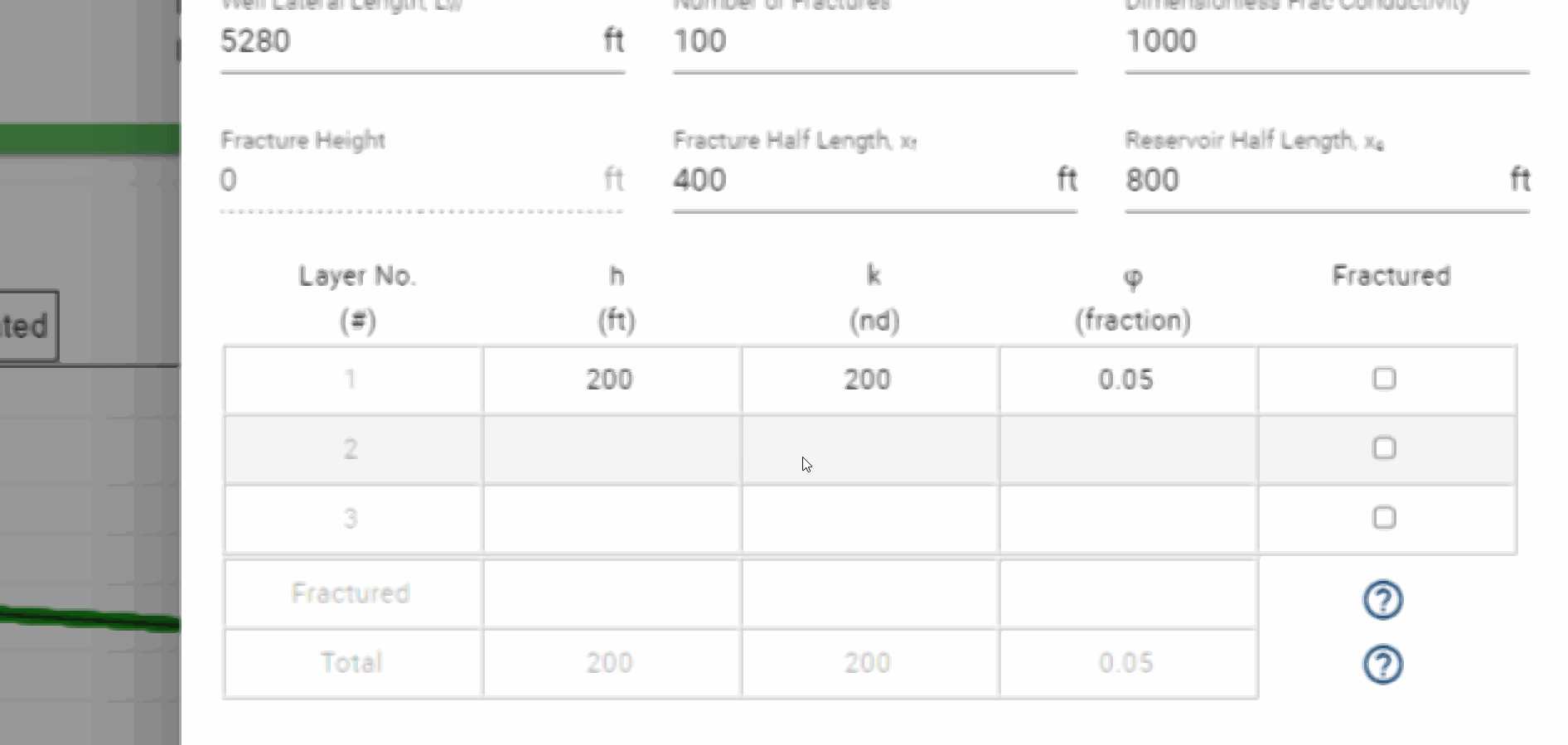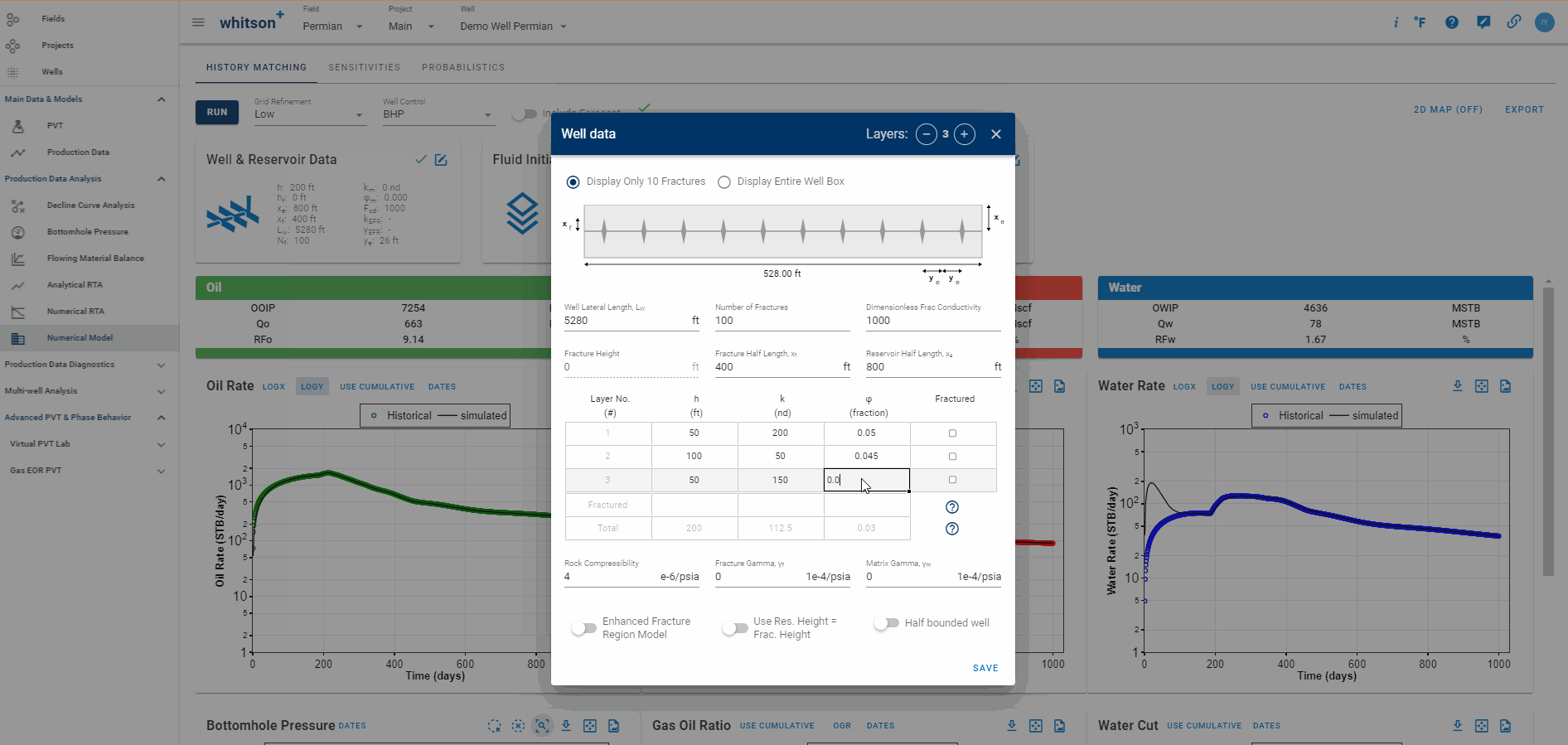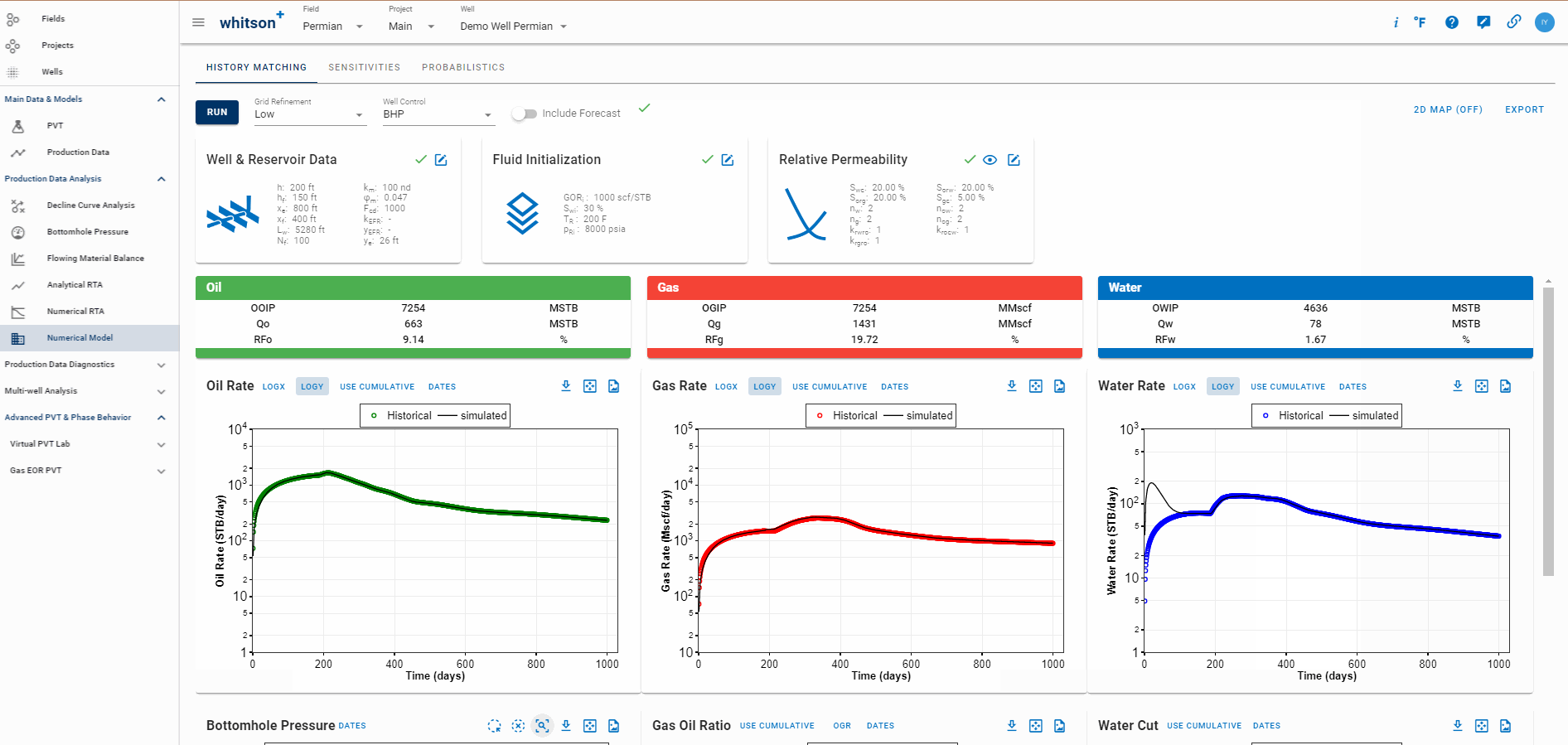
History Matching

The reservoir simulation module is designed to model depletion performance in tight unconventionals. The OPM Flow reservoir simulator, an open-source simulator using Eclipse 100 input syntax, is the engine of the tool.

1. Theory

1.1 Wellbox Model

The simulations are performed on a prebuilt model that represents the typical well in tight unconventionals, often referred to as a multi-fractured horizontal well (MFHW). The prebuilt model is called the wellbox model. A cartoon of the wellbox model is shown in Fig. 1.

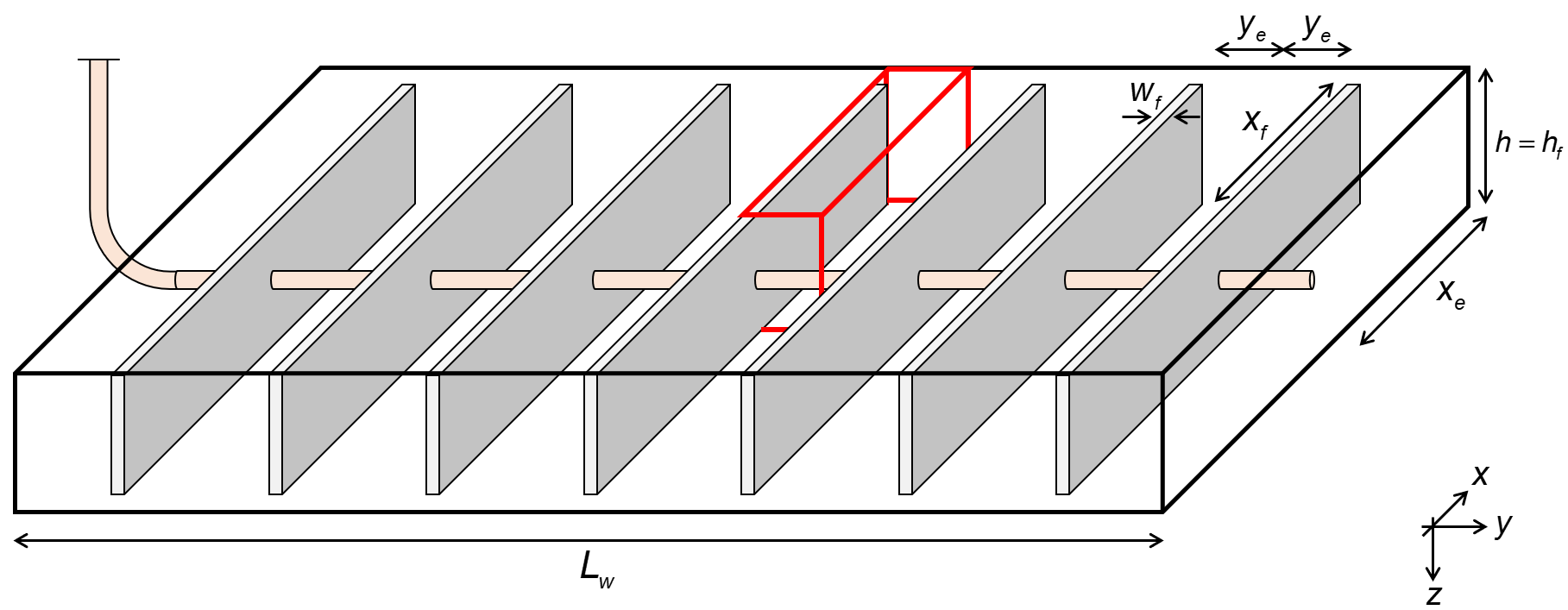
Fig. 1: Wellbox model

The wellbox model will have dimensions that the user can change, but a set of default values will be given initially. The dimensions and default values are as follows:

Dimension	Symbol	Default Value
Lateral Length	\(L_w\)	5280 ft
Reservoir Half-Extent	\(x_e\)	800 ft
No. of Fractures	\(N_f\)	100
Fracture Half-Length	\(x_f\)	400 ft
Reservoir and Fracture Height	\(h_f\)	150 ft

As the wellbox model is symmetric, the numerical model will be a one-quarter fracture, as highlighted by a red-lined box in Fig. 1. The production from the numerical model is upscaled to by using a scaling factor. The scaling factor is defined as

$$\begin{equation} M = 4N_f \label{eq:scalingfactor} \end{equation}$$

where \(N_f\) is the number of hydraulic fractures (clusters) in the wellbox model. The dimensions of the numerical model are the same as the wellbox model, except for the y-dimension, where instead of \(L_w\), we use \(y_e\) defined as

$$\begin{equation} y_e = \frac{2L_w}{M} \label{eq:fracspachalf} \end{equation}$$

1.2 Enhanced Fracture Region (EFR) Option

It is possible to introduce a region of enhanced, effective permeability, \(k_{EFR}\), around each fracture with extent, \(y_{EFR}\). An example description for a single-fracture is illustrated in Fig. 2. The reservoir can extend beyond the fracture tip, and have contributions beyond the fracture height. The enhanced fracture region has the same height and length as the fracture, only difference being the extent in the y direction.

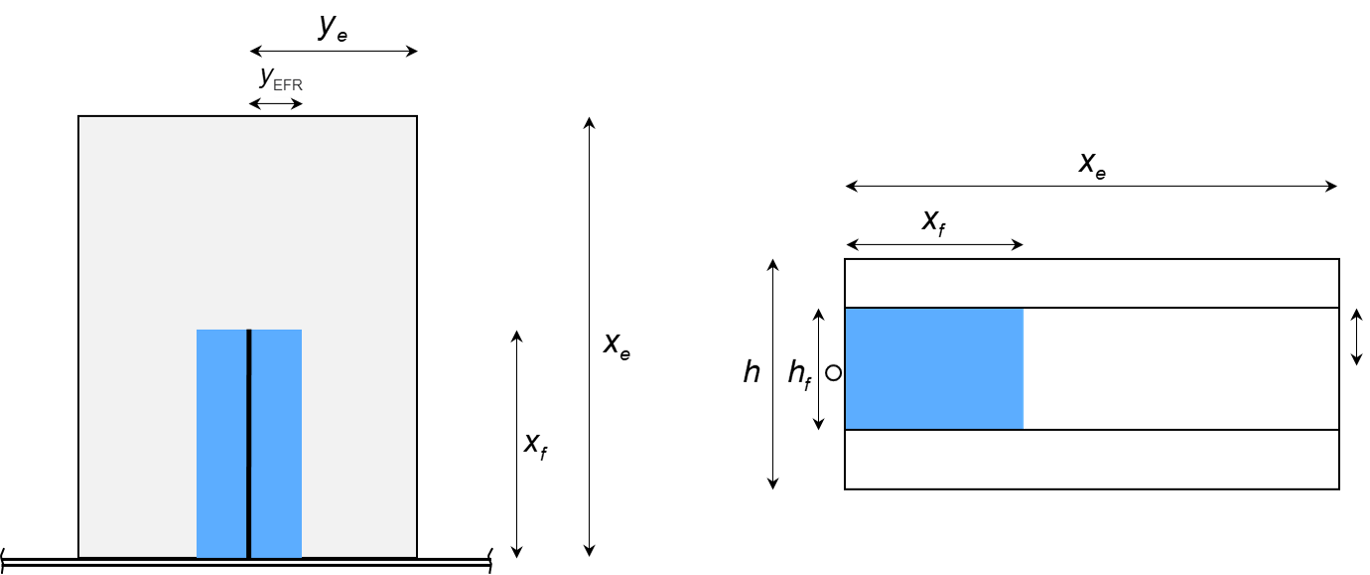
Fig. 2: Enhanced fracture region model

Pressure Dependent Permeability in the EFR region - Matrix gamma is applied to the EFR region, read more about pressure dependent permeability here.

EFR in whitson⁺

You can activate EFR in the model by toggling the EFR switch on in the 'Well and Reservoir Data' card. You will need to specify the extent of this EFR as a distance into the matrix from each fracture (less than the fracture spacing) for the enhanced permeability to be applied in this zone, as shown in the GIF below, where we add a 3ft EFR around the fracture with 10x matrix permeability:

When the EFR option is activated in whitson⁺, the LFP (A√k) reported in the Well & Reservoir Data card uses the EFR permeability (k_EFR) instead of the matrix permeability (k_m) to calculate.

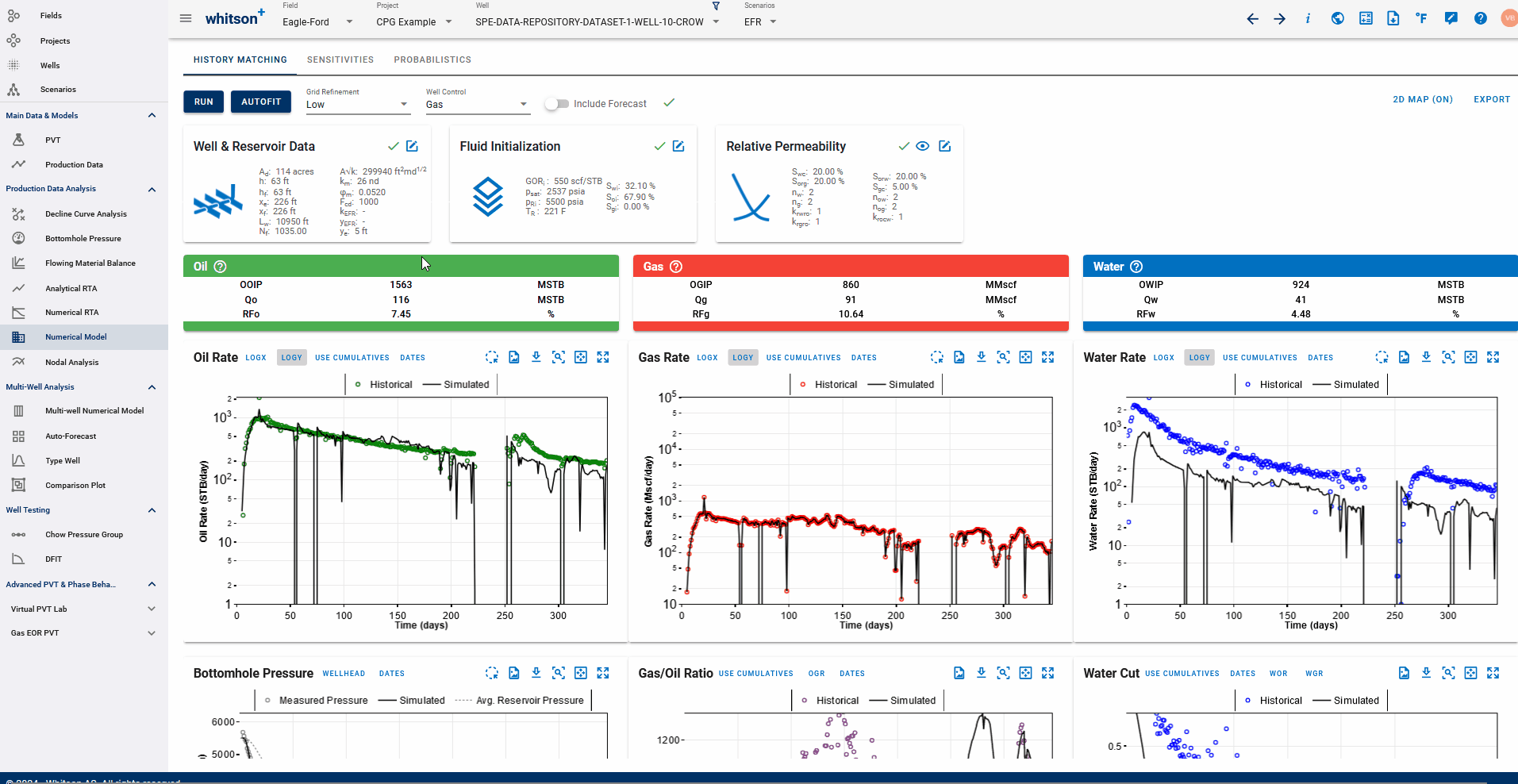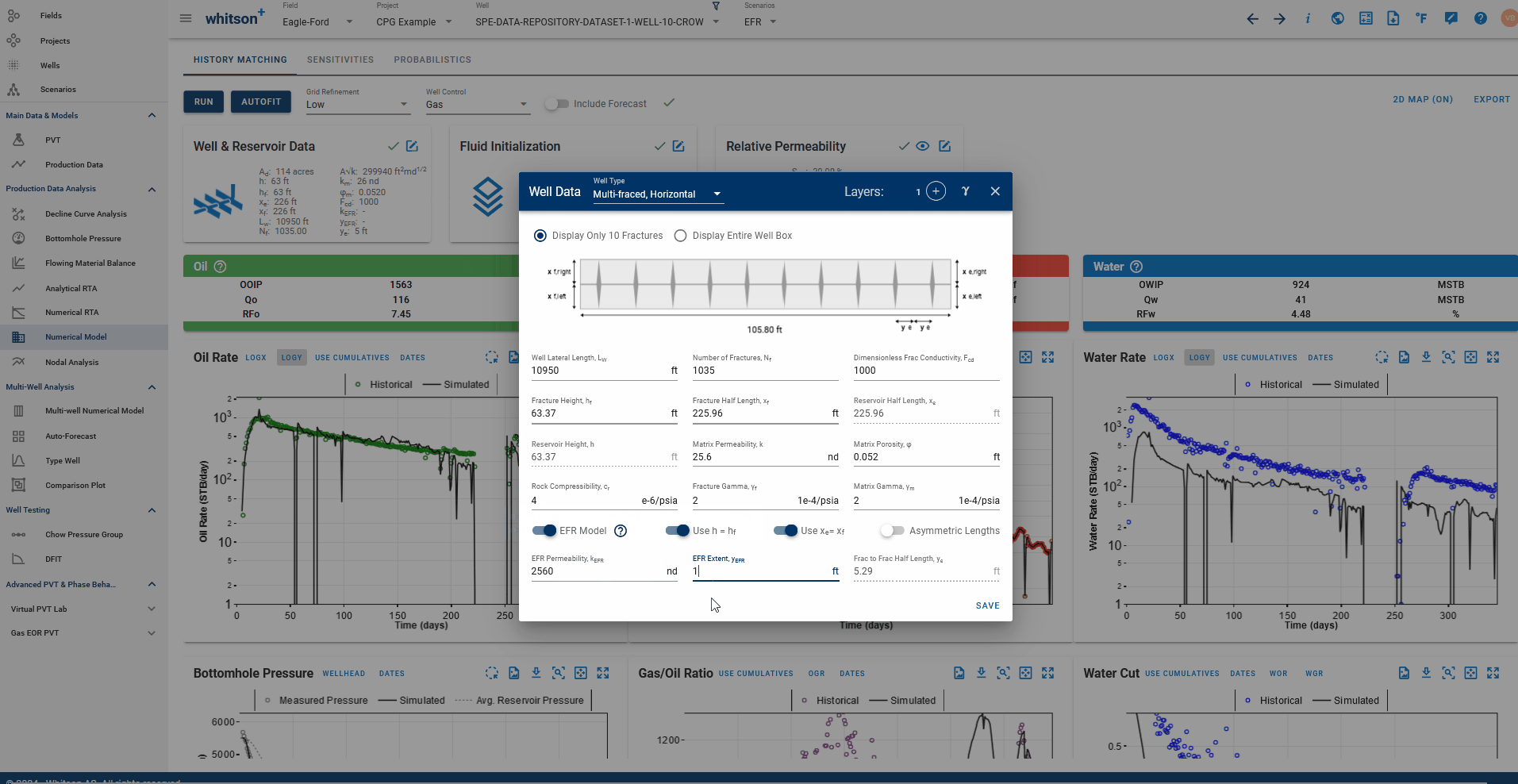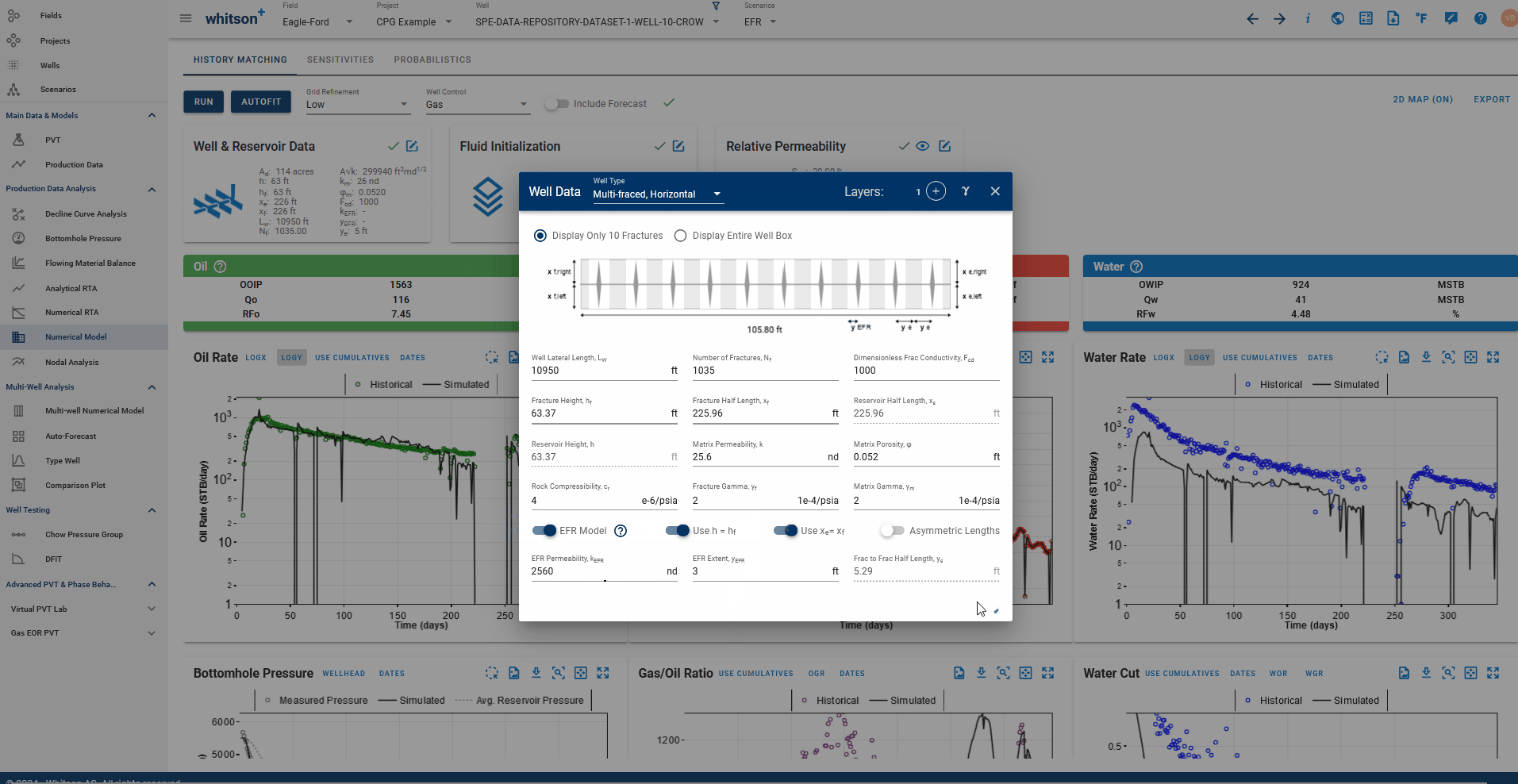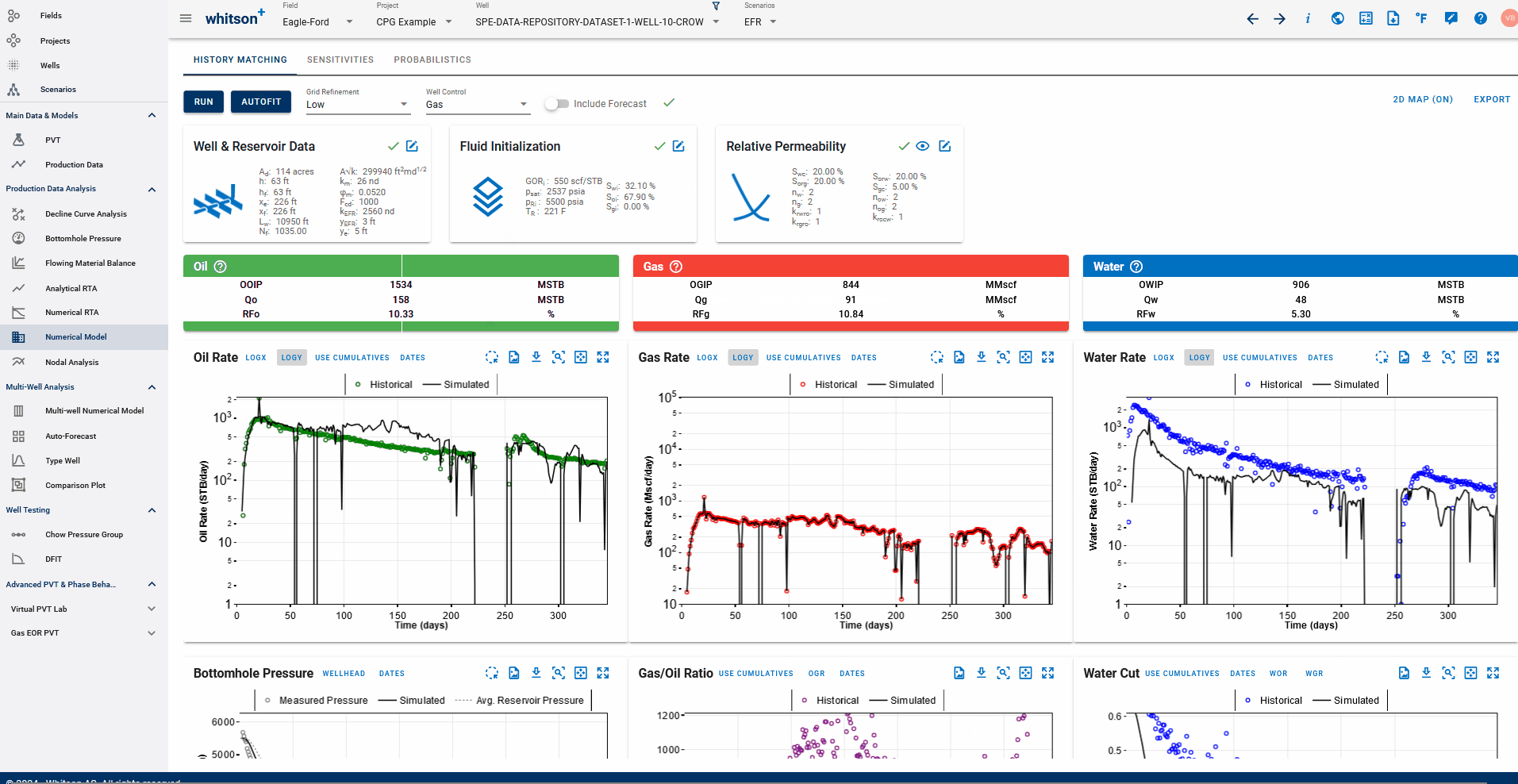
1.3 Reservoir Properties

1.3.1 Grid-Block Properties

The reservoir properties will include some properties that can be changed by the user, and some properties that are locked. The changeable reservoir properties are given the following table:

Property	Symbol	Default Value
Matrix Porosity	\(\phi_m\)	0.03
Matrix Permeability	\(k_m\)	100 nd
Matrix Initial HC Saturation (Fluid Dep.)	\(S_{HCi}\)	1
Matrix Initial Water Saturation	\(S_{wi}\)	\(S_{wc}\)
Initial Reservoir Pressure	\(p_{Ri}\)	7500 psia
Hydraulic-Fracture Dimensionless Conductivity	\(F_{CD}\)	100

The locked reservoir properties are as follows

Property	Symbol	Default Value
Fracture Porosity	\(\phi_f\)	0.1
Fracture Width	\(w_f\)	0.1 ft
Depth	\(D\)	10000 ft

Note that depth is merely a cosmetic property as there is only one horizontal layer in the model, and no tubing calculations are made.

The dimensionless fracture conductivity is defined as

$$\begin{equation} F_{CD} = \frac{w_f k_f}{x_f k_m} \label{eq:dimlessfraccond} \end{equation}$$

We calculate \(k_f\) from equation (3).

1.3.2 Saturation-Dependent Properties

1.3.2.1 Two-Phase Relative Permeability

The saturation-dependent properties in this model are the relative-permeability curves. We use the Corey-type model to express two-phase relative permeability. Baker's linear interpolation model is used to calculate \(k_{ro} = f(S_w,S_g)\) in three-phase systems.

The Corey-type model calculates \(k_{rw} = f(S_w), k_{row} = f(S_w)\), \(k_{rog} = f(S_g)\), and \(k_{rg} = f(S_g)\) as follows:

$$\begin{equation} k_{rw}(S_w) = k_{rwro}\bigg(\frac{S_w-S_{wc}}{1-S_{orw}-S_{wc}}\bigg)^{n_w} \label{eq:rpwat} \end{equation}$$

$$\begin{equation} k_{row}(S_w) = k_{rocw}\bigg(\frac{1-S_{orw}-S_{w}}{1-S_{orw}-S_{wc}}\bigg)^{n_{ow}} \label{eq:rpoilwat} \end{equation}$$

$$\begin{equation} k_{rog}(S_g) = k_{rocw}\bigg(\frac{1-S_{org}-S_{wc}-S_g}{1-S_{org}-S_{wc}}\bigg)^{n_{og}} \label{eq:rpoilgas} \end{equation}$$

$$\begin{equation} k_{rg}(S_g) = k_{rgro}\bigg(\frac{S_g-S_{gc}}{1-S_{org}-S_{wc}-S_{gc}}\bigg)^{n_{g}} \label{eq:rpgas} \end{equation}$$

where the following parameters must be provided

Property	Symbol	Default Value Matrix	Default Value Fracture
Connate Water Saturation	\(S_{wc}\)	0.2	0
Residual Oil Saturation (O-W)	\(S_{orw}\)	0.2	0
Residual Oil Saturation (O-G)	\(S_{org}\)	0.2	0
Critical Gas Saturation	\(S_{gc}\)	0.05	0
Water Corey Exponent	\(n_w\)	2	1
Oil Corey Exponent (O-W)	\(n_{ow}\)	2	1
Oil Corey Exponent (O-G)	\(n_{og}\)	2	1
Gas Corey Exponent	\(n_g\)	2	1
Water Relative Permeability at \(S_{orw}\)	\(k_{rwro}\)	1	1
Oil Relative Permeability at \(S_{wc}\)	\(k_{rocw}\)	1	1
Gas Relative Permeability at \(S_{org}\)	\(k_{rgro}\)	1	1

The relative-permeability values in the matrix will be open for change by the user. The fracture values are locked.

1.3.2.2 Three-Phase Relative Permeability

To achieve platform consistency between the different simulators (OPM Flow, Eclipse 100, Sensor, CMG IMEX), we have found that the Baker linear interpolation of \(k_{ro}\) is the only three-phase relative permeability that is common for all simulators.

The Baker linear interpolation correlation is as follows

$$\begin{equation} k_{ro}(S_w,S_g)=\frac{(S_w-S_{wc})k_{row}+S_gk_{rog}}{S_w-S_{wc}+S_g} \end{equation}$$

The testing of OPM Flow has been done by comparing OPM Flow to Sensor. The default three-phase relative permeability correlation in Sensor is Stone 1 with Fayer's and Matthew's expression for \(S_{om}\). This option is not available in OPM Flow, which results in inconsistencies in predicted results for the two simulators. The default relative permeability correlation for OPM Flow (and E100) is the Baker linear interpolation. This correlation can also be activated in Sensor, making the two simulators consistent. However, Stone 1 with Fayer's and Matthew's expression for \(S_{om}\) remains the preferred choice, which was also the case for Keith Coats (see quote below)

The default three-phase relative-permeability correlation for CMG IMEX is Stone 2. Hence, for consistency, our output files to CMG IMEX format will contain a keyword activating the Baker linear interpolation correlation.

The table below summarizes the three-phase correlations available in the different simulators.

Three-Phase Rel.Perm. Correlation	Sensor	OPM FLow	Eclipse 100	CMG IMEX
Stone 1		X	X	X
Stone 1 with Fayer's and Matthew's	X		X	X
Stone 2	X	X	X	X
Baker	X	X	X	X

Quote

"I would never use Baker kr. Stone 2 kr is pathological and Baker kr may be. To my knowledge Stone 1 – Fayers kr (sensor default) is the only kr logic free of pathology"

"Default kro is Stone 1 with Fayer’s modification. The ID option STONE 2 can be pathological, depending upon entered water-oil and gas-oil krow and krog relperm data. The pathology is a step-function change from kro>0 to kro=0 for an epsilon change in saturations. The default Stone 1 is not pathological"

*Default refers to Sensor

Keith Coats

1.3.2.3 Relative Permeability and Producing Ratios

Understanding how relative permeabilities affect Gas-Oil Ratio (GOR) and Water-Oil Ratio (WOR), or water cut, can be tricky. It often takes experience, with engineers having their preferred parameters to tweak for achieving specific changes in simulated GOR, WOR, or other ratios. To simplify this, especially for beginners, we've created cheat sheets to help out.

GOR and \(S_{org}\)

To understand the relationship between GOR and \(S_{org}\), it is necessary to take a look at the equation for producing GOR:

$$\begin{equation} R_p=[1+ \alpha r_s]^{-1}[R_s+ \alpha] \end{equation}$$

$$\begin{equation} \alpha=\frac{k_{rg}B_o \mu_o}{k_{ro}B_{gd} \mu_g} \end{equation}$$

Just to simplify things slightly, it can assume that \(r_s\) is 0

$$\begin{equation} R_p=\frac{q_w}{q_{\bar{o}g}+q_{\bar{o}o}}=R_s+\frac{k_{rg}B_o \mu_o}{k_{ro}B_{gd} \mu_g} \end{equation}$$

The producing GOR is a combination of PVT properties and relative mobilities (\(k_{rg}\)/\(k_{ro}\)).

Reducing the \(S_{org}\), will reduce \(k_{rg}\)/\(k_{ro}\) (example below), and hence reduce producing GOR.

However, the relative reduction in \(k_{rg}\)/\(k_{ro}\) (and hence relative GOR reduction) will be a function of what the \(S_g\) is.

\(S_g\) is a function of fluid type (i.e. less gas comes out of solution of a low GOR oil with \(R_{si}\) = 500 scf/STB vs a near-critical fluid with \(R_{si}\) = 3500 scf/STB).

For the example below-

• If e.g. \(S_g\) is 50% (i.e. a more gassy fluid), the difference by changing \(S_{org}\) down to 0% would mean a reduction in \(k_{rg}\)/\(k_{ro}\) from 24 down to 2.5 (example). Order of magnitude difference.

• If e.g. \(S_g\) is 10% (i.e. a less gassy fluid), the difference by changing \(S_{org}\) down to 0% would mean a reduction in \(k_{rg}\)/\(k_{ro}\) from 0.01xx to 0.01yy (example). Almost no difference.

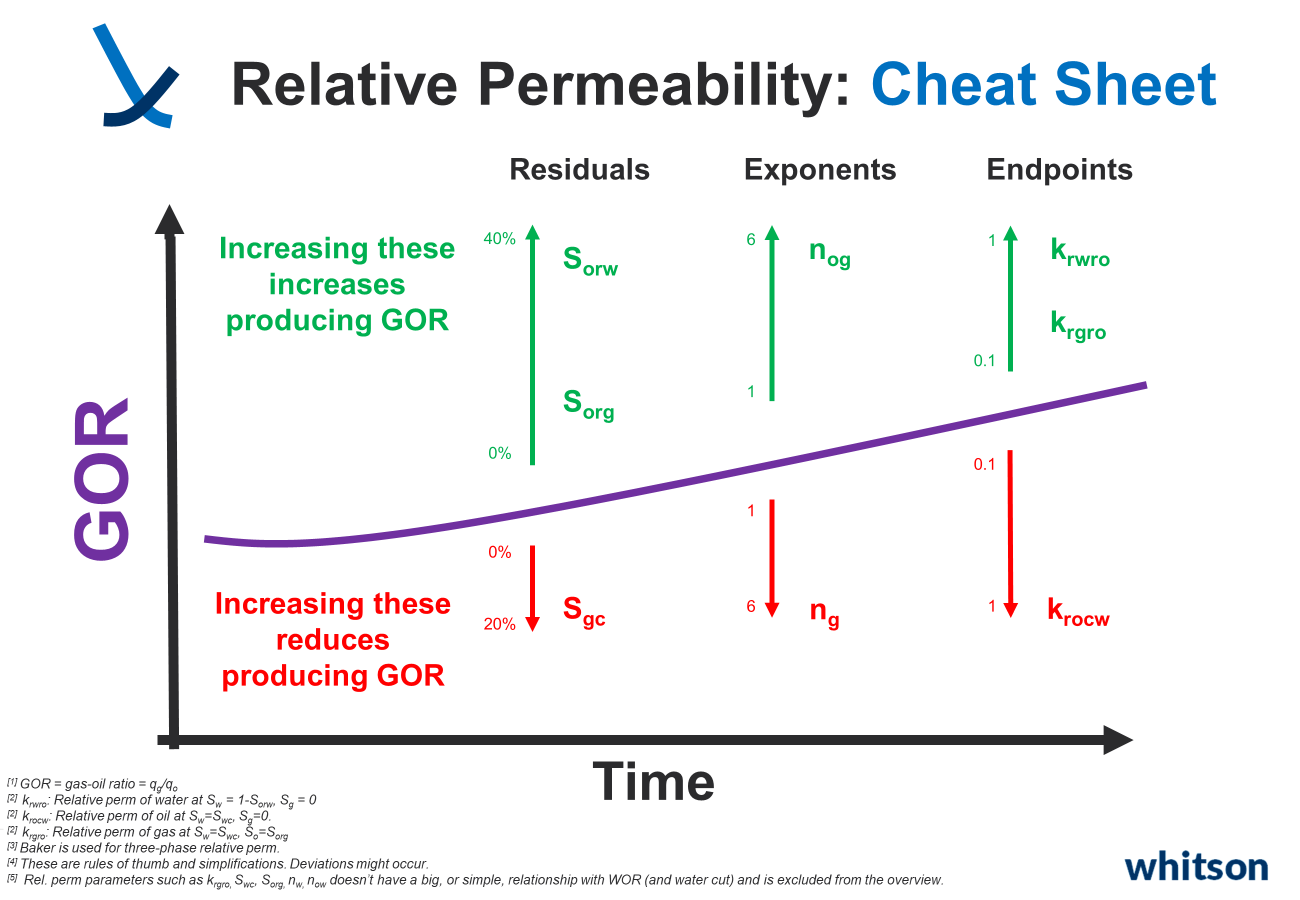
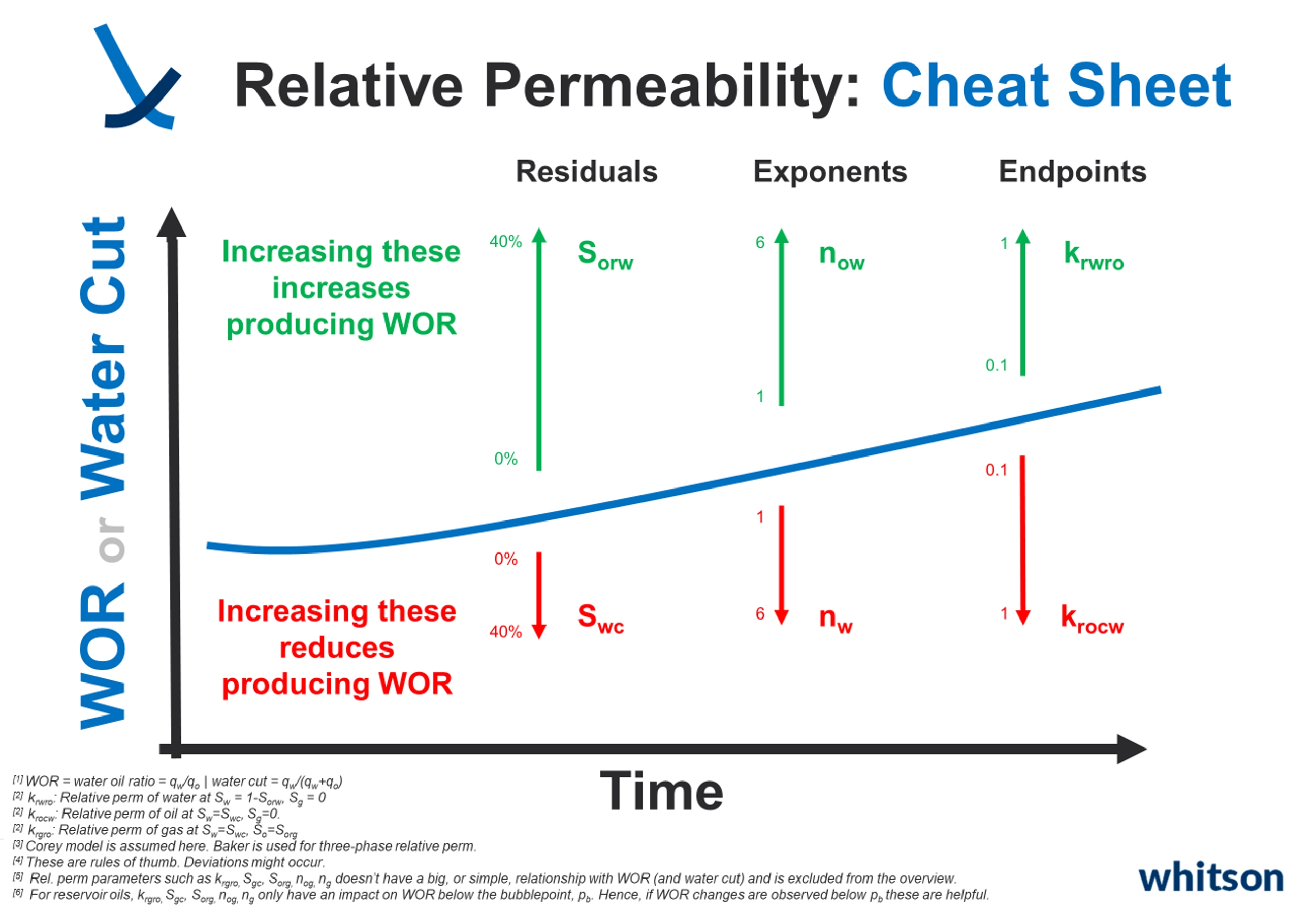
Relative Permeability in whitson⁺

Here's how you can adjust the relative permeability for your numerical model and visualize the rel-perm curves set up from these settings. Be sure to run the numerical model after editing the relative permeability table for the updated curves to be databased and displayed.

1.3.3 Multi-Layer Models

In whitson+, it is possible to have more than single layer in the model with fully or partially penetrating fracture.

The fractured layer properties are calculated by height weighted average of the \(n\) penetrated layers, as follows

$$\begin{equation} \label{eq:hf} h_f=\sum_{i=1}^{n}h_i \end{equation}$$

$$\begin{equation} \label{eq:kf} k_f=\frac{\sum_{i=1}^{n}h_ik_i}{\sum_{i=1}^{n}h_i} \end{equation}$$

$$\begin{equation} \label{eq:phif} \phi_f=\frac{\sum_{i=1}^{n}h_i\phi_i}{\sum_{i=1}^{n}h_i} \end{equation}$$

Multi-layer model, multi-fluid initialization in whitson⁺

You can not only set up a multi-layer model as outlined above, but you can also initialize PVT for each layer independently. You can set up each layer with its own fluid composition and black oil tables, that will be used to simulate phase mobility in each layer separately. Typical uses may include modeling water breakthrough as layers with 100% water saturation, etc. The steps to create multi-layer, multi-fluid models are outlined in the GIF below, where we add 2 additional layers and set up PVT such that there is only gas contribution from the layer on top and water contribution from the bottom layer:

1.4 Fluid Properties

whitsonʳˢ is designed to do simple and fast reservoir modeling to evaluate depletion performance. To make this tool as efficient as possible, the modified black-oil PVT model (outlined below) is used for the fluid treatment. An important feature of whitsonʳˢ is the direct link to whitsonᴾⱽᵀ. This makes the generation of black-oil PVT tables a backend feature in whitsonʳˢ, where the user only needs to provide key properties related to fluid PVT such as temperature, surface-process information (separator pressure and temperature), and initial gas/oil ratio.

The key parameters of the modified black-oil PVT model are (details and definitions are found in Whitson and Brulé 2000) as follows:

Property	Symbol
Oil Formation Volume Factor	\(B_{o}\)
Solution Gas/Oil Ratio	\(R_s\)
Dry-Gas Formation Volume Factor	\(B_{gd}\)
Solution Oil/Gas Ratio	\(r_s\)
Oil Viscosity	\(\mu_o\)
Gas Viscosity	\(\mu_g\)

whitsonʳˢ will return the in-place volumes of the wellbox model when all model dimensions, reservoir properties, and fluid properties have been specified. The in-place numbers are calculated as

$$\begin{equation} \text{IOIP}=x_ey_eh\bigg(\frac{S_{oi}}{B_{oi}}+\frac{S_{gi}r_{si}}{B_{gdi}}\bigg)M \label{eq:OOIP} \end{equation}$$

$$\begin{equation} \text{IGIP}=x_ey_eh\bigg(\frac{S_{gi}}{B_{gdi}}+\frac{S_{oi}R_{si}}{B_{oi}}\bigg)M \label{eq:IGIP} \end{equation}$$

$$\begin{equation} \text{IWIP}=x_ey_ehS_{wi}M \label{eq:IWIP} \end{equation}$$

1.5 Water and Rock Properties

The following water and rock properties are used as default values for all reservoir simulators.

Property	Symbol	Default Value
Water Formation Volume Factor at \(p_{ref}\) & \(T_R\)	\(B_w\)	1 RB/STB
Water compressibility	\(c_w\)	3x10\(^{-6}\) 1/psia
Surface water density	\(\rho_w\)	62.37 lb/ft\(^3\)
Water viscosity	\(\mu_w\)	0.5 cp
Reference pressure for \(B_w\)	\(p_{ref}\)	14.696 psia
Formation (rock) compressibility	\(c_r\)	4x10\(^{-6}\) 1/psia

1.6 Geomechanical Effects - Pressure-Dependent Permeability

The matrix, EFR (if activated), and hydraulic fracture can be assigned a pressure-dependent permeability on the form $$\begin{equation} k(p)=k(p_{Ri})\exp(\gamma(p-{p_{Ri}})) \end{equation}$$ where \(\gamma\) is a property that be assigned in the frontend. There are two different gamma values, on for the hydraulic fracture \(\gamma_f\), and one for the matrix and EFR (if activated) \(\gamma_r\). To activate the pressure-dependent permeability, toggle on "Pressure-Dependent Permeability" under the "Well & Reservoir Data" card in the "History Matching" module.

Pressure-Dependent Permeability in whitson⁺

Pressure dependent permeability can be added as a gamma value to the matrix and EFR(\(\gamma_r\)), and the fracture(\(\gamma_f\)) by bulk editing multiple wells (Well Overview page), directly in the well headers (Scenarios page), or by using input fields in NRTA and Numerical Model features - your changes to \(\gamma\) in any one of these places should be reflected in all other places.

You can visually set it up in the numerical model by specifying only the gamma to be used in the exponential relationship above to calculate and display the plot of permeability as a function of pressure. If you have tabulated data for the formation permeability at different pressures, you can also use the table directly to set up an interpolation for the permeability as a function of pressure.

You can include pressure dependent permeability as outlined in the GIF below:

1.7 Computing Original Gas in Place with Adsorption

Shale reservoirs possess a remarkable capacity to store methane through a process known as "adsorption." This involves gas molecules adhering to the organic material within the shale, creating a near-liquid state of condensed gas. A useful analogy is to envision a magnet sticking to a metal surface or lint clinging to a sweater, illustrating the concept of adsorption versus absorption, where one substance is trapped inside another like a sponge soaking up water. The adsorption process is reversible due to its reliance on weak attraction forces.

Compared to conventional reservoirs, shale reservoirs can store significantly more gas in the adsorbed state, even when compression is applied at pressures below 1000 psia. Notably, the gas stored in shale is predominantly held in the adsorbed state, as opposed to being free gas. This is because the volume of the cleat or fracture system within shale is relatively small compared to the overall reservoir volume. As a result, the pressure volume relationship is commonly described through the desorption isotherm alone.

Langmuir Isotherm

The release of adsorbed gas is commonly described by a pressure relationship called the Langmuir isotherm. The Langmuir adsorption isotherm assumes that the gas attaches to the surface of the shale, and covers the surface as a single layer of gas (a monolayer). At low pressures, this dense state allows greater volumes to be stored by sorption than is possible by compression.

The typical formulation of the Langmuir isotherm is:

$$\begin{equation} \label{eq:langmuir} c_g = \frac{V_{LS}p}{p_{LS}+p} \end{equation}$$

Langmuir Volume, V_LS

The Langmuir volume is the maximum amount of gas that can be adsorbed by a shale at a "infinite pressure". The plot below of a Langmuir isotherm demonstrates that gas content asymptotically approaches the Langmuir volume as pressure increases to infinity.

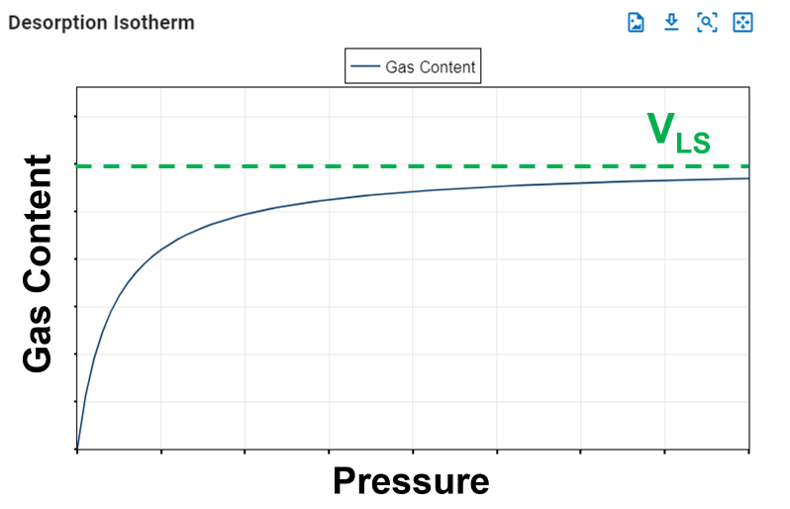
Fig. 1: Langmuir Volume

Langmuir Pressure, p_LS

The Langmuir pressure, or critical desorption pressure, is the pressure at which one half of the Langmuir volume can be adsorbed. As seen in the figure below, it changes the curvature of the line and thus affects the shape of the isotherm.

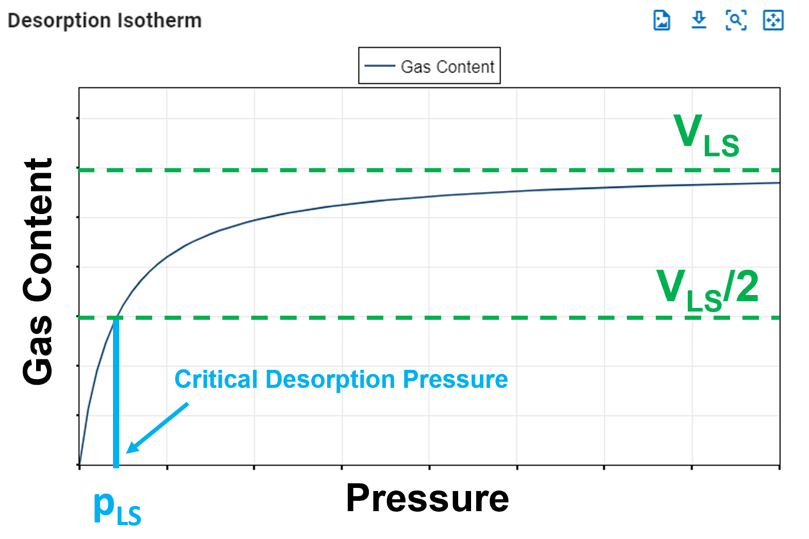
Fig. 2: Langmuir Pressure

Computing Original Gas in Place (OGIP)

Ambrose et al.[1] argue that the free (OGIP) must be corrected for the adsorbed gas that occupies some of the hydrocarbon pore volume (HCPV). If porosity is estimated from core plugs where core preparation has removed the adsorbed gas, then the OGIP will be overestimated.

The convention of reporting OGIP when adsorption is included, is to report it in units of scf/ton (standard cubic feet per short ton). For a fluid system having only dry/wet gas and water, the total OGIP is

$$\begin{equation} \hat{G}=\hat{G}_{f} + \hat{G}_a \end{equation}$$ where

$$\begin{align} \label{eq:freegasperton} \hat{G}_f &= C_1 \frac{\phi(1-S_{wi})-\phi_a}{\rho_bB_{gd}}\\ \label{eq:adsorbedgasperton} \hat{G}_a &= V_{SL} \frac{p}{p+p_{SL}} \end{align}$$ and $$\begin{equation} \phi_a = C_2 M_g \frac{\rho_b}{\rho_s}\bigg(V_{LS}\frac{p}{p+p_{LS}}\bigg) \end{equation}$$ with \(C_1\approx 5.7060\) and \(C_2\approx1.318\cdot10^{-6}\) are unit conversion factors. The shale saturation is capped at \(1-S_{wi}\), meaning the maximum amount of shale you can have is the entire HCPV. Hence, this will make the results independent of the adsorption numbers when violating this constraint.

The OGIP resolved in the ARTA and GFMB features yields the free OGIP. We can use this volume to compute the rock mass, which in turn can be used to calculate the adsorbed OGIP. Multiplying equation \eqref{eq:freegasperton} with the rock mass (\(G=\hat{G}_f m_r\)) gives the free OGIP in units of scf. Solving for the rock mass yields

$$\begin{equation} m_r = \frac{G_f}{C_1} \frac{\rho_b B_{gd}}{\phi(1-S_w)-\phi_a} \end{equation}$$

This rock mass can then be multiplied by equation \eqref{eq:adsorbedgasperton} to get the adsorbed OGIP in scf, i.e., $$\begin{equation} G_a =\hat{G}_a m_r = V_{SL} \frac{p}{p+p_{SL}} m_r \end{equation}$$

Total Compressibility when Adsorption is ON

In order to honor mass balance, it becomes necessary to modify total system compressibility when accounting for adsorption. Total system compressibility can be determined using the following equation:

$$\begin{equation} c_t = c_r + \left(1-S_{wc}\right)c_g + S_wc_w+\frac{\rho_b\rho_g^{sc}}{2000\phi\rho_{ga}}\frac{V_Lp}{p+p_L}\left[\left(\frac{62.428\rho_{ga}}{1000\rho_g^{sc}}B_g-1\right) \left(c_r+\frac{p_L}{p\left(p+p_L\right)}\right)-c_g\right] \end{equation}$$

The derivation of this equation is shown here and is contructed upon Ambrose et al.[1].

Adsorption in whitson⁺

By default, the adsorption feature is turned off for all the wells and is only available for use in gas wells. Here's how to activate the adsorption feature in whitson⁺ and set up the langmuir isotherm for your gas well:

2. Numerical Model

2.1 Gridding

The numerical model will have a gridding as shown in Fig. 3. The gridding is logarithmic in the y-direction, and in the x-direction beyond the fracture tip. From the wellbore to the fracture tip the gridding is uniform in the x-direction.

Fig. 3: Gridding of Numerical Model

The gridding is calculated based on the dimensions of the model. The gridding of the numerical model will is a backend feature, where the user can choose between low, medium, and high grid refinement. Determining the number of grid blocks for the chosen level of grid refinement is discussed in the next subsection. The formulas used for gridding are

$$\begin{equation} \Delta x_i = \frac{x_f}{N_{x,i}} \label{eq:dxunif} \end{equation}$$

$$\begin{equation} x_{o,j+1} = R_{x}x_{o,j},\quad R_x=\bigg(\frac{x_e-x_f}{x_0}\bigg)^{\frac{1}{N_{x,o}-1}}, \quad \Delta x_{o,j}=x_{o,j+1}-x_{o,j}, \quad j = 1,\dots,N_{x,o} \label{eq:dxlog} \end{equation}$$

$$\begin{equation} y_{j+1} = R_{y}y_{j},\quad R_y=\bigg(\frac{2y_e}{w_f}\bigg)^{\frac{1}{N_{y}-1}}, \quad \Delta y_{j+1} = y_{j+1}-y_j,\quad j = 1,\dots,N_{y} \label{eq:dylog} \end{equation}$$

where the total number of grid blocks in the model are \(N_t = (N_{x,i} + N_{x,o})N_y = N_xN_y\).

2.2 Grid Refinement

The number of grid blocks in the model is controlled by the grid-refinement level set by the user. There are four levels of grid refinement which allow the user to decide the level of "compromise" between simulation run time and level of detail captured in the simulation results:

1. Very Low (favours short simulation time)
2. Low
3. Medium
4. High (favours capturing the details)

An internal logic is used to translate the level of grid refinement to a number of grid blocks. We use average grid-block dimensions in the \(x\)- and \(y\)- directions to set the refinement of the gridding. The following table contains the fixed numbers for \(\bar{\Delta} x\) and \(\bar{\Delta} y\) at the three grid-refinement levels.

Property	\(\bar{\Delta} x\) (ft)	\(\bar{\Delta} y\) (ft)
Very Low	200	8
Low	50	2
Medium	25	1
High	12.5	0.5

The number of grid blocks in the \(x\)- and \(y\)- directions are then calculated as

$$\begin{equation} N_x = \bigg\lceil \frac{x_e}{\bar{\Delta} x}\bigg\rceil \end{equation}$$

$$\begin{equation} N_y = \bigg\lceil \frac{y_e}{\bar{\Delta} y} \bigg\rceil \end{equation}$$

The split of grid blocks in the \(x\)-direction \(N_{x,i}/N_x\) is linear with \(x_f/x_e\). Because the number of grid blocks have to be integers, we round the numbers as follows:

$$\begin{equation} N_{x,i} = \begin{cases} 0 & : \frac{x_f}{x_e} = 0\\ \big\lceil N_x\frac{x_f}{x_e}\big\rceil & : 0 < \frac{x_f}{x_e} < \frac{1}{2}\\ \big\lfloor N_x\frac{x_f}{x_e}\big\rfloor & : \frac{1}{2} \leq \frac{x_f}{x_e} < 1\\ N_x & : \frac{x_f}{x_e} = 1 \end{cases} \label{eq:gridlogic} \end{equation}$$ The number of grid blocks outside the fracture tip are then calculated by \(N_{x,o} = N_x - N_{x,i}\).

2.3 Grid Outputs - Pressure, Saturation 2D Maps

Grid refinement used in the previous section dictates the number of gridblocks used in the simulation model. Each gridblock can have the following results as outputs from the full-physics numerical simulation - pressure, oil, gas and water saturations - at discrete timesteps, spanning the simulated production history and forecast. Such maps with pressure and phase saturations for each gridblock can be used to estimate the drawdown and depletion across different parts of the model.

Choosing Grid Refinement and Using 2D Maps in whitson⁺

You can set whether you want to capture this information prior to running the simulation by toggling on the 2D Map button on the top-right of the screen - this will prompt you to rerun the simulation so that the results can be captured. Once the model is rerun, clicking the 2D Map button will open the pressure and saturation maps collected during the run.

You can visualize the results with 10 fractures together or look at a single fracture model in two ways:

• In bird's eye view, i.e. the x-y cross-section or each layer along the z direction in multi-layer models, and
• In side view, i.e. the z-y cross-section or layers along the x direction (i.e. fracture half-length, wellbore to fracture tip).

You can even set up fixed ranges for the colorbar manually, so that the colorbar limits do not change dynamically for each timestep.

Be sure to rerun the numerical model everytime you change the grid refinement since this sets up a new discretization of the model and the grid output maps will be different due to the difference in the number of gridblocks. Here's how to activate 2D maps - notice how using a higher grid refinement offers higher resolution maps with more gridblocks, compared to low or very low grid refinements in the GIF below:

2.4 Well Control

A well is always controlled by specifying a target rate. The most common rate is a surface product rate such as surface gas rate, surface oil rate, or surface water rate. Sometimes the target is a phase rate specified at flowing bottomhole conditions, either as a single-phase wellbore rate, or a combination of several wellbore phase rates, e.g. "reservoir" wellbore oil phase rate, "reservoir" wellbore liquid (oil phase + water phase ) phase rate or total wellbore fluid rate (gas phase + oil phase + water phase).

A zero target rate can also be specified, meaning that no production is seen at the surface. The well is "shut-in" at the surface. Downhole within the wellbore, considerable flow rates usually are found during the shut-in of a well with multiple well connections (to >1 grid cells). Some well connections show positive production rates and other well connections experience negative injection rates. The total injection rate of all components (surface gas, surface oil, surface water) must equal the sum of all well connection production product rates (to ensure no material balance loss in the wellbore during a shut-in time step).

The well tries to satisfy the target rate during a time step, but only if the specified pressure constraint is not violated. Typical pressure constraints include flowing bottomhole pressure or flowing tubing pressure. If the pressure constraint is reached then the target rate can not be met and a rate is chosen that ensures the pressure constraint exists in the well.

During zero target rate and STOP (i.e. well closed at the surface), the pressure constraint will be honored. Layer crossflow may happen if the well is connected to multiple numerical layers with differential depletions. During zero target rate and SHUT (i.e. well closed at the sand face), the well is isolated, no well constraint is enforced.

A producing well can also have constraints on the well's produced surface product ratios GOR, WOR, OGR, surface water cut of total liquid rate or reservoir wellbore phase fractions such as water cut. These constraints are usually maximum values which, if reached, the wellbore pressure is adjusted to honor the constraint, and accordingly not allow the target rate to be met.

Well Control in whitson⁺

There are six options currently available for controlling wells:

• Oil: the maximum surface oil production rate target or contraint.
• Gas : the maximum surface gas production rate target or constraint.
• Water : the maximum surface water production rate target or constraint.
• Liquid : the maximum surface liquid rate (water + oil) production rate target or constraint.
• BHP: the minimum bottomhole pressure taget or constraint
• BHP (synthetic): bottomhole pressure profile target or constraint, offering an option to include a maximum rate contraint. The BHP profile is set upon user-defined inputs such as (a) Minimum BHP, (b) Time to Minimum BHP, and (c) Total Simulation Days.

During the historical period, the well is controlled on the user-selected option. If the well is controlled by one of the surface-rate targets, then a BHP constraint of 100 psia is applied. If the well is controlled on a BHP target, then the software will set an unrealistic rate target with the desired BHP profile as a lower limit for producers. For the synthetic BHP profile, there has, since the Sept. 2023 release of whitson⁺, been an option of setting a rate constraint.

During shut-ins period, the status of the well is set to STOP, indicating no fluid production to the surface and potential layer crossflow may occur if there are any open connections.

During the forecast period, the well is consistently controlled based on either a BHP or WHP (CHP or THP) target, with the added flexibility of applying a maximum rate constraint. If none of rate constraint is chosen, then the rate will be set to an unrealistic target.

It is important to note that whitson⁺ does not support "Reservoir" or bottomhole-rates targets. Additionally, constraining the well based on producing ratios (GOR, WOR, OGR, GLR, etc.) is also not supported. No economic criteria for production wells are currently being enforced. This implies that the well will only be shut-in (denoted by a well status of STOP) if the well has zero rates and/or the pressure falls below the predefined minimum bottomhole pressure (whitson⁺ default is 100 psia).

Should your company require any of these constraint options, please feel free to contact us or use the Send Feedback button at the top right of whitson⁺.

How does whitson⁺ recognize a shut-in?

If Well Control is ,

• Oil: well is shut-in if oil rate for time step is 0.
• Gas: well is shut-in if gas rate for time step is 0.
• Water : well is shut-in if water rate for time step is 0.
• Liquid : well is shut-in if liquid rate (oil + water) for time step is 0.
• BHP: well is shut-in if all rates (oil + gas + water) for time step is 0.
  PS! Should all the rates for all time steps be uniformly zero, the software assumes that the user would like to control the model on a custom, uploaded BHP profile. Consequently, the well won't be considered as shut-in.

2.5 Time Stepping

The selected well control and grid refinement is used to run the simulation model and Time-Stepping dictates how many timesteps should be passed to the simulator.

Higher number of time-steps takes longer to run since the simulator tries to match the given well control for all these time steps. A significant reduction of the model run-times can be achieved with a negligible trade off in model accuracy - which is especially useful for wells with long, noisy producing history or BHP. Here are the available options to control the number of timesteps to use for simulation:

1. All - Simulates every uploaded timestep.
2. Smart - Simulates daily timesteps for the first 100 days and then every 10th point after that.
3. Custom - Simulates every Nth timestep, where you can specify 'N'. Example if you set N=7, the simulator simulates weekly timesteps.

Did you notice how the model runs faster with fewer timesteps to simulate?

3. What affects producing GOR profile and how?

3.1 Reservoir Parameters

We observe a wide-range of producing GOR profiles in tight unconventionals. But which reservoir parameters change producing GOR when the bottomhole pressure is below the saturation pressure? And how?

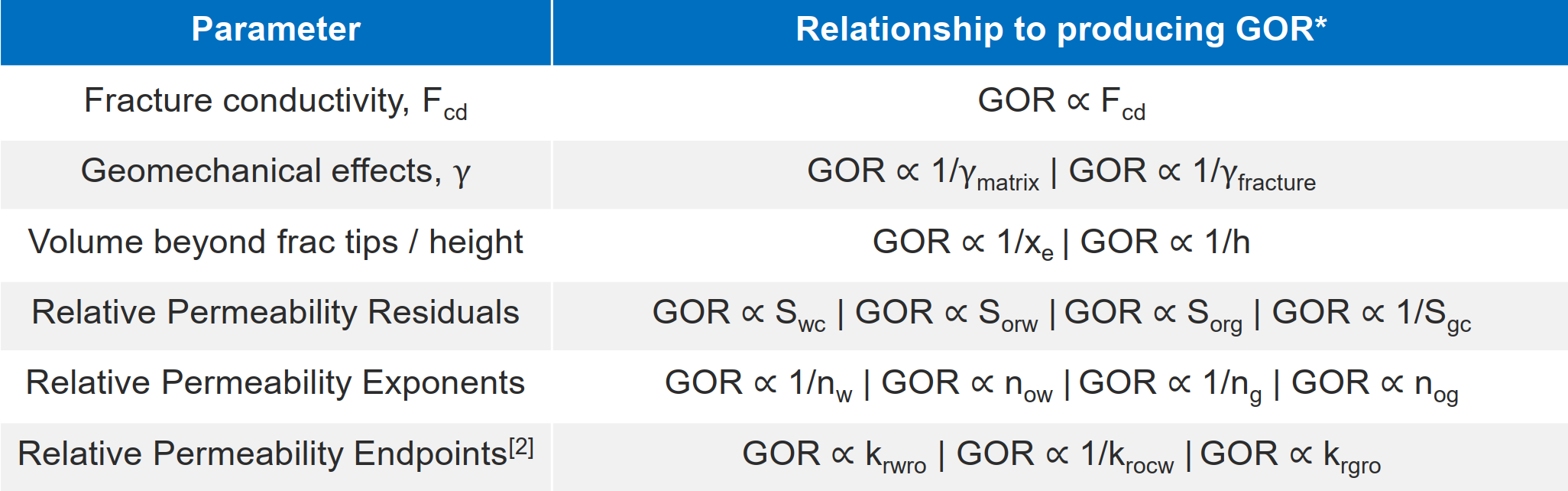
Fig. 4: Effects of Reservoir Parameters on producing GOR

There are four broad categories of reservoir parameters that impact producing GOR

• Fracture conductivity
• Geomechanical effect
• Contributing volume beyond frac tips / height ("unstimulated rock")
• Relative permeability

This is summarized in the table above. Read more in this slide deck →→here←←.

3.2 Flow Regime

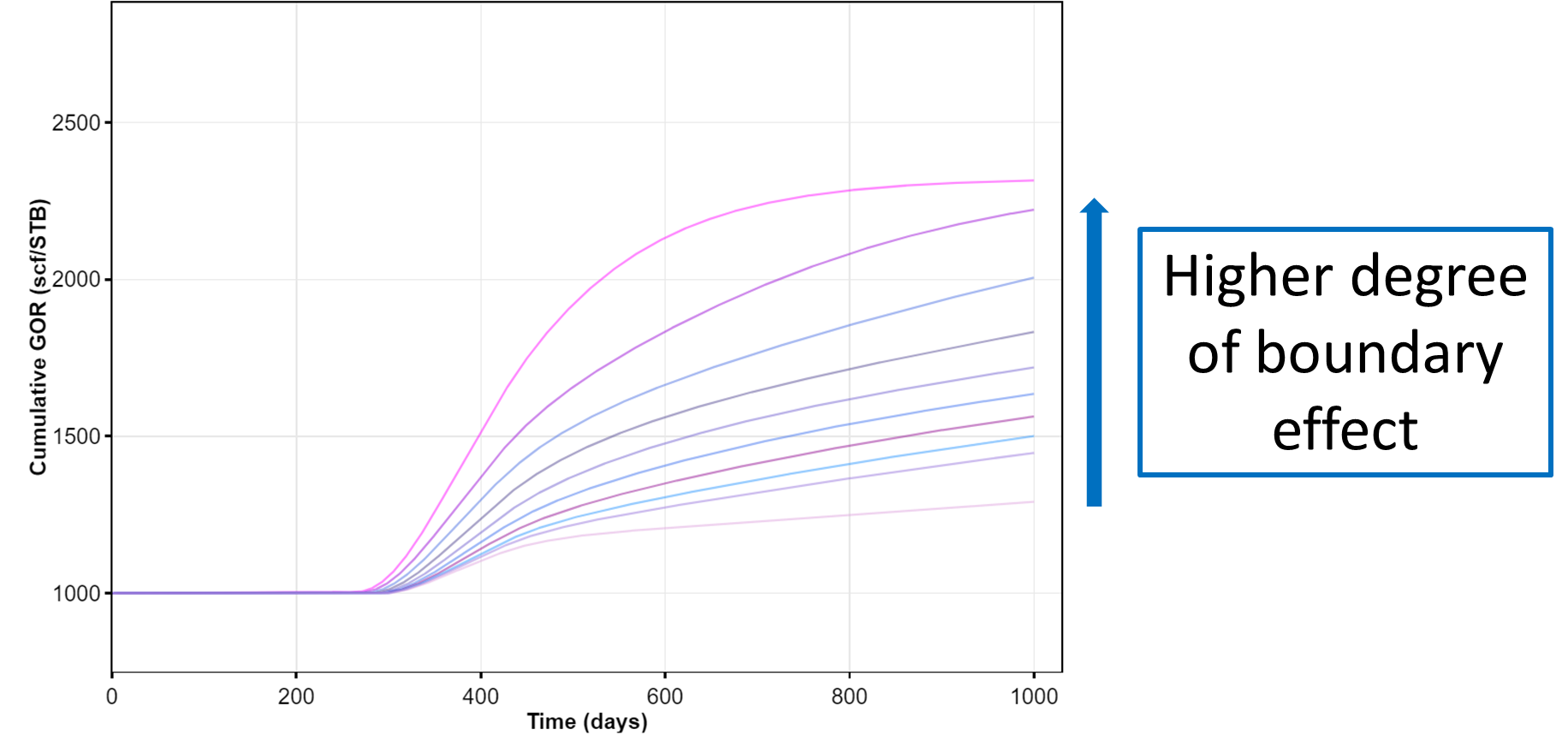
Fig. 5: Effects of flow regime and boundaries on producing GOR profile.

In addition to the reservoir parameters outlined above, flow regime matters. Everything else being equal producing GOR follows this relationship below saturation pressure:

$$\begin{equation} GOR_{p,IA} < GOR_{p,TF} < GOR_{p,BDF} \end{equation}$$

Where IA refers to infinite acting, TF refers to transitional flow and BDF refers to boundary dominated flow.

4. Forecast

Once the production history is matched, the results can be used to forecast the production. In whitson+, the simulation forecast is controlled by pressure (i.e. BHP or WHP).

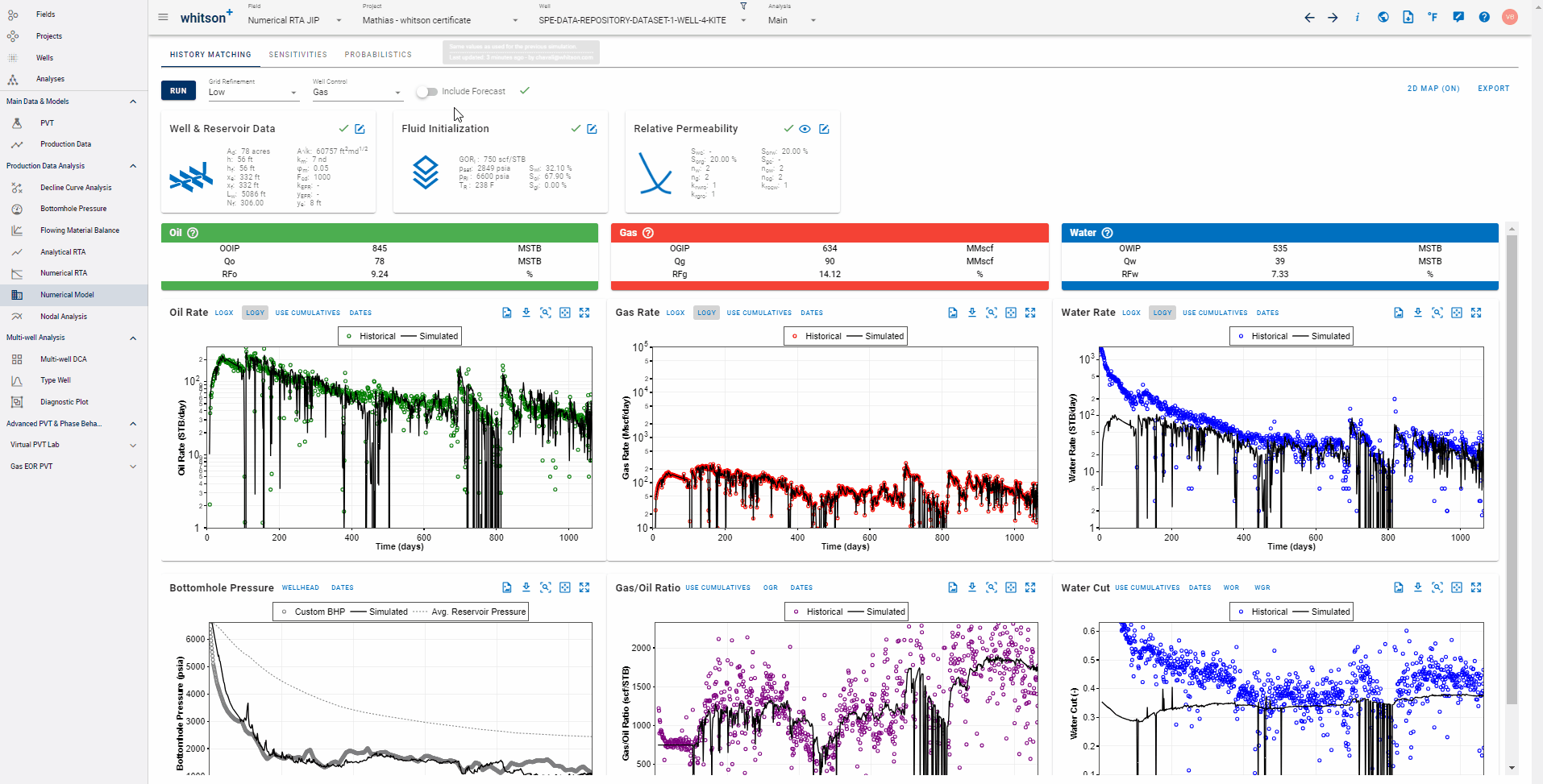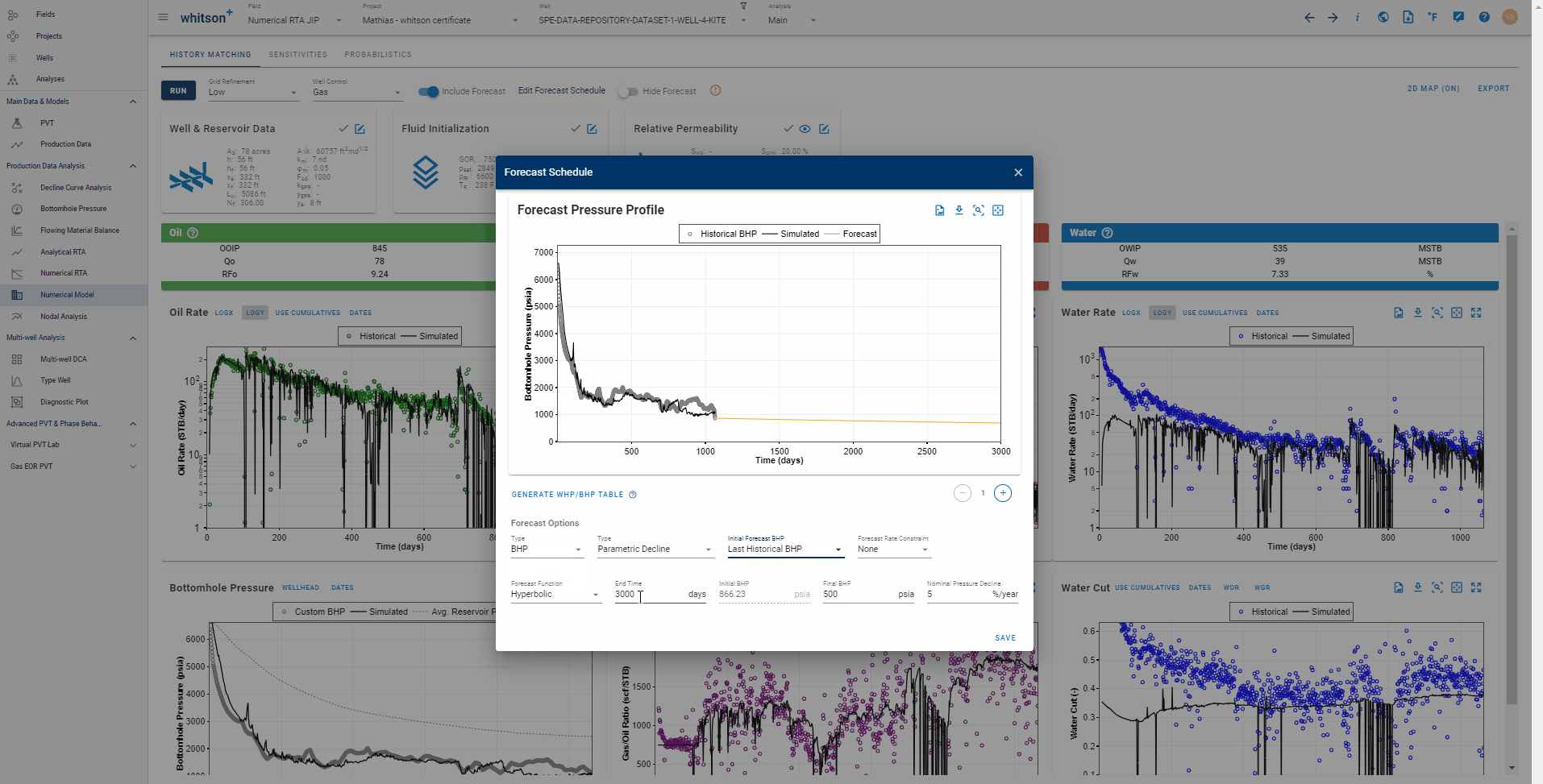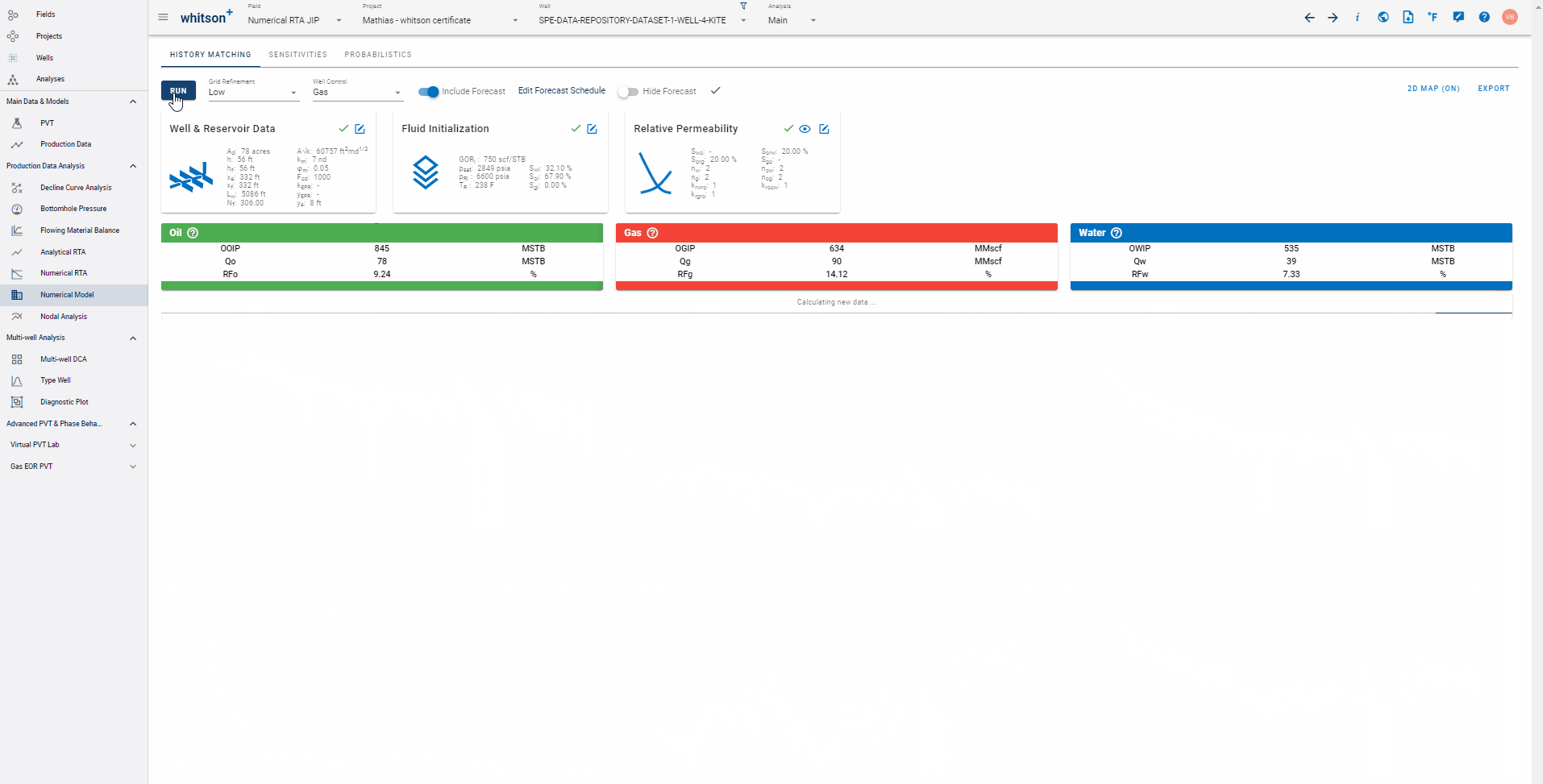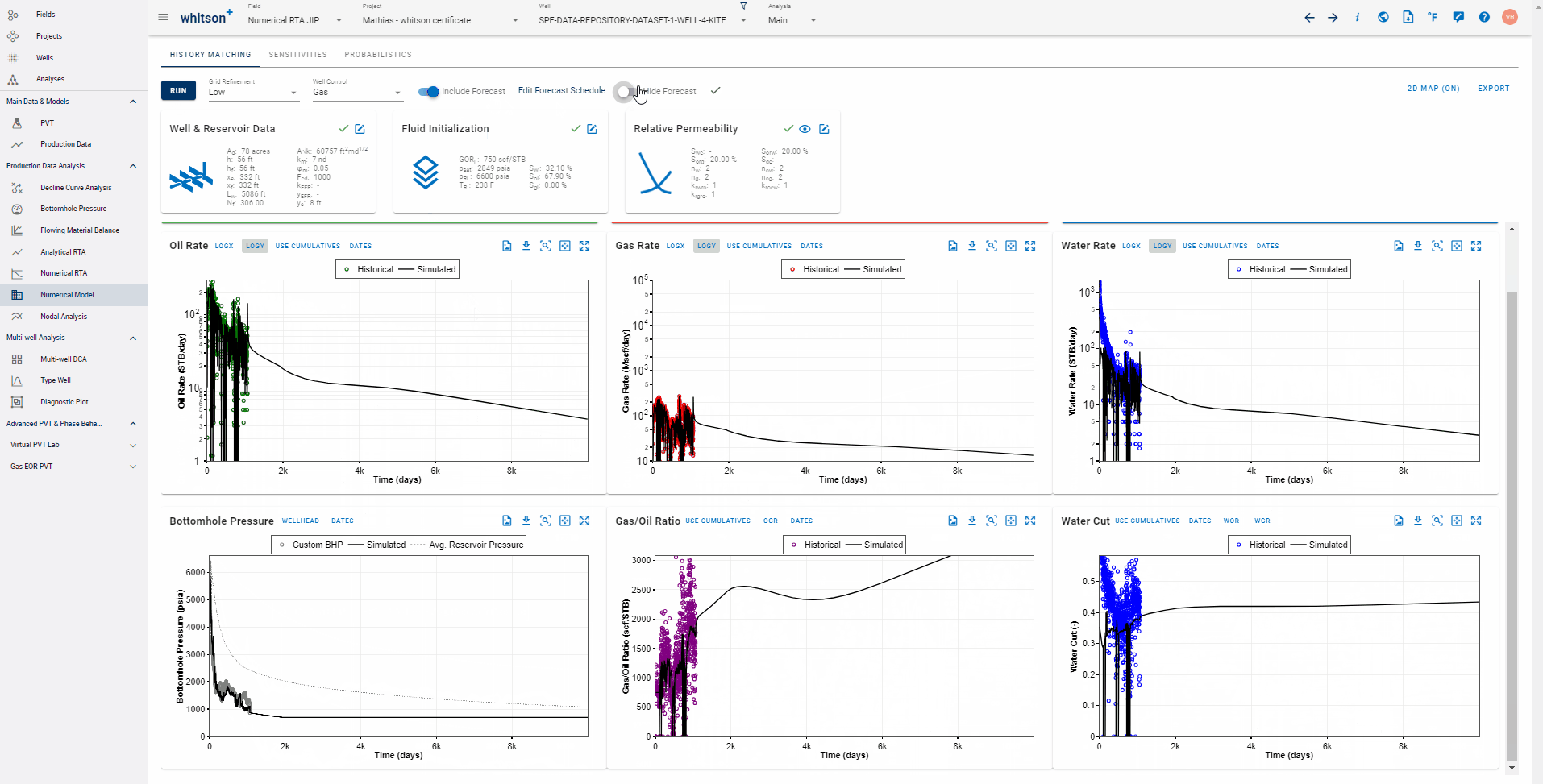
Fig. 6: Forecasting the numerical model

4.1 BHP Forecast Type

Whitson+ provides three alternatives in creating BHP forecast:

1. Parametric Decline to set the forecasting function between the input initial and final BHP as hyperbolic or linear based on the input Nominal Pressure Decline in %/yr or psia/d, respectively.

2. Constant BHP throughout simulation time.

3. Custom Schedule provided by user in table-wise manner. By default, the first row will be the BHP at the last time step of history matching simulation run.

4.2 WHP Forecast Type

Whitson+ provides three alternatives in creating WHP forecast:

1. Parametric Decline to set the forecasting function between the input initial and final WHP as hyperbolic or linear based on the input Nominal Pressure Decline in %/yr or psia/d, respectively.

2. Constant WHP throughout simulation time.

3. Custom Schedule provided by user in table-wise manner. By default, the first row will be the WHP at the last time step of history matching simulation run.

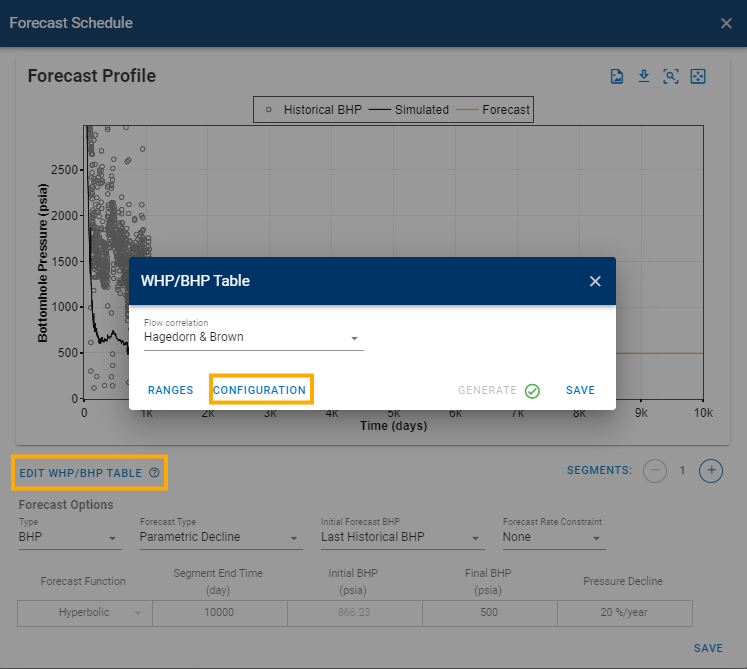
4.3 Edit WHP/BHP Table

The WHP/BHP table is used to:

• Compute the WHP when forecasting on a BHP profile.

• Compute the BHP when forecasting on a THP profile.

The flow correlation and wellbore configuration are editable for the forecast period, as shown below.

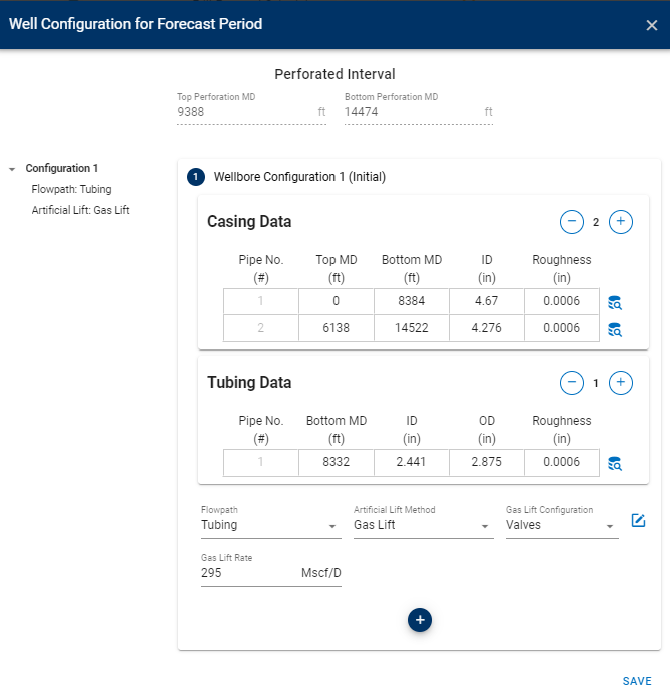
5. Autofit

5.1 How to run Autofit

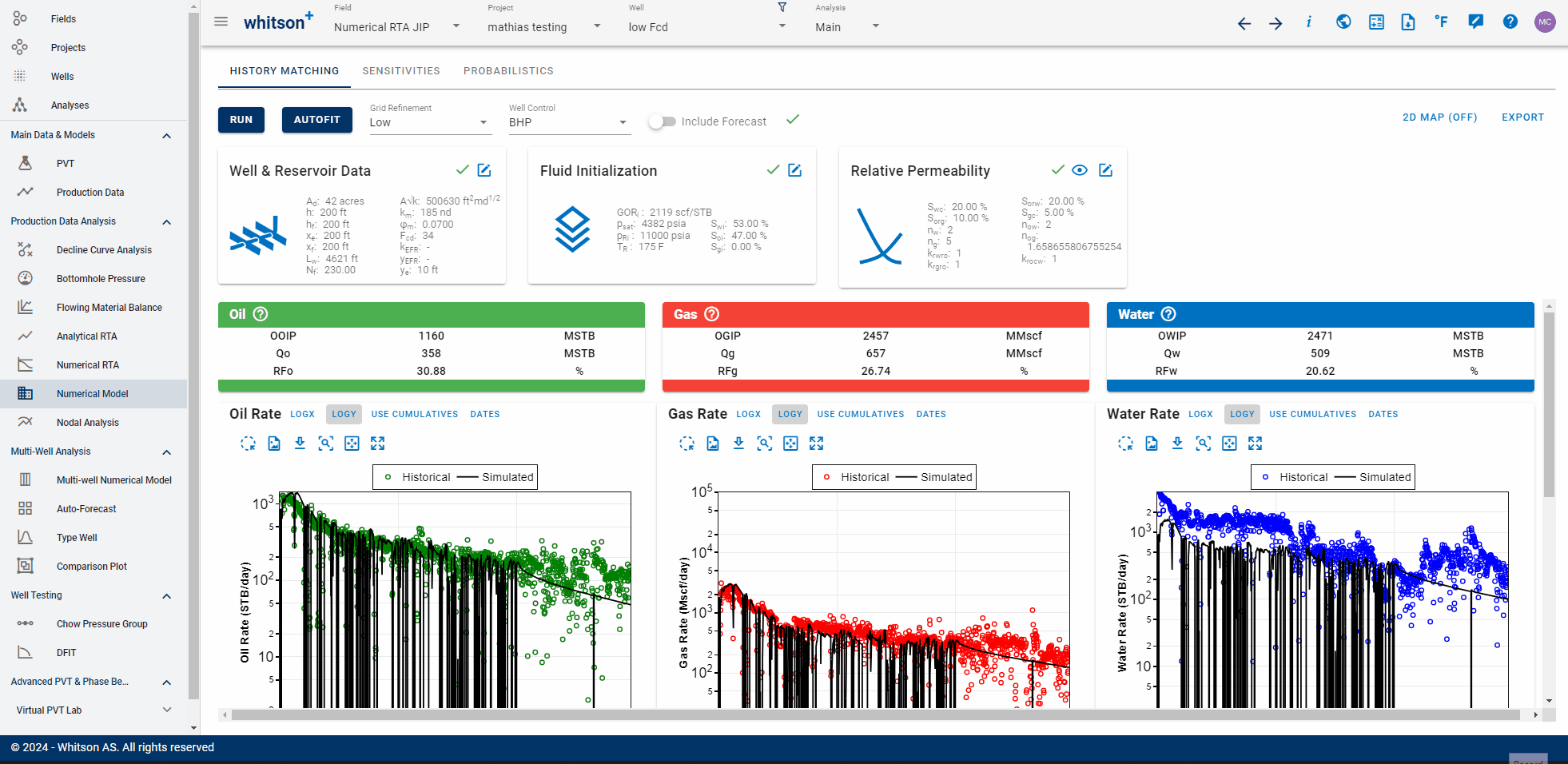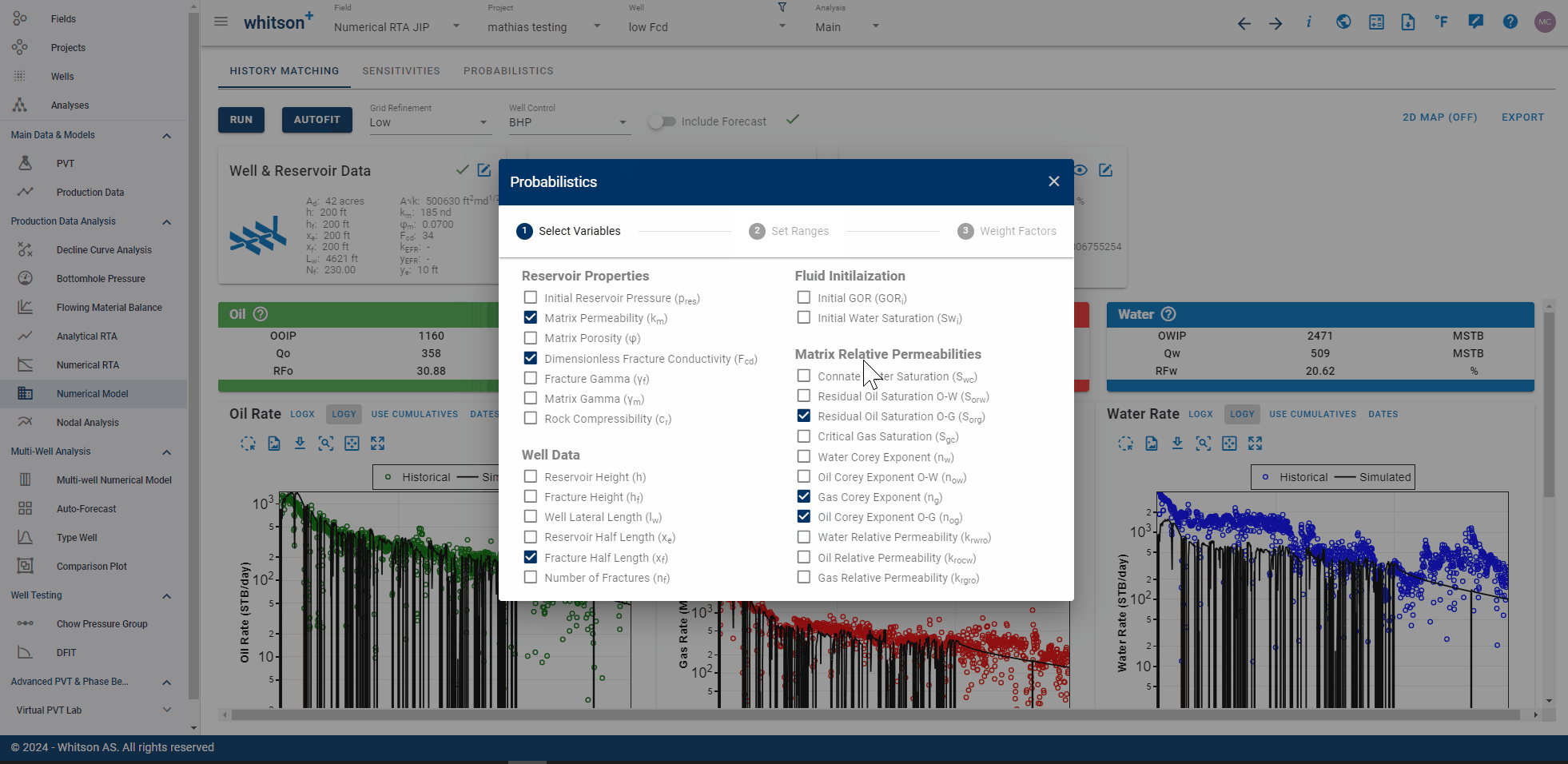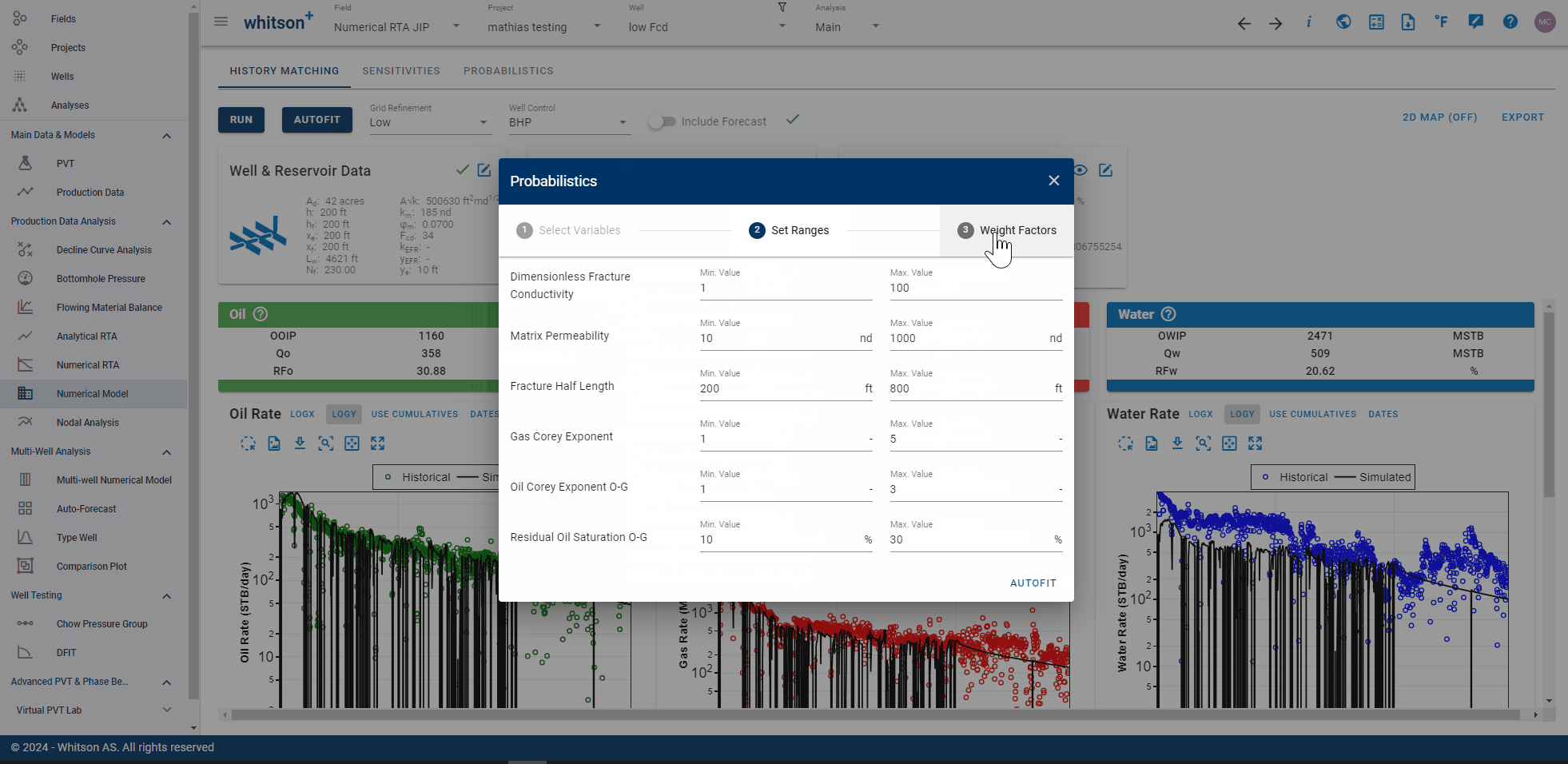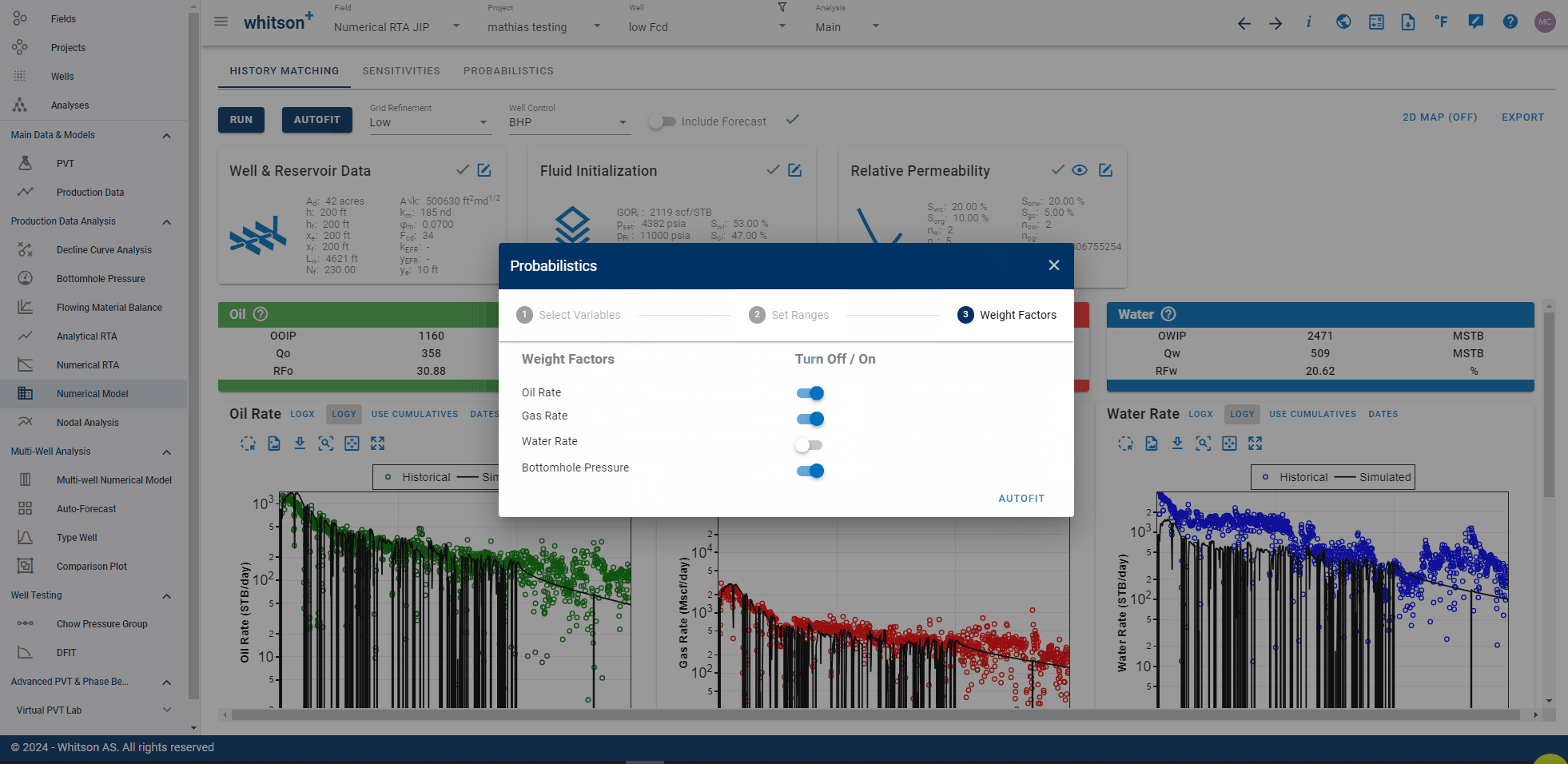
It is possible to automatically history match a numerical model to historical data with the "Autofit" option. To run the "Autofit",

1. Click the AUTOFIT-button to the upper left.
2. Select parameters you would like to alter (\(x_f\) and \(k\) are defaults).
3. Provide their ranges for each parameter.
4. Turn on/off weighting for relevant timeseries (global weighting switch).
5. Click AUTOFIT to the lower right.

5.2 Set Weighting Points

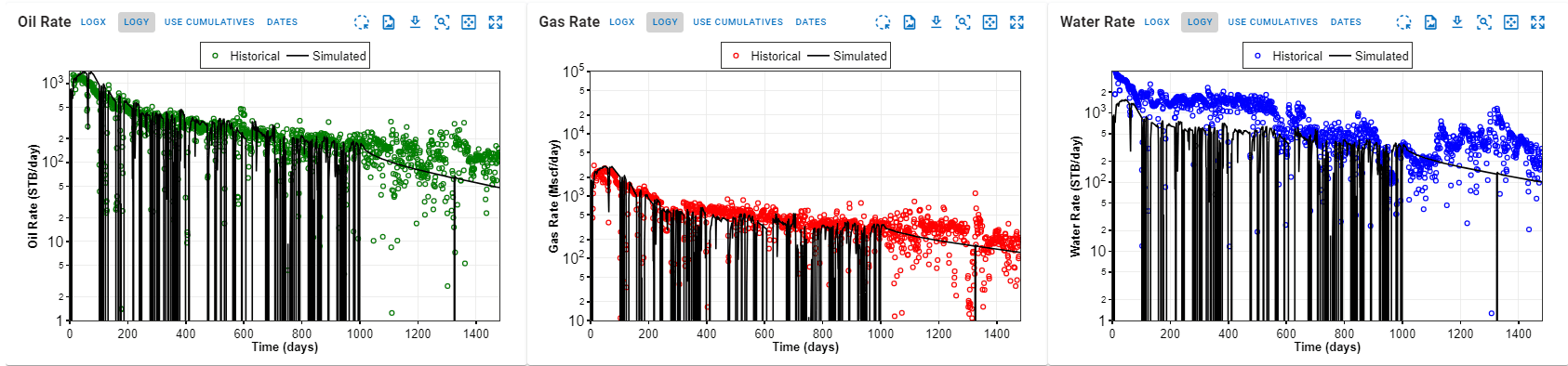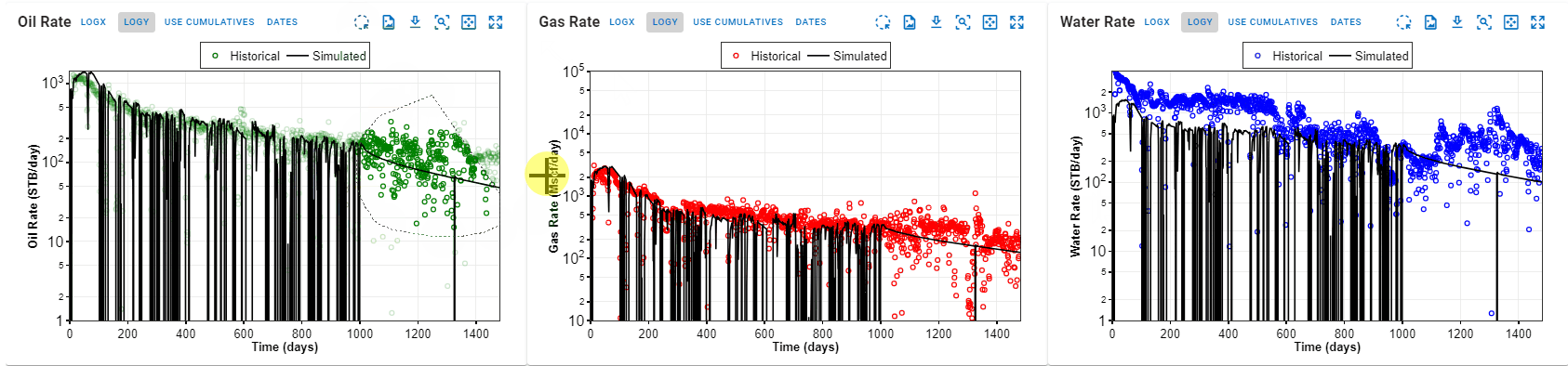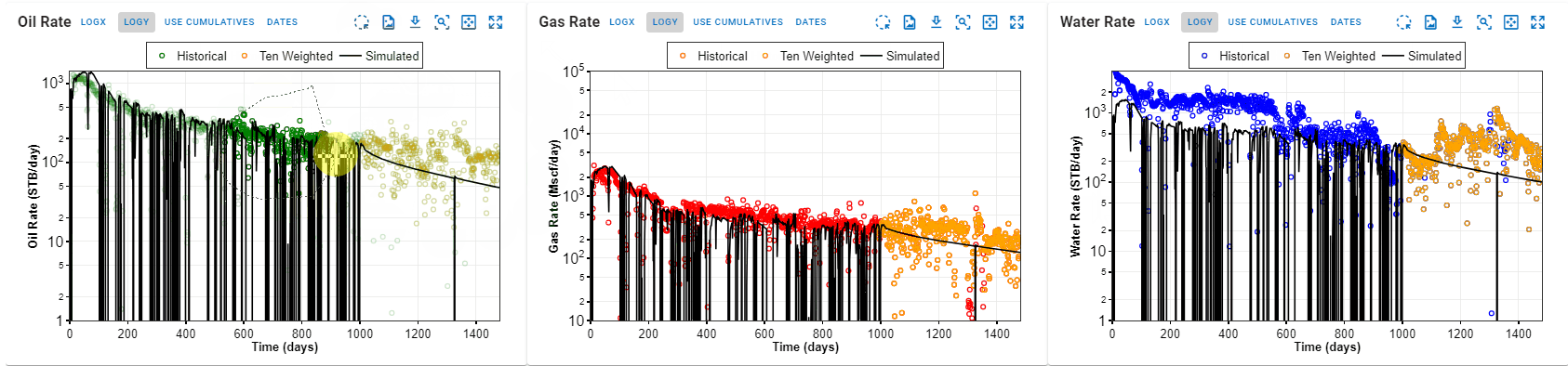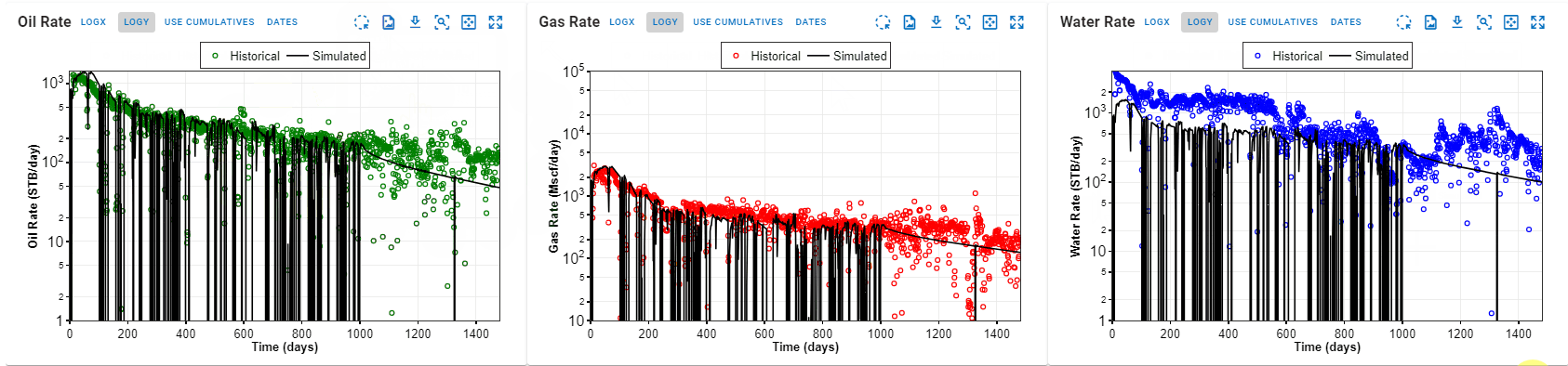
In addition to the global weighting switch, you can set different weighting throughout time.

Each timestep can be set to either

1. Weight = 1 (default)
2. Weight = 10 (considered important data to match)
3. Weight = 0 (considered less "bad data")

What is a weighting factor?

A weighting factor is a numerical parameter that assigns importance to data points during mathematical optimization, here in history matching numerical models to observed data. It helps prioritize or de-prioritize specific data points, optimizing model parameters for a more accurate fit.

5.3 Weighting & Error Calculation

whitson⁺ facilitates regression on parameters to minimize the sum of squares of weighted residuals in the context of observed data and corresponding predictions. The objective function in is defined as:

$$\chi^2 = \sum_{i=1}^{N} (r_i w_i)^2$$

Here, $r_i$ represents the RMS residual error between observed measurement $i$ and its corresponding prediction, while $w_i$ is the user-assigned weighting factor for that residual. Ideally, these weighting factors should be inversely proportional to the standard deviations of the residuals. Minimizing $\chi^2$ in provides the maximum likelihood estimation of the model parameters, assuming independent and normally distributed residuals.

The default weighting factors are 1, while they can also be set to 0 (no importance), and 10 (high importance). Reported is a root-mean-square (RMS) residual error ($E_{\text{RMS}}$) defined as:

$$E_{\text{RMS}} = \sqrt{\frac{\chi^2}{\sum_{i=1}^{N} (w_i)^2}}$$

This metric is related to $\chi^2$ but is more easily interpreted.

The residuals are calculated as relative percentages using the formula:

$$E_i = \frac{100(y_{i,\text{hist}} - y_{i,\text{sim}})}{y_{i,\text{hist}}}$$

where $y_{i,\text{hist}}$ is the historical production value, $y_{i,\text{sim}}$ is the simulated value, and $y_{i,\text{hist}}$ is the reference value for observation $i$. Historical production values that is 0 is excluded from the error calculation, while historical production values that has a higher error than 100% is set to 100% error (to avoid that individual outliers dominate the whole error calculation). A failed numerical run is attributed an error of 101%, ensuring that successful cases are always favored

5.4 Optimization Algorithm: Nelder-Mead

Nelder-Mead Simplex is a modified version of the downhill Simplex method used for non-linear regression in reservoir simulation. It enhances convergence by applying constraints on parameters during the search, checking estimates against preset limits. After convergence, the routine restarts with a slight perturbation to avoid local minima, ensuring a global minimum. While it may require more function evaluations, its simplicity and lack of derivative requirements make it robust under various conditions.

5.5 Optimization Heuristics

In pursuit of practicality, our approach involves modeling 50 historical data points in each iteration, ensuring fast run times of each individual numerical run. he objective of the minimization function is to align production cumulatives (considering weighting) and bottomhole pressures over time.

6. Refrac Analysis

A ‘refrac’ or refracturing treatment refers to the process of performing another hydraulic fracturing operation on a well that has already undergone the process in the past.

Typically, you may want to evaluate a refrac that was recently performed on one of the wells. To do that, use the MFMB feature - The workflow is outlined in this section here.

Sometimes, you also want to be able to predict the initial rates and subsequent decline for a refrac that is planned on a well in the future. To do that, use numerical modeling as shown below.

6.1 Workflow for estimating uplift on planned refracs

This section outlines our recommendation for what the simplified workflow could be -

1. History match the target well using BHP as Well Control and resolve a numerical model with high confidence.Then forecast this model to generate a baseline future expectation from the well, under current conditions as shown above in section 4 above.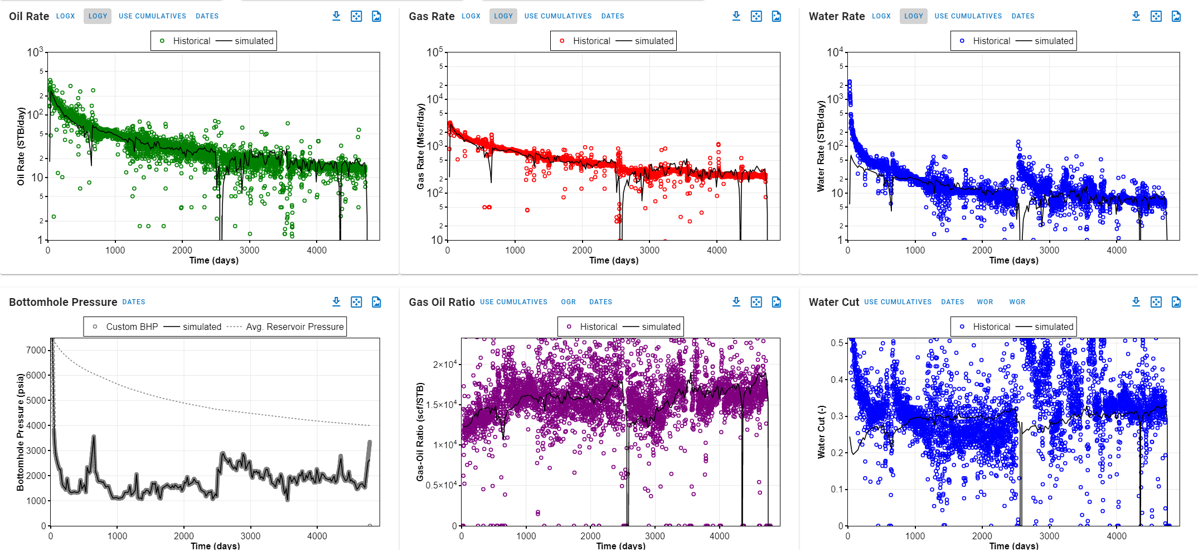

   
   Fig. 7: High confidence history matched numerical model

2. Copy the well (Wells page --> Click the three dots to the right of the well name --> Copy well)
   

3. On the copy of the well, continue using BHP as Well Control and modify the numerical model to reflect the expectation from the refrac, i.e. -
   a. Change the completion - increase the number of fractures (Nf) or fracture half-length (xf) or both.
   b. Increasing Nf will primarily accelerate depletion but yeild a higher intial rate.
   c. Increasing xf (if we expect a bigger refrac completion) will add additional pore volume
   d. Forecast this updated model.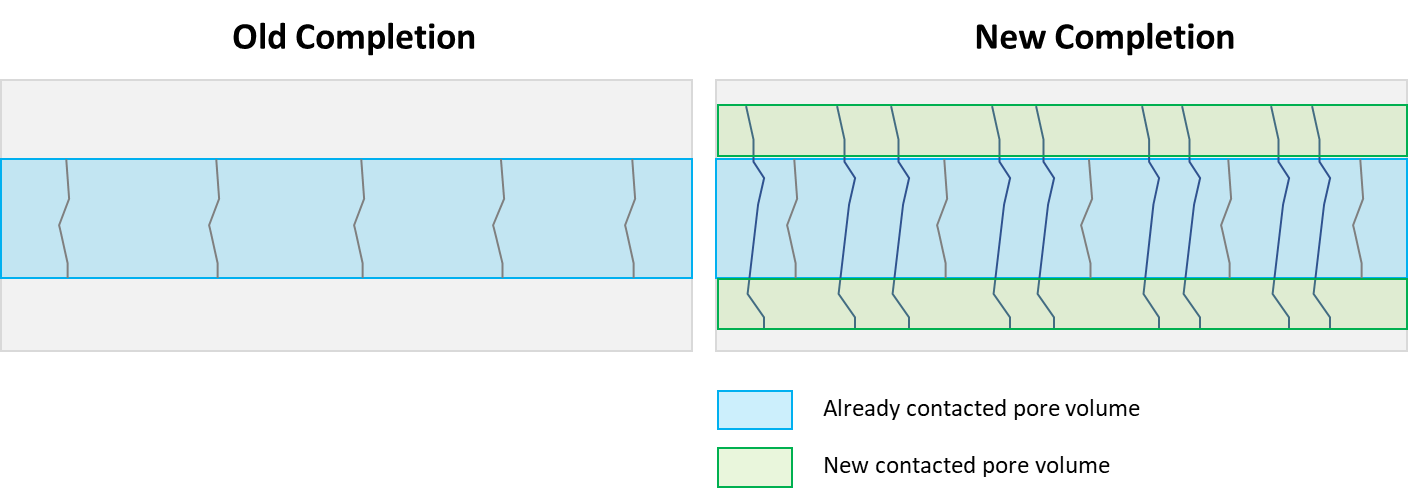
   

   
   Fig. 8: Updating the baseline numerical model

4. Delta between outcomes of Steps 1 and 2 is the refrac potential of this well.

5. Superpose these resulting rates at the time of refrac to get the uplift expected after refrac

   
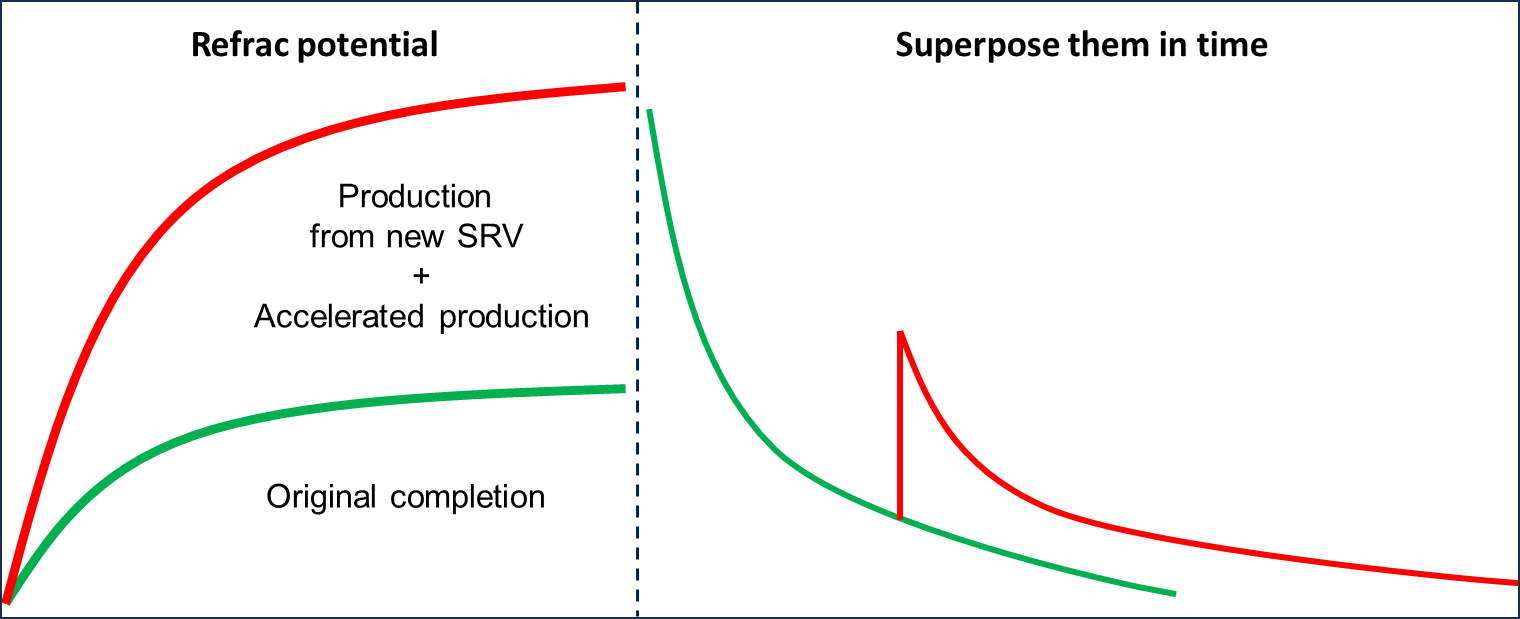
   Fig. 9: Forecasting the updated model and evaluating uplift

7. Sensitivities on Tubing/Casing Sizes with the Numerical Model

Sensitivity analysis of tubing/casing sizes can be done in the software using tubing tables within the numerical model. This allows imposing a surface pressure constraint.

Tubing tables are only applicable for the forecast period

However, to apply sensitivity analysis to the historical period, a workaround can be employed. This involves creating a new well without historical data and utilizing the forecast section to reproduce the observed surface pressures. The following steps outline the workaround:

1. Copy the well: Create a copy of the original well.
2. PVT: Initialize PVT
3. Remove historical data: Delete the existing production data from the copied well.

4. Match wellhead pressure: Replicate the observed wellhead pressure profile in the forecast profile of the copied well.

   
   

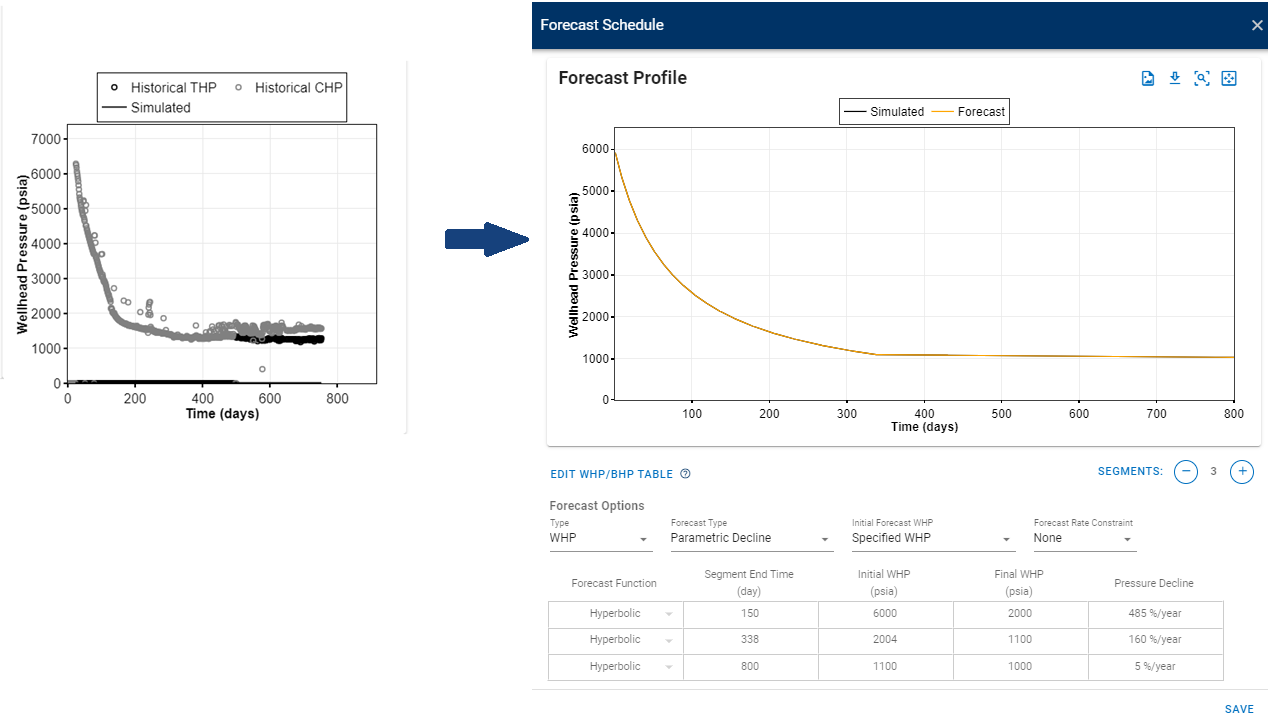
5. Modify tubing table: Adjust the configuration of the WHP/BHP table (tubing tables) to analyze the effects of different configurations.

   
   
   
   

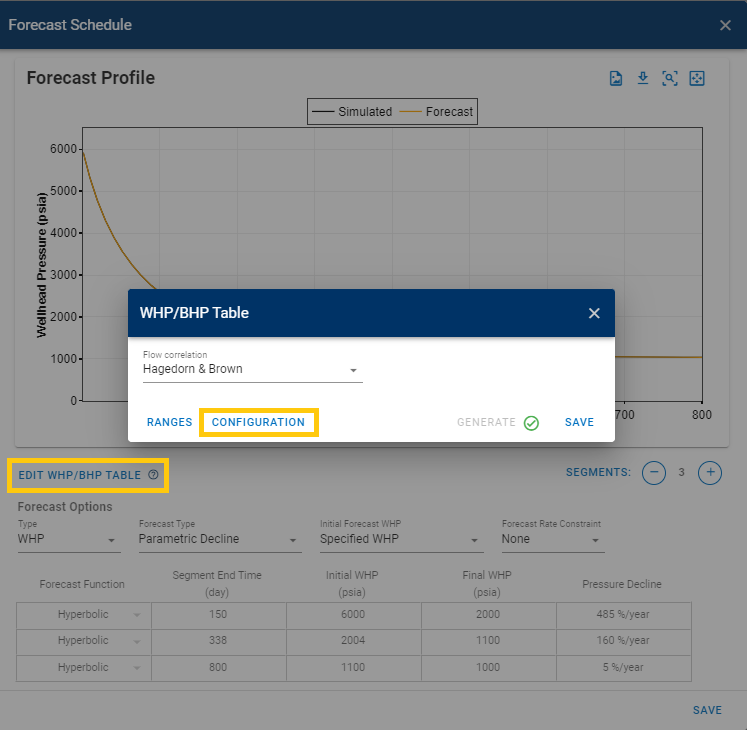
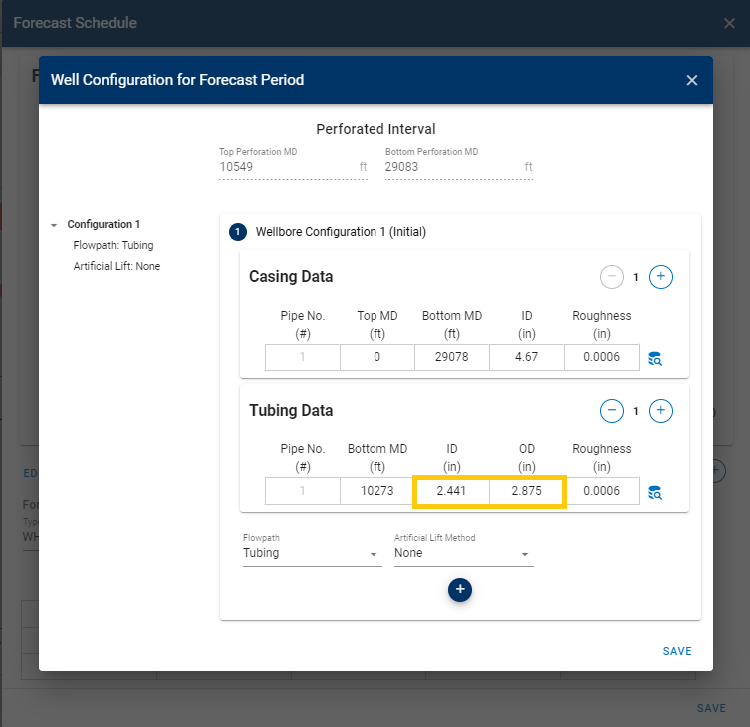
6. Run WHP forecast simulation: Run the numerical model in WHP type for the forecast option.

   
   

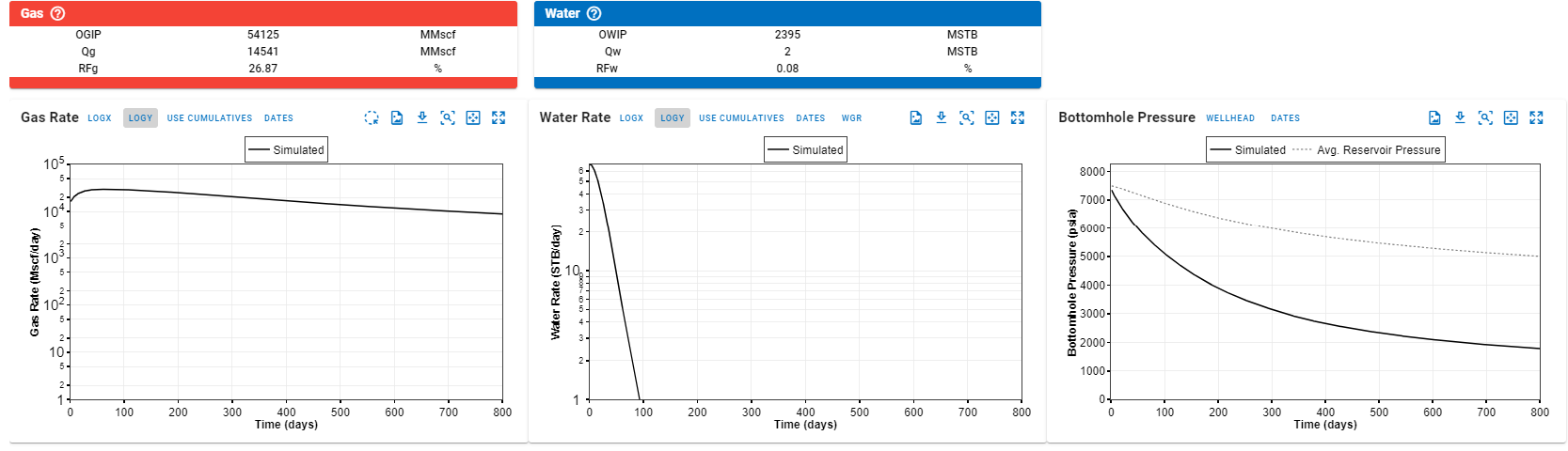
7. Repeat for other tubing sizes: Create new scenarios and repeat steps 5-6 for each tubing size you want to analyze.

   
   

8. Compare results: Use a comparison plot to visualize the results from all the sensitivity run.

   
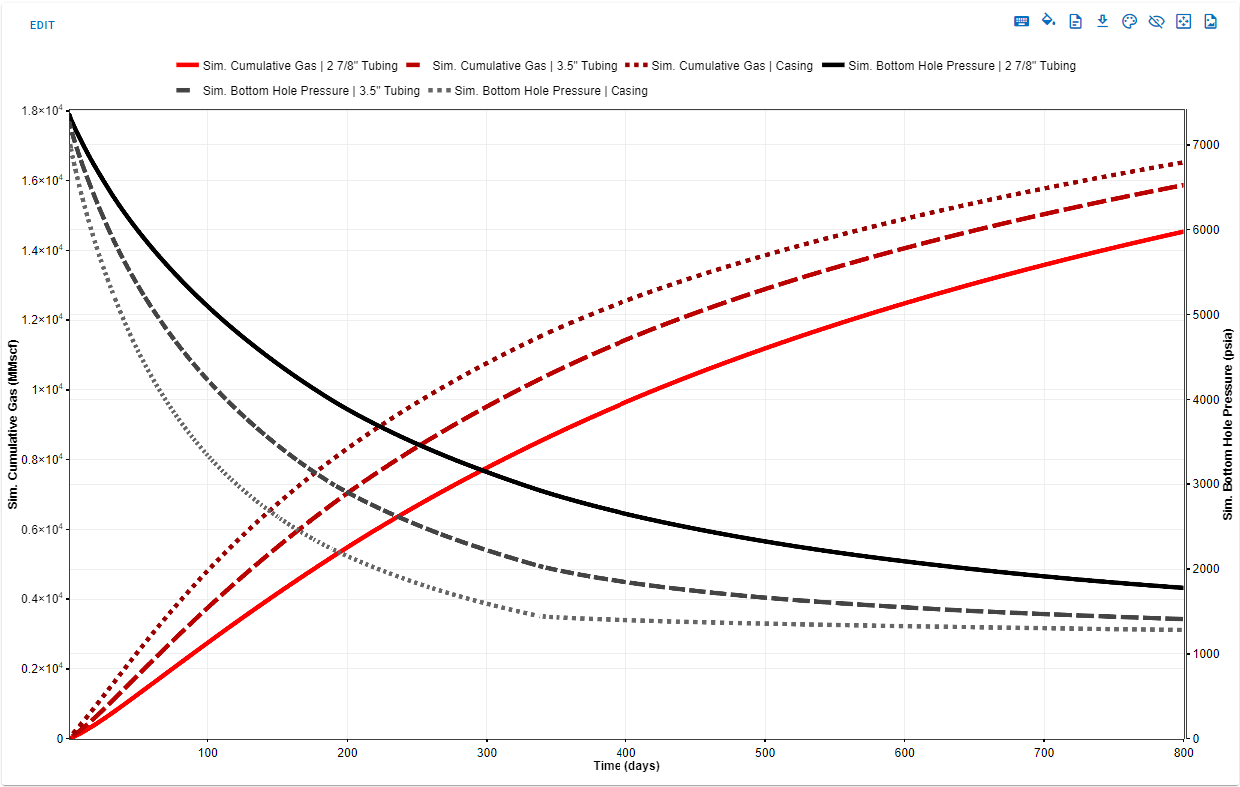
   Fig. 10: Cumulative gas profiles and bottomhole pressure profiles for all the scenarios

8. Saltwater Disposal Injection Well: History Matching Workflow

1. Upload the required data for this analysis: water injection rates, tubing/casing pressure, tubing/casing configuration, and well deviation survey.

2. Initialize PVT the default PVT. While the PVT isn't directly relevant to this specific analysis, running this process is a prerequisite for the following modules.

3. To model the bottomhole pressure during an injection process, it is necessary to activate the BHP injection mode. This is done in the Calculation Settings in the Well Data card (see .gif below). When enabled, this switch allows to simulate the pressure at the bottom of the wellbore during injection and all uploaded rates will be assumed to be injected rates.

   
   

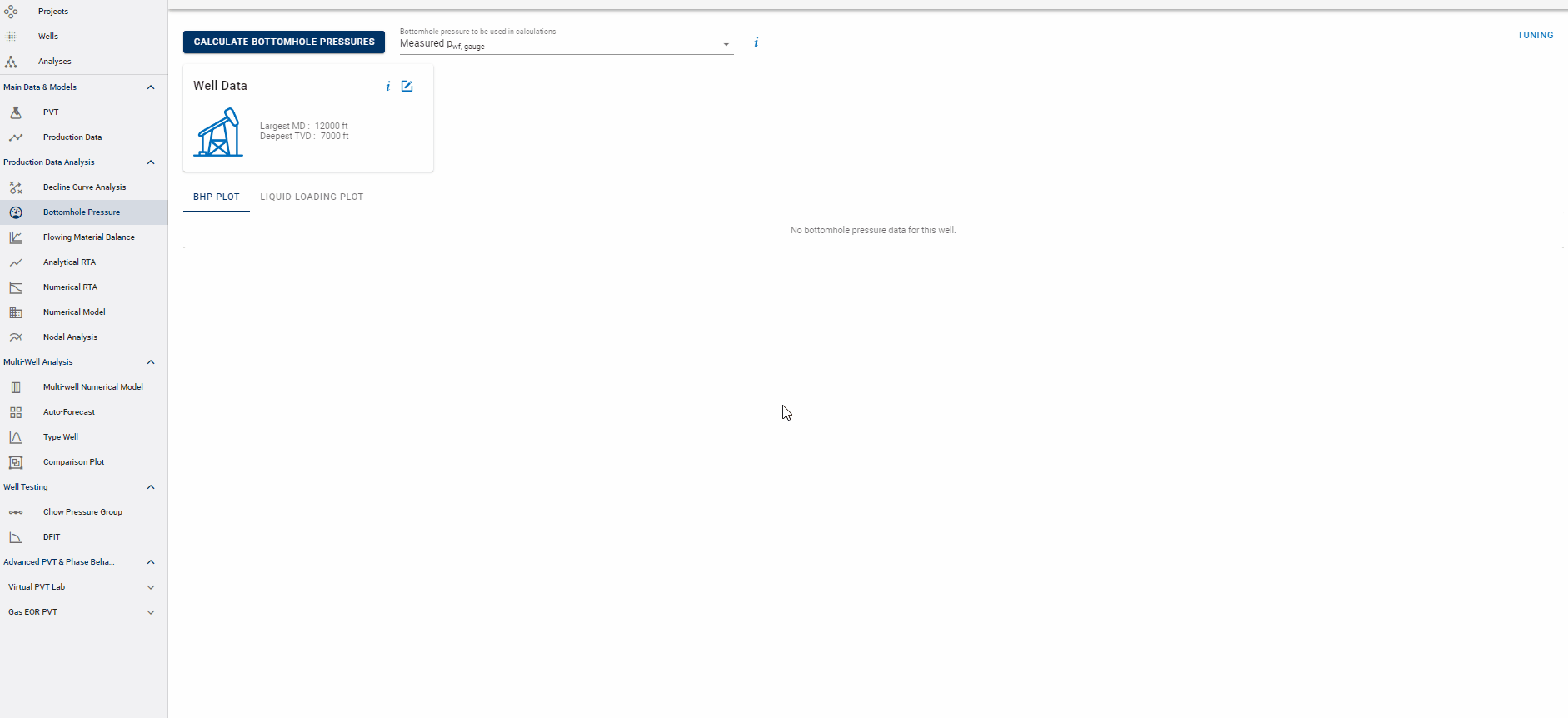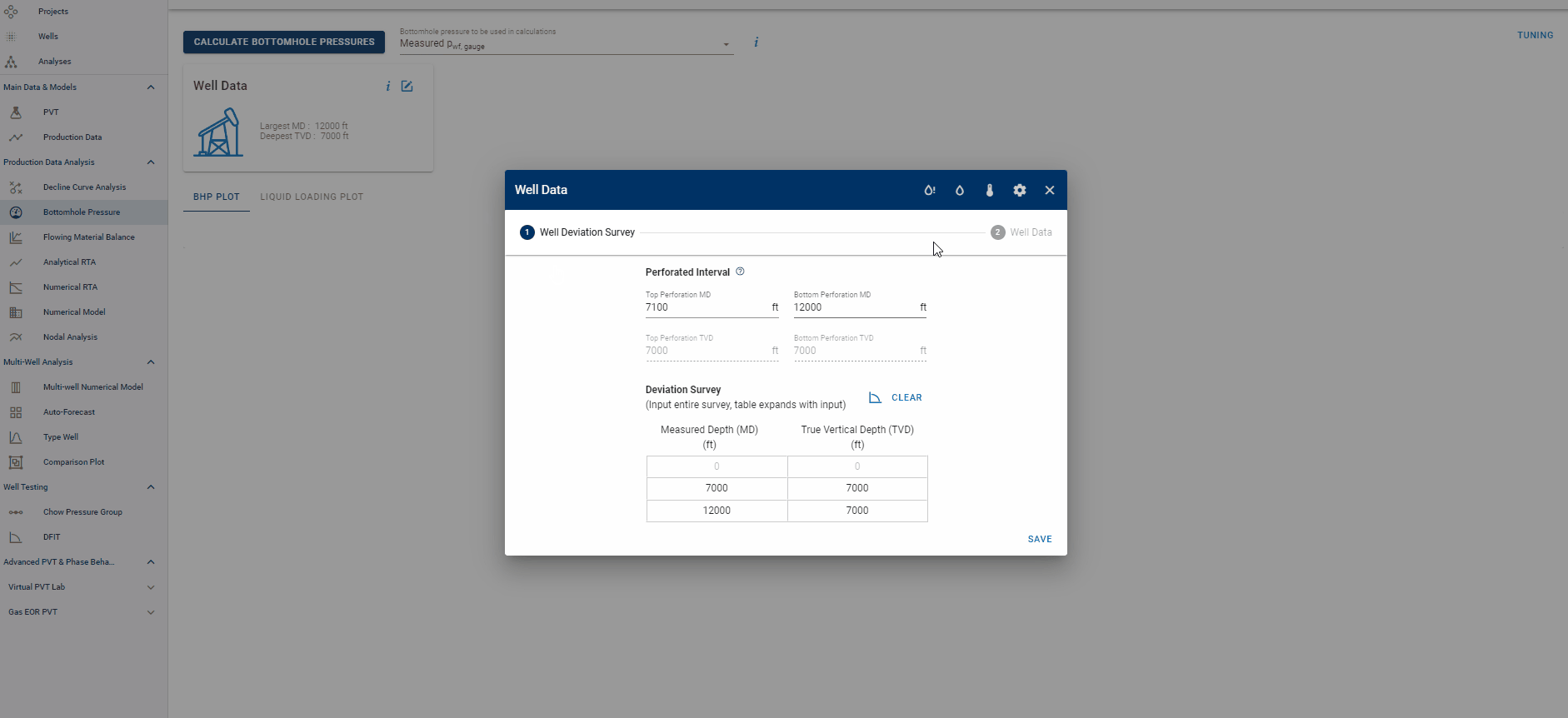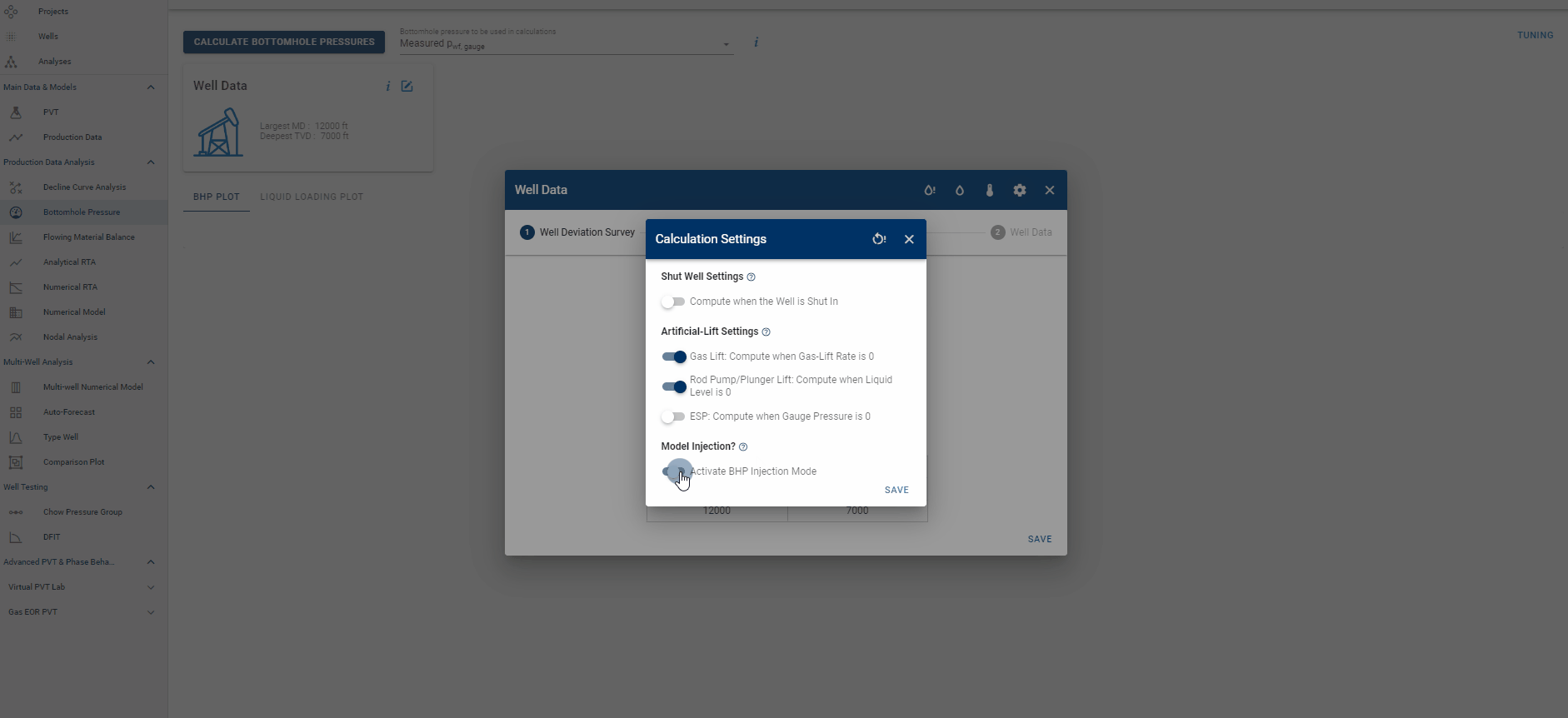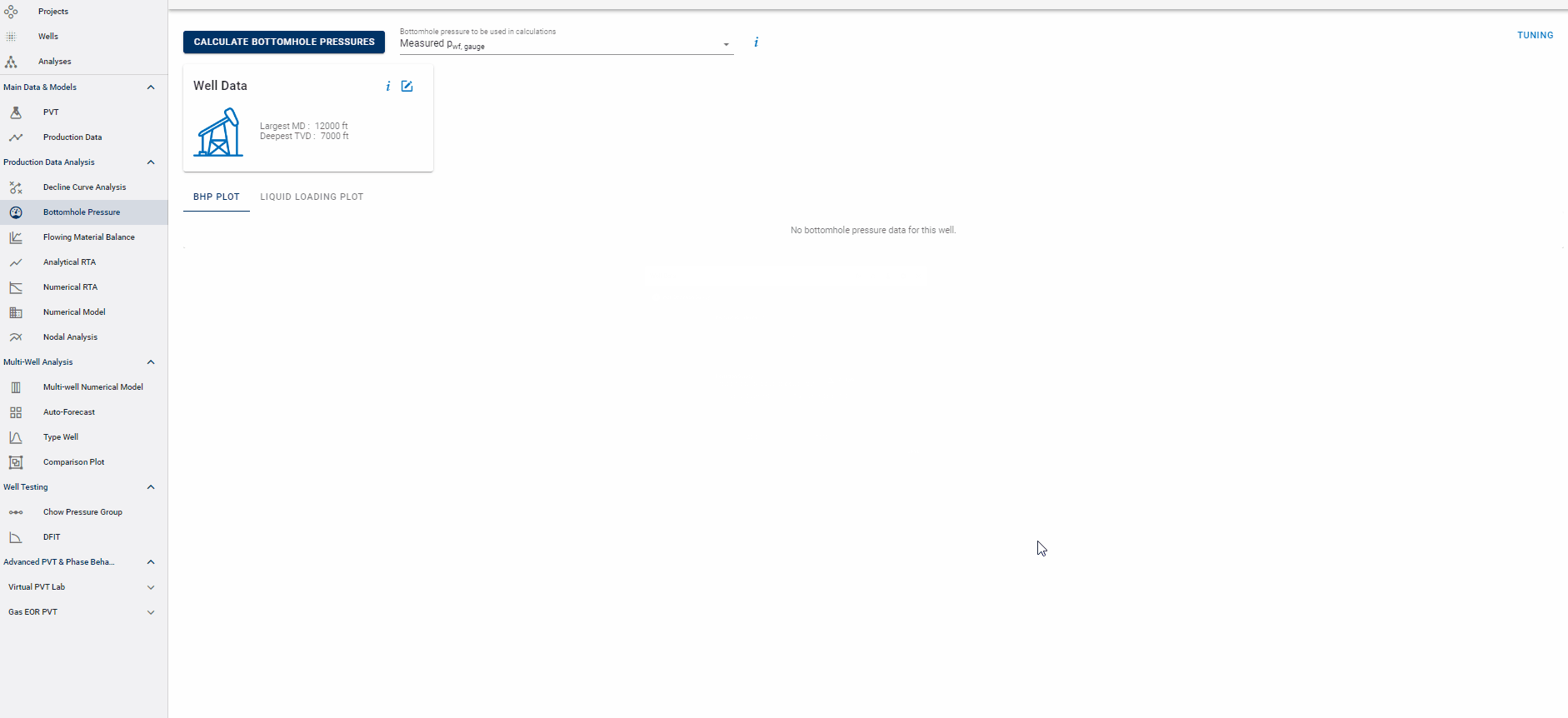
4. To adjust the fluid density in SWD wells is done through water salinity in Water PVT & Viscosity:

   
   

5. Numerical Model: History Matching

   a. In Well & Reservoir Data Card select “Well Type: Vertical, Radial” and input the reservoir properties:

   
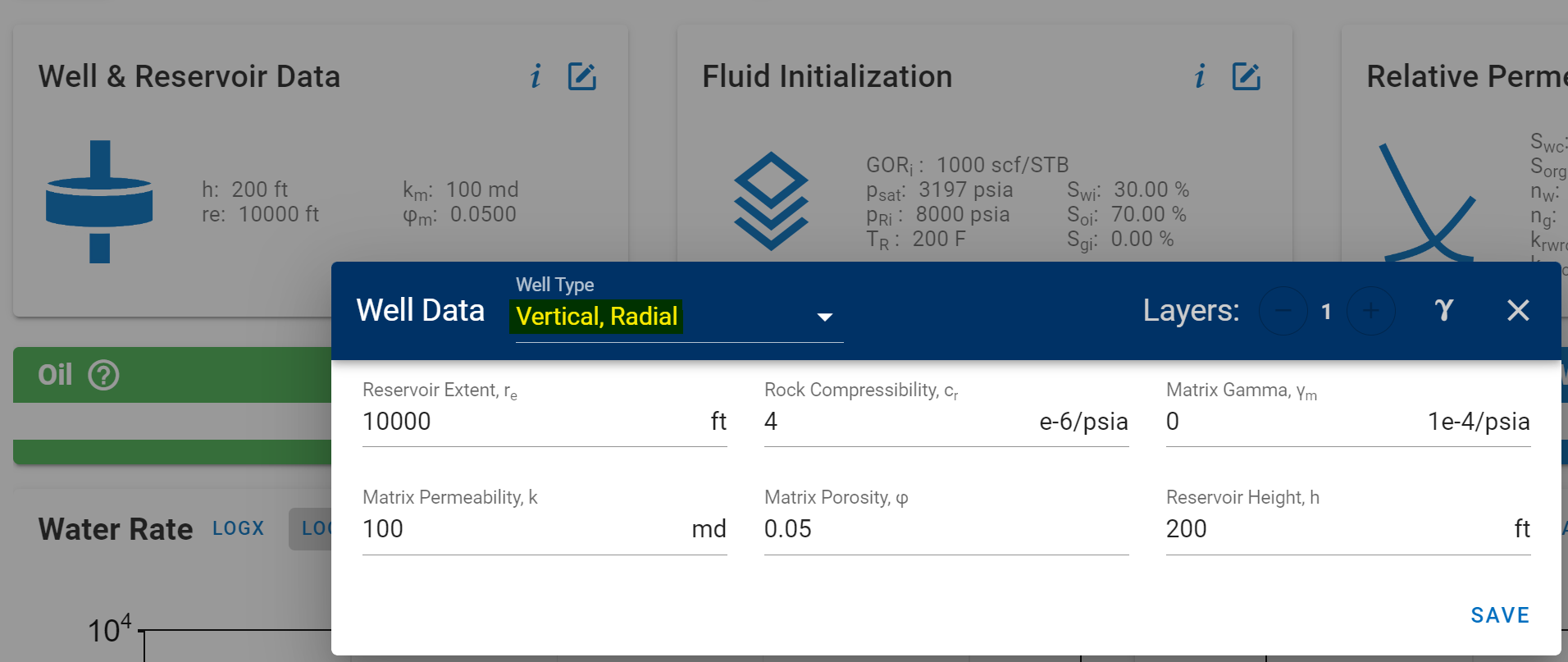
   Fig. 11: Radial Vertical Well

   b. Set well control to "Water Injection":

   
   Fig. 12: Water Injection Control

   c. Run the numerical model, compare the historical data with the simulated results.

   
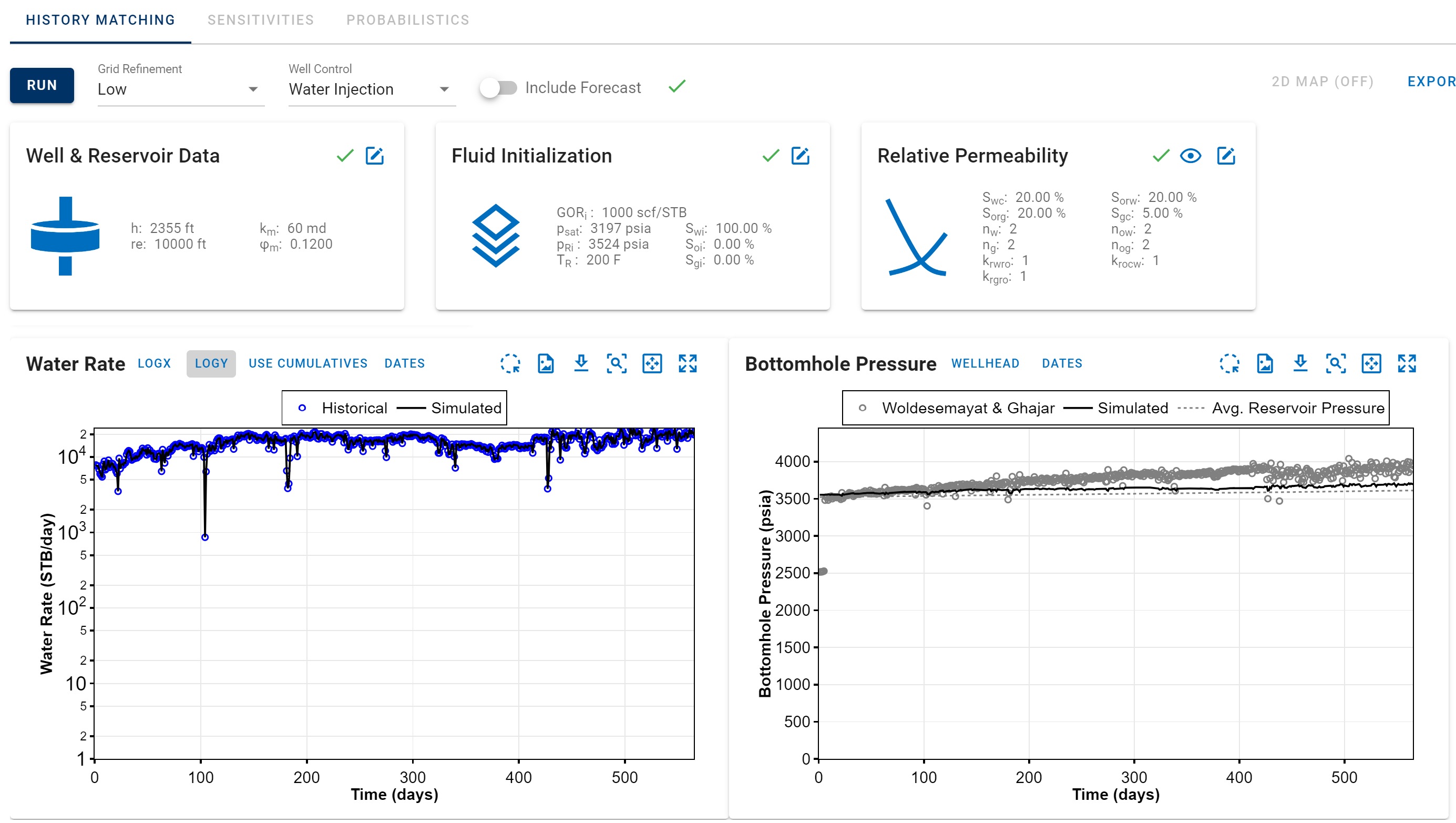
   Fig. 13: Numerical Model results

   d. Adjust the reservoir properties and any other relevant data as needed to achieve the desired bottomhole pressure.

   
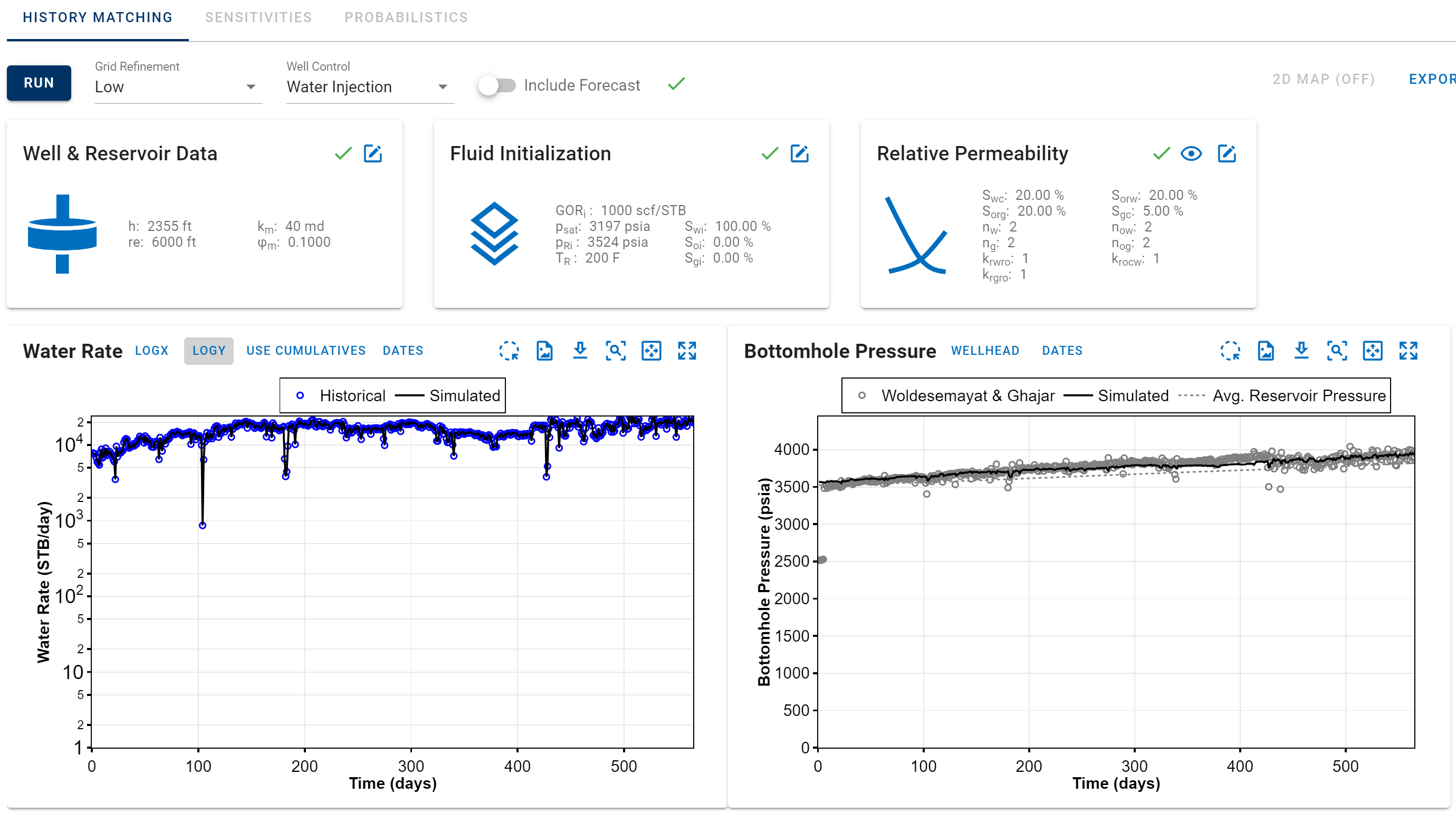
   Fig. 14: History Matching of Bottomhole Pressure

6. Numerical Model: Forecast

   a. Toggle on “Include Forecast”

   
   Fig. 15: Include Forecast

   b. Edit Forecast Schedule

   
   Fig. 16: Edit Forecast Schedule

   c. Set Forecast Options: Forecast type, initial forecast water and the constraint. And set the Forecast Profile: Forecast end time, constant water.

   
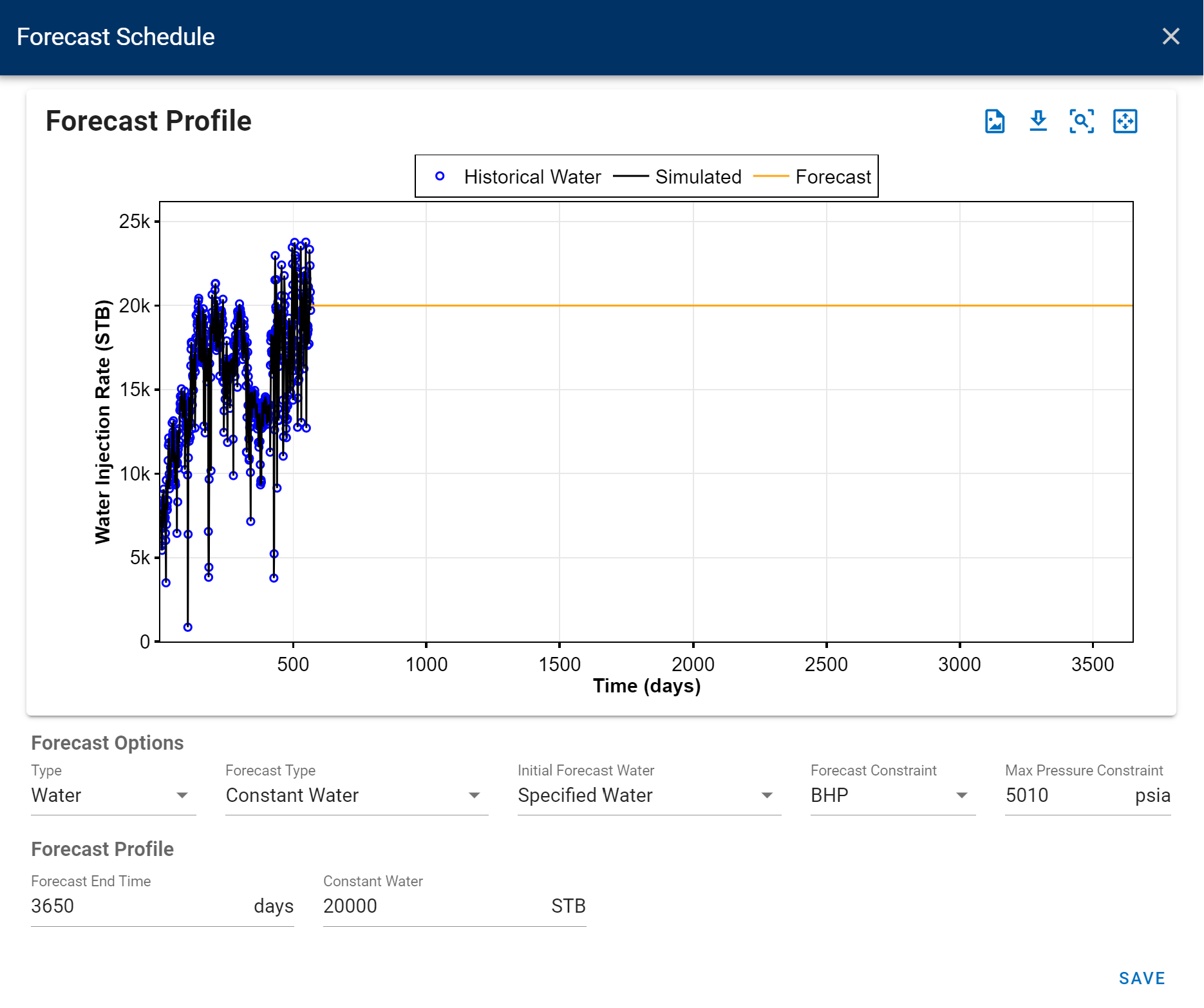
   Fig. 17: Forecast Schedule

   d. Run the simulation.

   
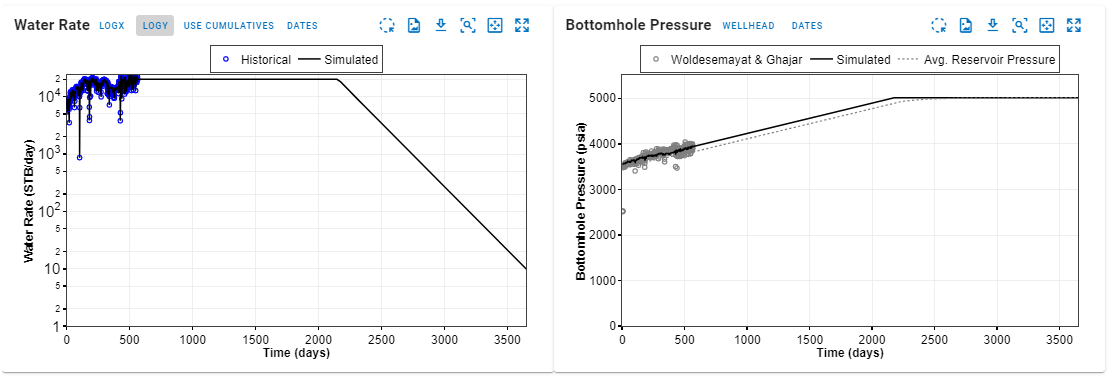
   Fig. 18: Forecast Results

9. Export Results and Other Options

To date, the production forecast results can be exported in excel format in daily or monthly option, while the dataset can be exported into:

1. OPM Flow
2. Eclipse (E100)

Let us know, if you'd like us to add another export option for your company. Contact us or use the Send Feedback button at the top right of whitson+.

9.1 Experimental Features

Apart from these exports to Excel, etc., this section also contains the following set of options to export simulated results to update the production data table in whitson⁺.

1. Set Hist. Data = Sim. Data: Updates the entire production data table for the well on whiston⁺ to replace the actual production rates and pressures with the simulated rates and pressures from the model. Note that the simulated rates and pressures will now replace the actual data here, so the real field production data (if it exists) will be lost.

   
   

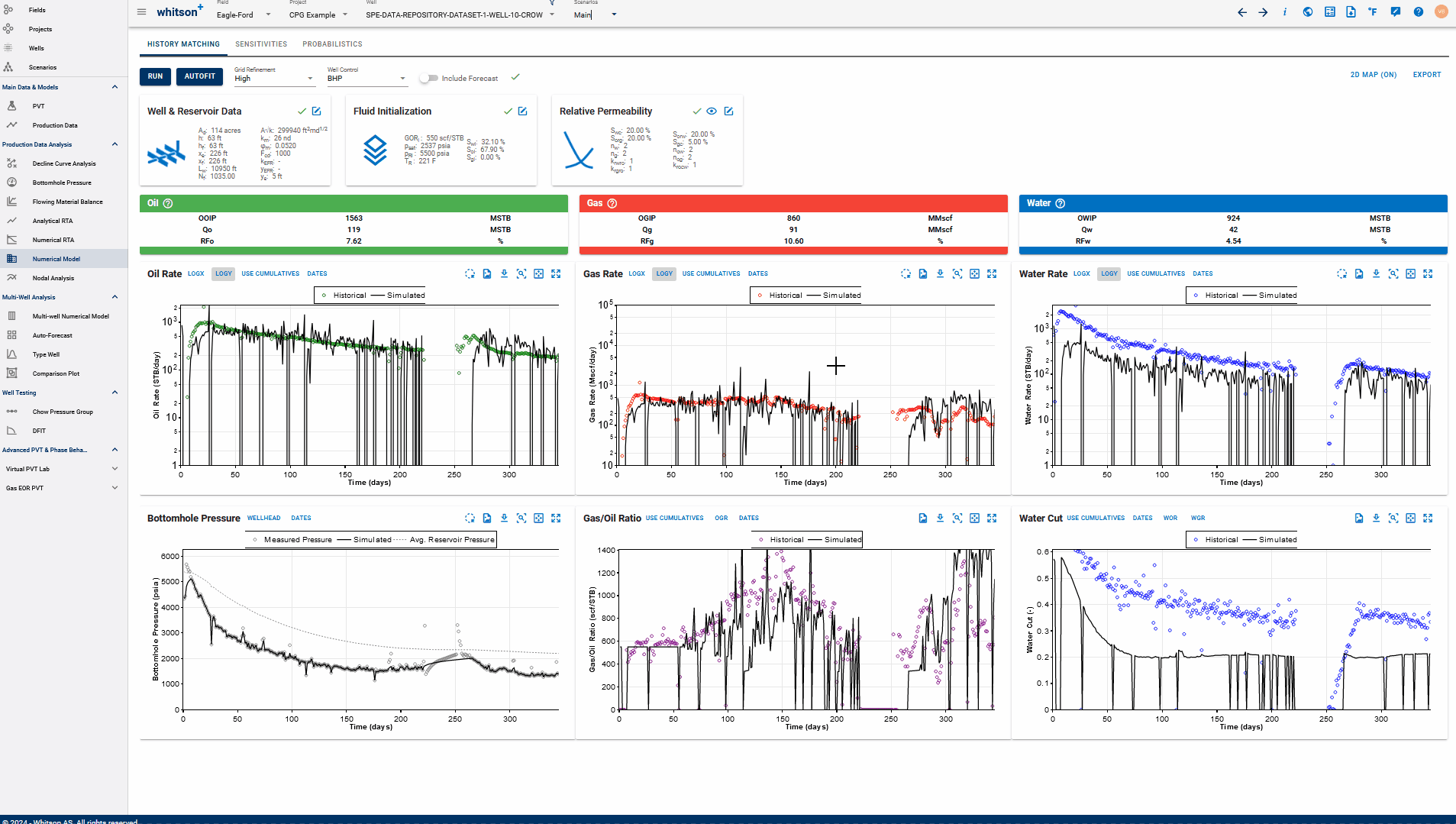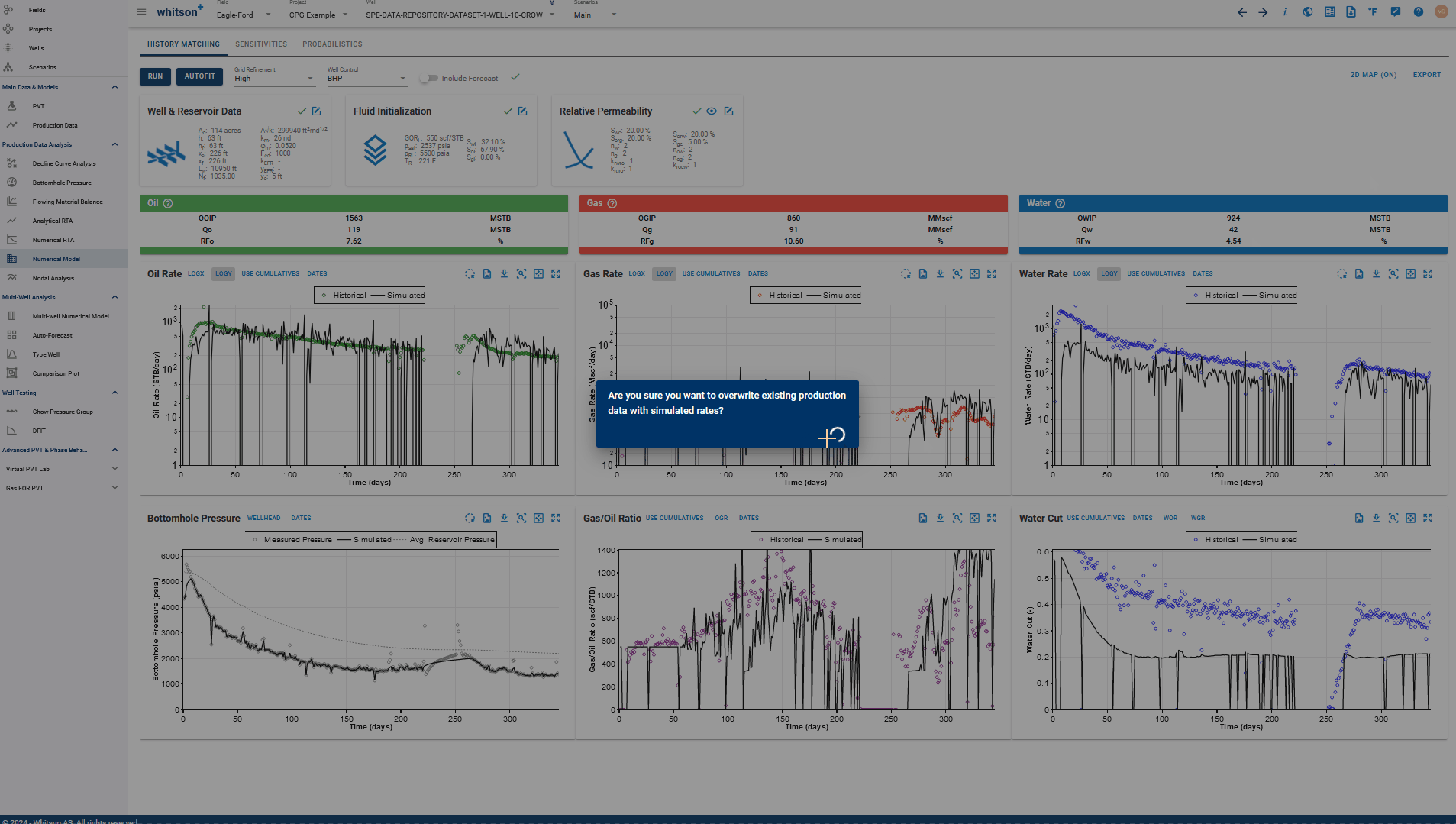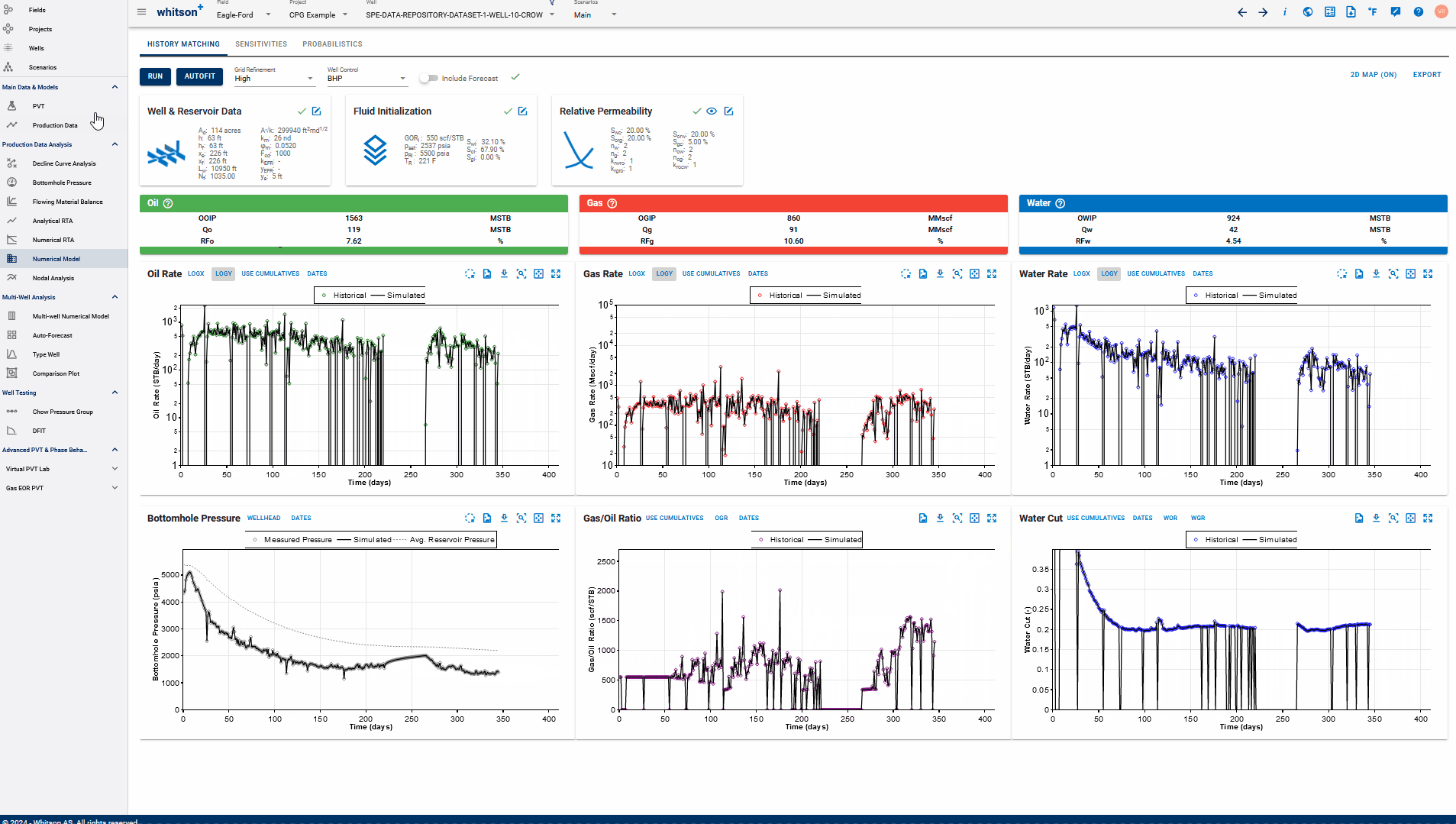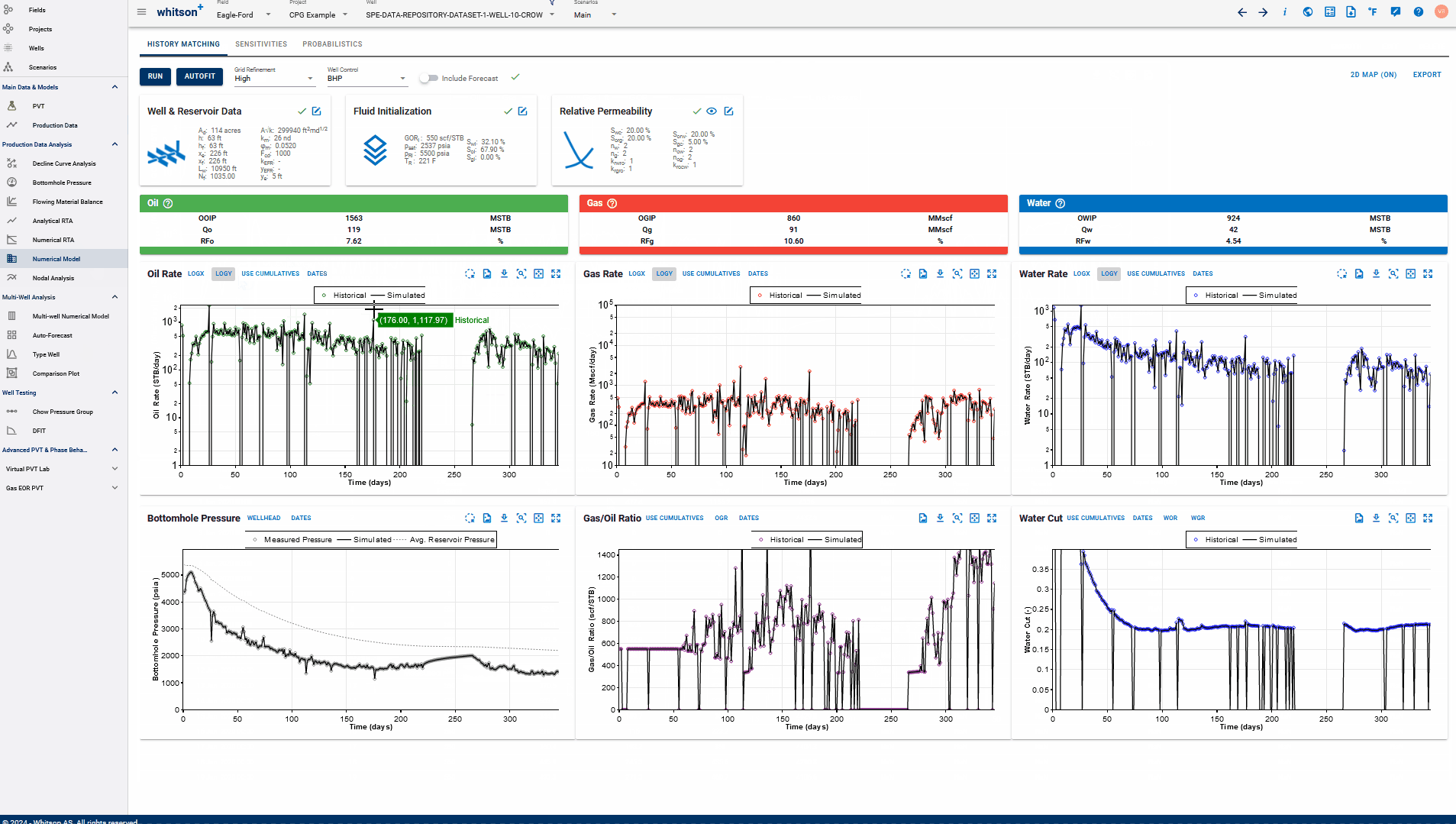
2. Set Hist. BHP = Sim. BHP: Updates only the gauge pressure in the production data table to be replaced with the BHP simulated output from the numerical model - does not replace any rates.

   
   

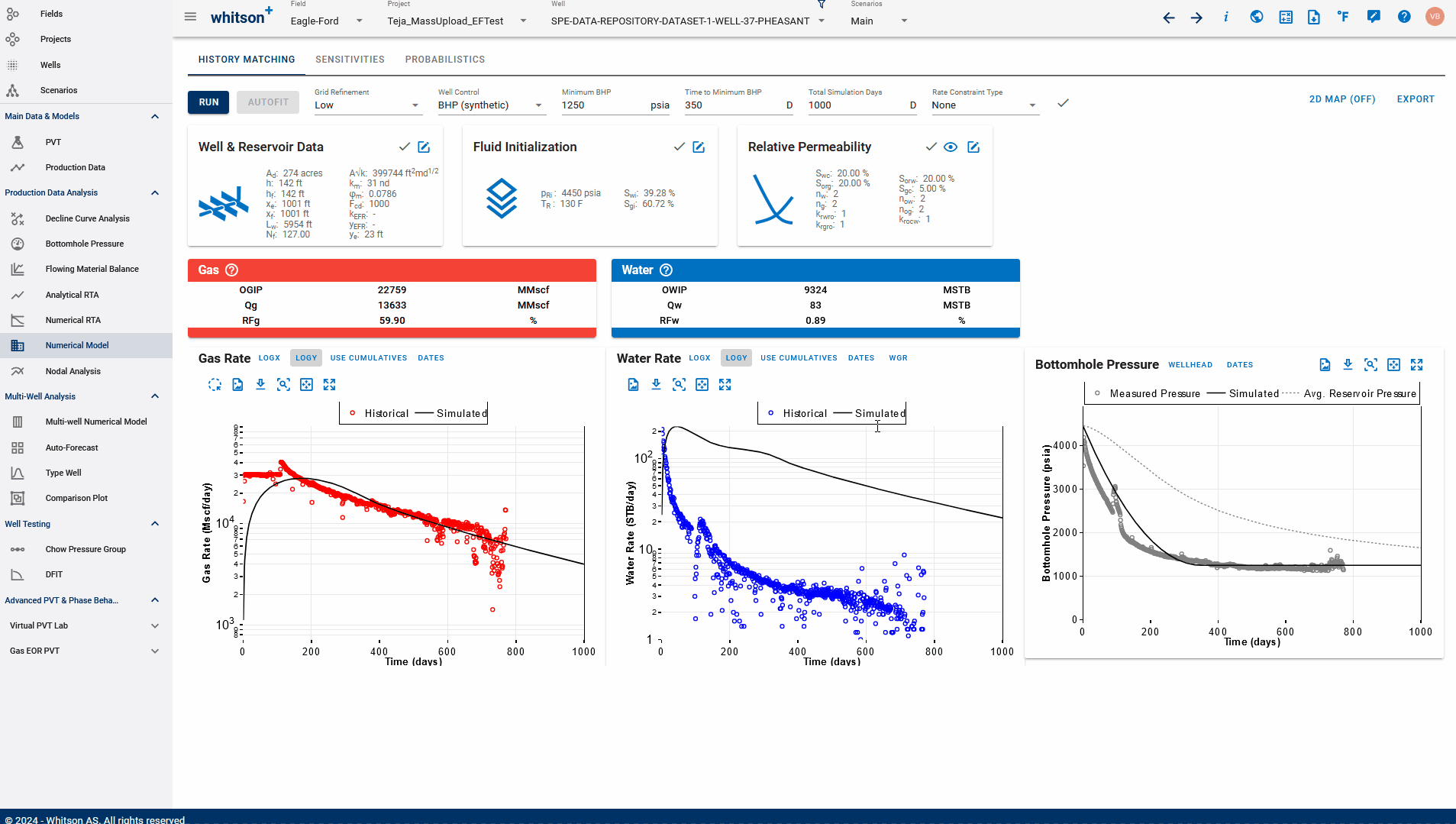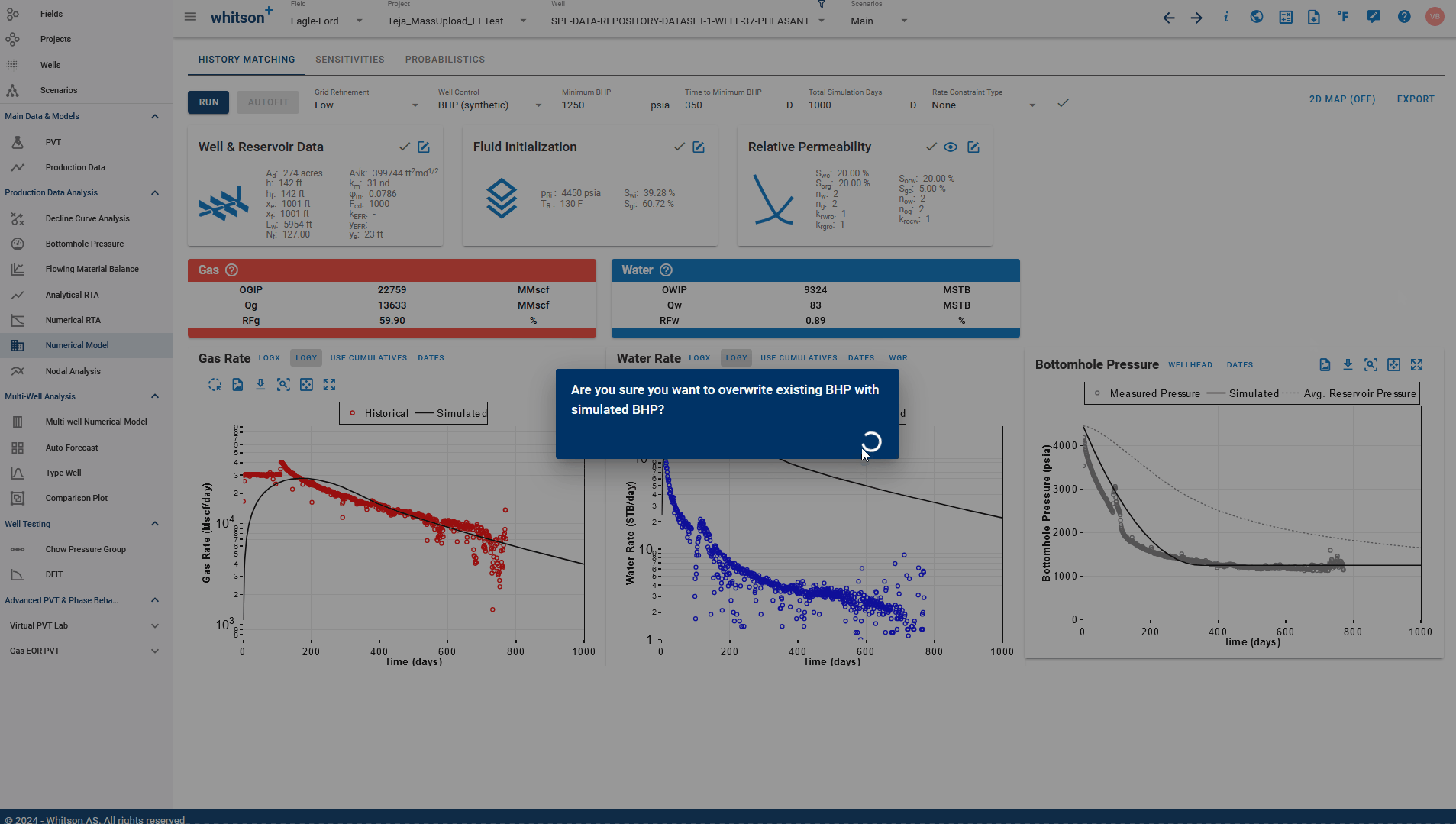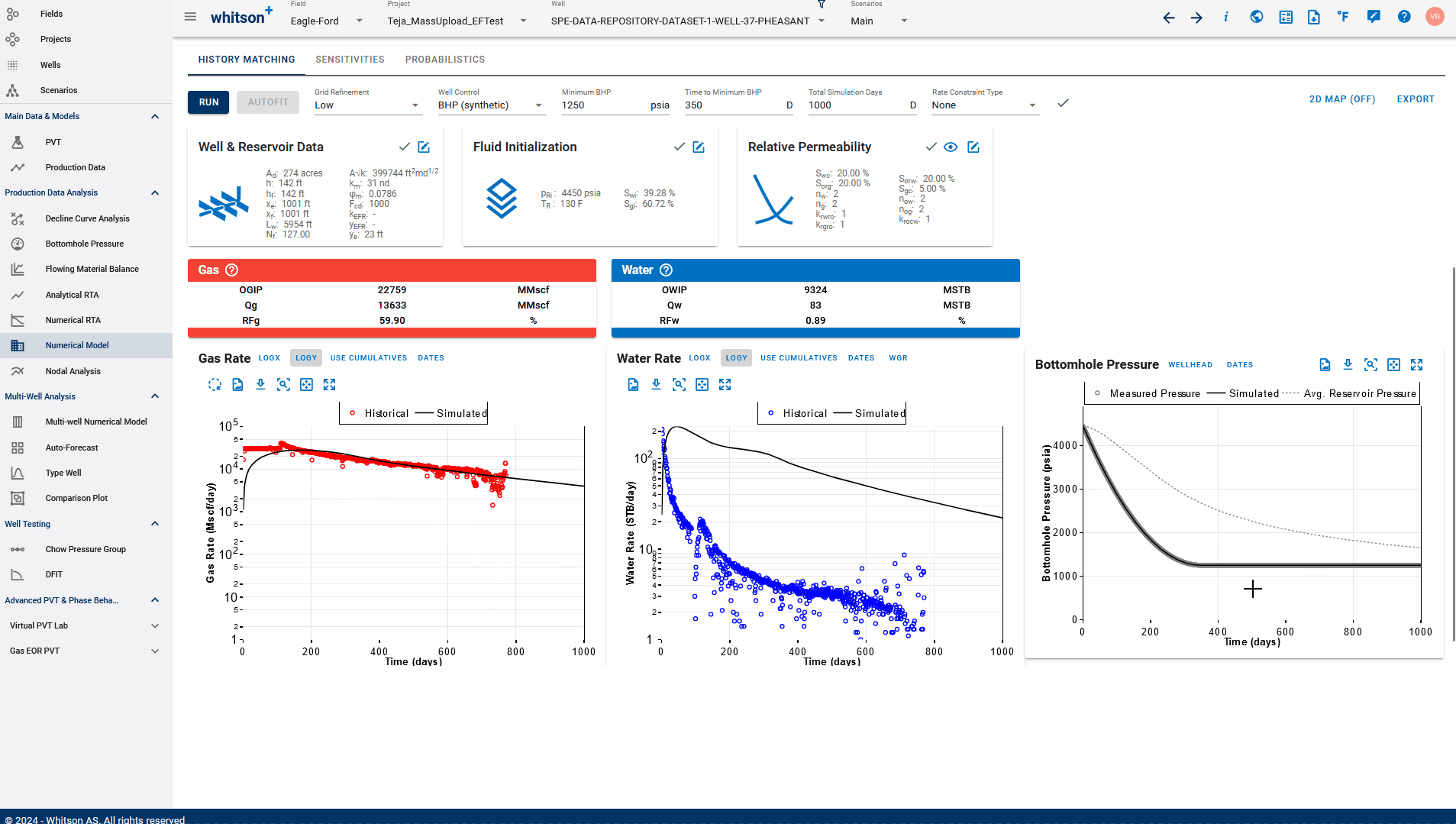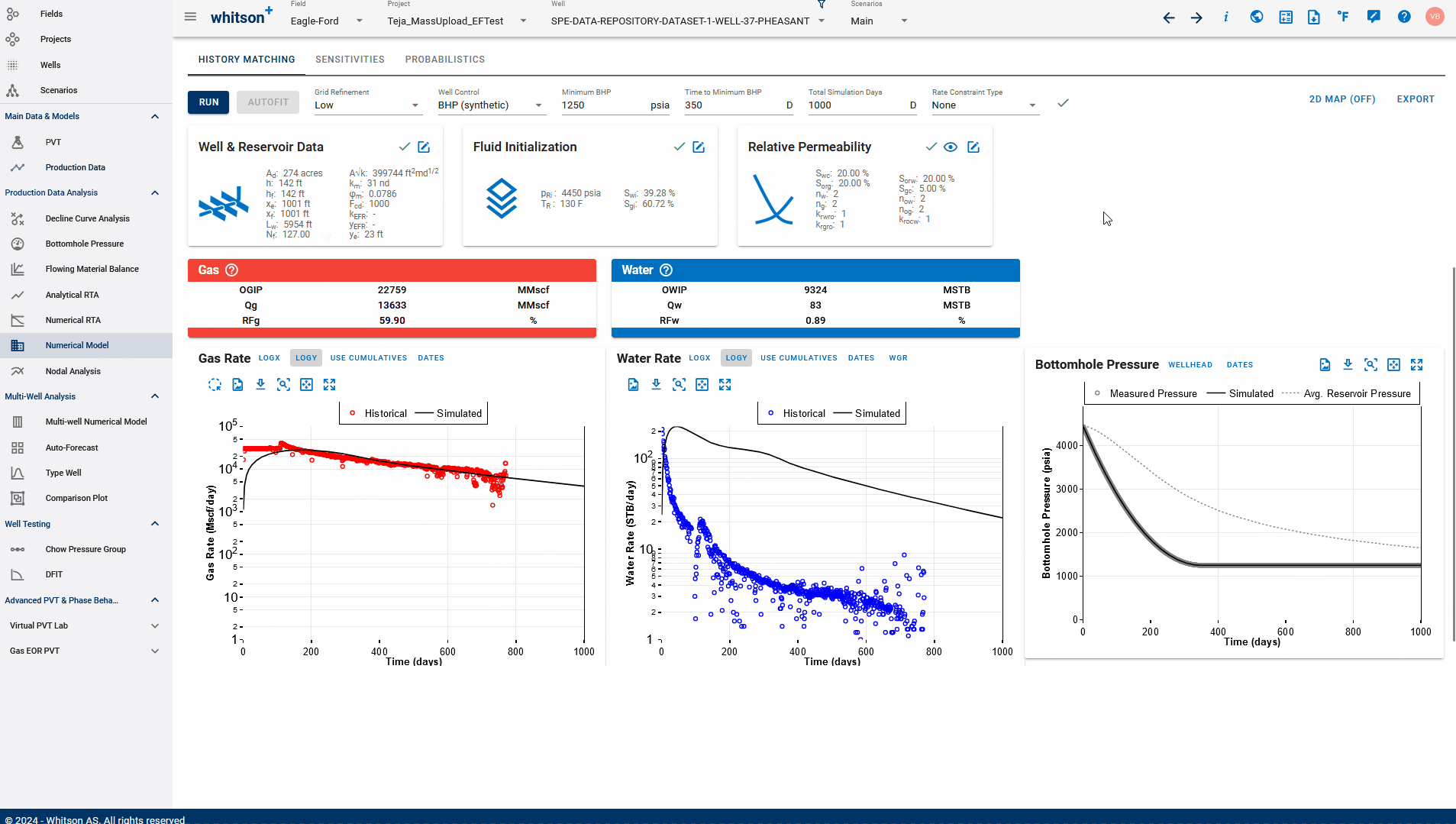
You can even build models first for synthetic wells without any production data, generate simulated output using BHP(synthetic) as well control, and use these options to generate a synthetic production data table, that is still true to the model, given the drawdown. These can be used to build and verify mental models of depletion, flow regimes, what-if analysis for drawdown scenarios and comparison.

9.1.1 Creating Synthetic Wells

Here's a GIF to show you how you can use these features quickly create a synthetic well and use the simulated data with the other features in whitson⁺ to test them on a simulated reservoir response-

10. Producing GOR in Multifractured Horizontal Wells

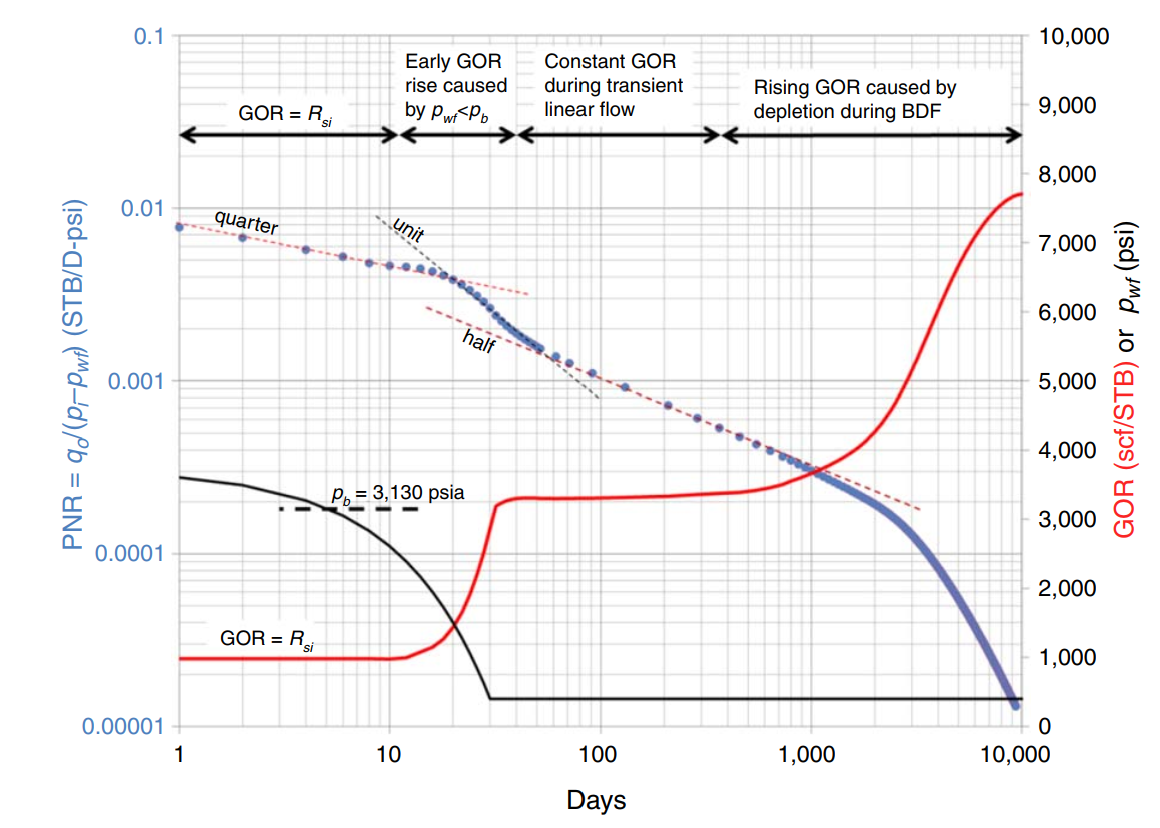
Horizontal wells with hydraulic fractures in tight oil reservoirs how producing GOR behavior that is very different from conventional, higher-permeability reservoirs (Steve Jones, 2016). Observed GOR behavior in tight black-oil reservoirs can be modelled after the following idealized stages throughout history. Some stages might not be visible becuase of the degree of undersaturation, flowing bottomhole pressure schedule, finite conductivity fractures and duration of infinite acting flow period. The stages are

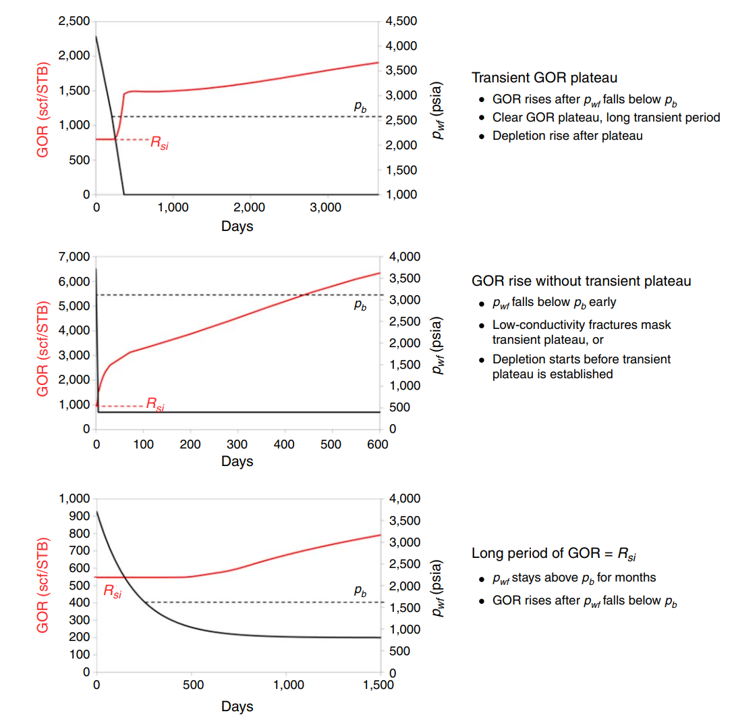
• Stage 1: Early GOR is constant at the initial solution GOR (Rsi) while bottomhole flowing pressure is above the bubblepoint.
• Stage 2: A rise in GOR as bottomhole flowing pressure declines to les than the bubblepoint.
• Stage 3: Transient GOR "plateau", which is characteristic of infinite acting (transient) linear flow.
• Stage 4: A continous rise in GOR during boundary-dominated flow (BDF).

Fundamental differences between infinite acting (IA) flow and boundary dominated flow (BDF), and the associated dependence of GOR on flowing bottomhole pressure, are important to understand. During IA (transient) linear flow, the GOR response changes in flowing bottomhole pressure is independent of the permeabilty for infinite-conductivity fractures, but not for finite-conductivity fractures.

Practical observations are;

• Knowing Rsi and the trasnient-GOR-plateau level in an areac an help one interpret where a well is in its GOR history.
• Classical RTA diagnostic plots are altered by rising GOR, and sometimes show an early init slope.
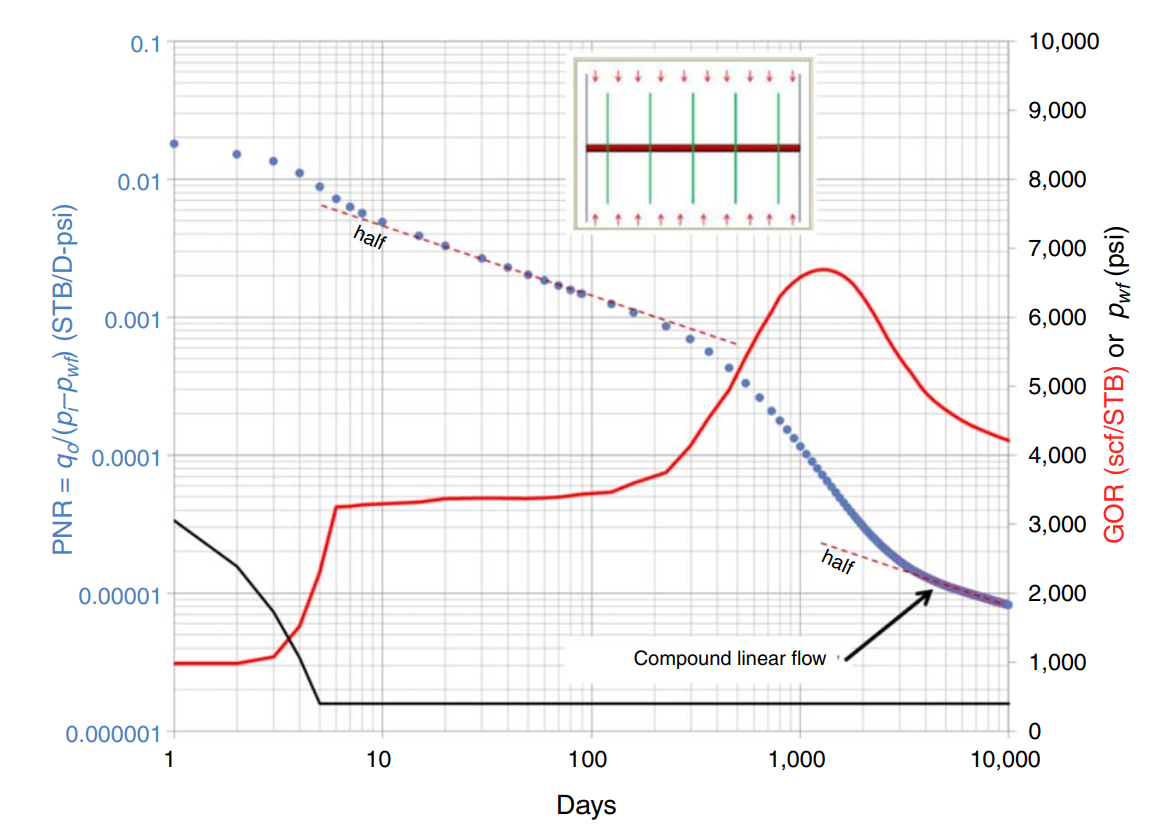
• During boundary-dominated flow, GOR is more a function of cumulative production than of time, but also recover oil more quikcly.
• If compound linear flow develops, GOR can decline late in the well life.

References

[1] Ray J. Ambrose, Robert C. Hartman, Yucel Akkutlu, Multi-Component Sorbed-Phase Considerations for Shale Gas-In-Place Calculations, SPE-141416, Society of Petroluem Engineers 2011

[2] Open Porous Media. 2023. OPM Flow Reference Manual, Version 2023-04. Oslo, Norway: OPM.

[3] S. Jones, Producing Gas-Oil Ratio Behavior of Multi-Fractured Horizontal Wells in Tight Oil Reservoirs, SPE-184397-PA. 2016