Adsorption

Shale reservoirs possess a remarkable capacity to store methane through a process known as "adsorption." This involves gas molecules adhering to the organic material within the shale, creating a near-liquid state of condensed gas. A useful analogy is to envision a magnet sticking to a metal surface or lint clinging to a sweater, illustrating the concept of adsorption versus absorption, where one substance is trapped inside another like a sponge soaking up water. The adsorption process is reversible due to its reliance on weak attraction forces.

Compared to conventional reservoirs, shale reservoirs can store significantly more gas in the adsorbed state, even when compression is applied at pressures below 1000 psia. Notably, the gas stored in shale is predominantly held in the adsorbed state, as opposed to being free gas. This is because the volume of the cleat or fracture system within shale is relatively small compared to the overall reservoir volume. As a result, the pressure volume relationship is commonly described through the desorption isotherm alone.

Langmuir Isotherm

The release of adsorbed gas is commonly described by a pressure relationship called the Langmuir isotherm. The Langmuir adsorption isotherm assumes that the gas attaches to the surface of the shale, and covers the surface as a single layer of gas (a monolayer). At low pressures, this dense state allows greater volumes to be stored by sorption than is possible by compression.

The typical formulation of the Langmuir isotherm is:

$$\begin{equation} \label{eq:langmuir} c_g = \frac{V_{LS}p}{p_{LS}+p} \end{equation}$$

Langmuir Volume, V_LS

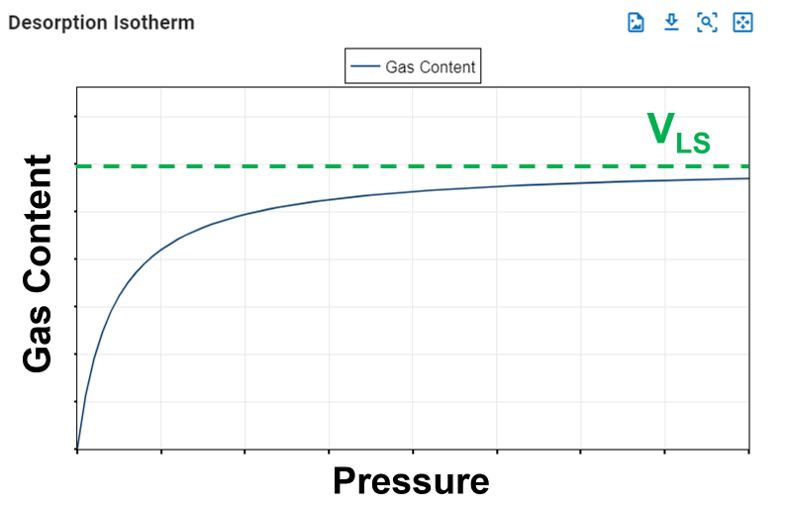
The Langmuir volume is the maximum amount of gas that can be adsorbed by a shale at a "infinite pressure". The plot below of a Langmuir isotherm demonstrates that gas content asymptotically approaches the Langmuir volume as pressure increases to infinity.

Fig. 1: Langmuir Volume

Langmuir Pressure, p_LS

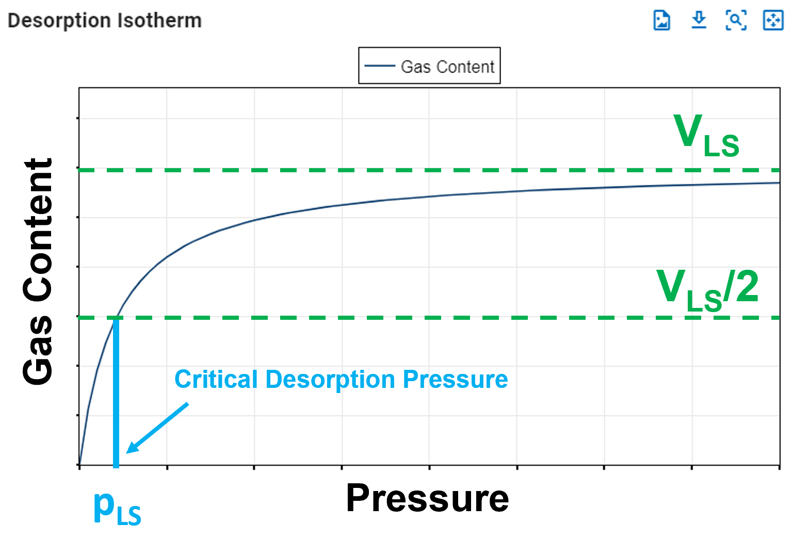
The Langmuir pressure, or critical desorption pressure, is the pressure at which one half of the Langmuir volume can be adsorbed. As seen in the figure below, it changes the curvature of the line and thus affects the shape of the isotherm.

Fig. 2: Langmuir Pressure

Computing Original Gas in Place (OGIP)

Ambrose et al.[1] argue that the free (OGIP) must be corrected for the adsorbed gas that occupies some of the hydrocarbon pore volume (HCPV). If porosity is estimated from core plugs where core preparation has removed the adsorbed gas, then the OGIP will be overestimated.

The convention of reporting OGIP when adsorption is included, is to report it in units of scf/ton (standard cubic feet per short ton). For a fluid system having only dry/wet gas and water, the total OGIP is

$$\begin{equation} \hat{G}=\hat{G}_{f} + \hat{G}_a \end{equation}$$ where

$$\begin{align} \label{eq:freegasperton} \hat{G}_f &= C_1 \frac{\phi(1-S_{wi})-\phi_a}{\rho_bB_{gd}}\\ \label{eq:adsorbedgasperton} \hat{G}_a &= V_{SL} \frac{p}{p+p_{SL}} \end{align}$$ and $$\begin{equation} \phi_a = C_2 M_g \frac{\rho_b}{\rho_s}\bigg(V_{LS}\frac{p}{p+p_{LS}}\bigg) \end{equation}$$ with \(C_1\approx 5.7060\) and \(C_2\approx1.318\cdot10^{-6}\) are unit conversion factors. The shale saturation is capped at \(1-S_{wi}\), meaning the maximum amount of shale you can have is the entire HCPV. Hence, this will make the results independent of the adsorption numbers when violating this constraint.

The OGIP resolved in the ARTA and GFMB features yields the free OGIP. We can use this volume to compute the rock mass, which in turn can be used to calculate the adsorbed OGIP. Multiplying equation \eqref{eq:freegasperton} with the rock mass (\(G=\hat{G}_f m_r\)) gives the free OGIP in units of scf. Solving for the rock mass yields

$$\begin{equation} m_r = \frac{G_f}{C_1} \frac{\rho_b B_{gd}}{\phi(1-S_w)-\phi_a} \end{equation}$$

This rock mass can then be multiplied by equation \eqref{eq:adsorbedgasperton} to get the adsorbed OGIP in scf, i.e., $$\begin{equation} G_a =\hat{G}_a m_r = V_{SL} \frac{p}{p+p_{SL}} m_r \end{equation}$$

Total Compressibility when Adsorption is ON

In order to honor mass balance, it becomes necessary to modify total system compressibility when accounting for adsorption. Total system compressibility can be determined using the following equation:

$$\begin{equation} c_t = c_f + \left(1-S_{wc}\right)c_g + S_wc_w+\frac{\rho_b\rho_g^{sc}}{2000\phi\rho_{ga}}\frac{V_Lp}{p+p_L}\left[\left(\frac{62.428\rho_{ga}}{1000\rho_g^{sc}}B_g-1\right) \left(c_f+\frac{p_L}{p\left(p+p_L\right)}\right)-c_g\right] \end{equation}$$

The derivation of this equation is shown here and is contructed upon Ambrose et al.[1].