Classical RTA

1. Theory

There have been many studies showing that infinite acting, linear flow is the dominant flow regime in multifractured horizontal wells for tight unconventional reservoirs. Most common production analysis of linear flow was first introduced by Wattenbarger et al. in 1998. They proposed analytical solutions for both constant rate and constant pressure. In reality, rates and pressures are changing simultaneously. To account for that, the principle of superposition is applied.

In 1993, Palacio and Blasingame (1993) introduced the concept of material balance time (MBT). Material balance time

• is a superposition time function.
• converts variable rate data into an equivalent constant rate solution.
• is rigorous for a boundary dominated flow regime
• works well for transient data also, but is only an approximation (errors can be up to 20% for linear flow)

In the whitson+ classical RTA module, material balance time is the default time function, hence the theory for the constant rate solution is emphasized in this part of the manual. On the other hand, there is an option to use constant pressure solution by selecting "Real Time" as a function of time as presented here.

The purpose of conducting this analysis is to determine the linear flow parameters (LFP=\(A\sqrt{k}\)) and drainage volume by interpreting production data. By using Arps equation with respect to time to end of linear flow \((t_{elf})\), production forecast can be made.

1.1 Assumptions

Fig. 1: Wellbox model

Fig.1 shows the geometry of the well used as a base assumption of these analyses. The fracture is assumed to have infinite fracture conductivity, such that the linear flow is perpendicular to the fracture. Additionally, this module assumes single-phase flow with no flow beyond the fracture tip (\(x_e=x_f\) and \(h=h_f\)), i.e. a fully-penetrating fracture (1D-model).

1.2 Superposition Time

There are two superposition time function options in whitson⁺; material balance time and linear superposition time. In addition to these, one can use real time (called "Variable Pressure" in other tools), in which no superposition time function has been applied.

1.2.1 Material Balance Time - DEFAULT

The use of material balance time is common in the rate transient analysis, and is the default in whitson⁺. Material balance time

• is a superposition time function.
• converts variable rate data into an equivalent constant rate solution.
• is rigorous for a boundary dominated flow regime
• works well for transient data also, but is only an approximation (errors can be up to 20% for linear flow)

Mathematically, material balance time, MBT \((t_c)\) is expressed in: $$\begin{equation} \label{MBT} t_c=\frac{Q(t)}{q(t)} \end{equation}$$

where \(Q(t)\) and \(q(t)\) are cumulative production and production rate at time \(t\).

1.2.2 Linear Superposition Time

Mathematically, linear superposition time, \((t_{\text{linear}})\) is expressed as:

$$\begin{equation} \label{linear_superposition_time} t_{\text{linear}} = \left( \sum_{j=1}^{n} \frac{q_j - q_{j-1}}{q_n} \cdot \sqrt{t - t_{j-1}} \right)^2 \end{equation}$$

1.3 Phase

You can select to run the classical RTA analysis with either of the following rates

• Oil (Surface)
• Gas (Surface)
• Hydrocarbon (Reservoir)
• Liquid (Reservoir)
• Total (Reservoir)

Hydrocarbon reservoir rates are calculated from surface rates using PVT and bottomhole pressures as follows

$$\begin{equation} \label{eq:hc_rate} q_{hc} = q_{o,res} + q_{g,res} \end{equation}$$

Liquid reservoir rates are calculated from surface rates using PVT and bottomhole pressures as follows

$$\begin{equation} \label{eq:liq_rate} q_{liq} = q_{o,res} + q_{w,res} \end{equation}$$

Total reservoir rates are calculated from surface rates using PVT and bottomhole pressures as follows

$$\begin{equation} \label{eq:tot_rate} q_{tot} = q_{o,res} + q_{g,res} + q_{w,res} \end{equation}$$

In which \(q_{g,res}\), \(q_{g,res}\) and \(q_{w,res}\) can be calculated as follows

$$\begin{equation} \label{eq:res_gas} q_{g,res} = \frac{q_g-R_sq_o}{1-R_sr_s}B_{gd} \end{equation}$$

$$\begin{equation} \label{eq:res_oil} q_{o,res} = (q_o-\frac{q_{g,res}}{B_{gd}/r_s})B_o \end{equation}$$

$$\begin{equation} \label{eq:res_water} q_{w,res} = q_wB_w \end{equation}$$

The PVT properties solution GOR, \(R_{s}\), oil formation volume factor, \(B_{o}\), solution CGR, \(r_{s}\), gas formation volume factor, \(B_{gd}\), and water formation volume factor, \(B_{w}\) is all evaluated at the flowing bottomhole pressure, \(p_{wf}\), every given day to calculate total rates.

If Gas (Surface) are used for liquid-rich systems (oil rate, \(q_{o,sc}\), larger than 0), the oil rate is added as an equivalent gas volume using this formula

$$\begin{equation} \label{eq:wet_gas_rate} q_{g,wet} = q_{g,sc} + q_{o,sc}C_{og} \end{equation}$$

where \(C_{og}\) is a conversion from surace-oil volume in STB to an "equivalent" surface gas in scf

$$\begin{equation} \label{eq:cog} C_{og} = 133,000 \frac{\gamma_{og}}{M_{og}} [scf/STB] \end{equation}$$

the \(M_{og}\) is estimated with the Cragoe correlation

$$\begin{equation} \label{eq:cragoe} M_{og} = \frac{6,084}{\gamma_{api}-5.9} \end{equation}$$

This rate, \(q_{g,wet}\), is typically referred to as a "wet" or "fat" gas rate.

1.4 Rate Normalized Pressure (RNP)

Rate Normalized Pressure (RNP) is very useful for production analysis where flowing pressures and rates change through time. It is defined as the flowing pressure drop divided by rate.

$$\begin{equation} \label{eq:RNP} RNP = \frac{\Delta p}{q} = \frac{p_i-p_{wf}}{q} \end{equation}$$

1.5 Pressure Normalized Rate (PNR)

Pressure normalized rate is the inverse of rate normalized pressure. Pressure normalized rate is very useful for production analysis where flowing pressures and rates change through time. It is defined as the rate divided by flowing pressure drop.

$$\begin{equation} \label{eq:PNR} PNR = \frac{q}{\Delta p}= \frac{q}{p_i-p_{wf}} \end{equation}$$

1.6 RTA Derivatives

Derivatives assists with flow regime identification and can be calculated for both pressure (p), rate normalized pressure (RNP) and pressure normalized rate (PNR).

Derivative analysis amplifies the reservoir signal, but also amplfies the noise. - Dave Anderson

1.6.1 Derivative Options

The logarithmic derivative used in RTA applied directly on the rate normalized pressure (RNP) data is given by, i.e., $$\begin{equation} RNP' = \frac{\delta RNP}{\delta log(t)} = t\frac{\delta RNP}{\delta t} \end{equation}$$ .

There are three different ways to compute this derivative in whitson⁺:

• The Bourdet Derivative (Bourdet et al., 1989)
• Weighted Central Difference
• Central Difference

1.6.2 Bourdet Derivative (RECOMMENDED)

The Bourdet derivative is commonly used in well-test analysis (PTA) for identifying flow regimes (Lee et al., 2003) and has similarly found utility in RTA.

Governing Equation

To calculate the Bourdet derivative (Bourdet et al., 1989) at any given point, one point before (left) and one point after (right) is used.

$$\begin{equation} RNP' = \frac{\frac{RNP_L}{\Delta ln(t)_L}\Delta ln(t)_R + \frac{RNP_R}{\Delta ln(t)_R}\Delta ln(t)_L}{\Delta ln(t)_L + \Delta ln(t)_R} \end{equation}$$

Smoothing

The Bourdet approach is illustrated in Fig. 2 and is a way to calculate and smooth the derivative based on a log-cycle window size, L.

Fig. 2: Illustration of a derivative calculating using the Bourdet method. Image courtesy of Samaneh Moghadam (April, 2020). Modified from Lee et al. (2003).

It is different from a weighted central difference in the way that it uses a constant log-cycle window size, L, on both sides of the point of derivation. A weighted central difference, on the other hand, uses a constant index step size, e.g. i-5 and i+5 for step size of 5, on each side of the point of derivation. The window size, L, represents the log-cycle fraction used to control the amount of smoothing. Typical values are 0.01 to 0.2. The default L in whitson⁺ is 0.2. The larger the L value, the more smoothing.

The Bourdet algorithm implemented in whitson⁺ was provided by Behnam Zanganeh.

1.6.3 Weighted Central Difference

The weighted central difference is given by,

$$\begin{equation} RNP' = \frac{\frac{RNP_L}{\Delta ln(t)_L}\Delta ln(t)_R + \frac{RNP_R}{\Delta ln(t)_R}\Delta ln(t)_L}{\Delta ln(t)_L + \Delta ln(t)_R} \end{equation}$$

where the \(L\)-subscript refers to the index to the left with a constant step size, \(S\), i.e. \(i-S\) and the \(R\)-subscript refers to the index to the right with a constant step size, \(S\), i.e. \(i+S\).

1.6.4 Central Difference

This is the naive implementation, given by three points per derivative for central difference in the following manner

$$\begin{equation} t\frac{RNP}{\delta t} = t_i\frac{RNP_{i+1}-RNP_{i-1}}{t_{i+1}-t_{i-1}} \end{equation}$$

1.6.5 Derivatives in Material Balance Time

Because of noise in real field data, material balance time may not be in sequence. This might cause problems in derivative calculations. Hence, the data must be sorted in terms of increasing material balance time prior to calculating the derivative. The following procedure, adapted from Samandarli et al.(2012), is used for this purpose.

1. RNP and material balance time \((t_c)\) are calculated at each real time step.
2. RNP and \((t_c)\) are sorted in increasing order of material balance time, with repeat material balance times eliminated.
3. The RNP derivative, RNP', is then calculated using the sorted data.

1.7 RTA Integrals

In the case of complex and noisy data, Blasingame et al. [1] introduced the concepts of pressure-integral and pressure-integral difference which have become essential tools in scrutiny of well-test data throught type-curve analysis. Similarly, McCray (1990) presented the idea of the rate-integral and rate-integral derivative which was utilized by Blasingame and his students and colleagues for type-curve analysis of production data in various publications.

1.7.1 The Rate Normalized Pressure (RNP) Integral

The use of integral of the RNP \(\left(IRNP\right)\) and its derivative \(\left(IRNP'_R\right)\) was suggested by Chu et al. [6] for the study of flow-regime signature in the Wolfcamp shale. For liquids, the equations are written as follows:

$$\begin{equation} \label{eq:RTA-integral} IRNP=\frac{1}{t_{MB}}\int_{0}^{t_{MB}}\frac{p_i-p_{wf}(\tau_{MB})}{q(\tau_{MB})}d(\tau_{MB}) \end{equation}$$

$$\begin{equation} \label{eq:RTA-integral-derivative} IRNP'_R = \frac{dIRNP}{dln(\tau_{MB})} \end{equation}$$

The integral can be calculated using various time functions (real time, linear superposition time). However, it is presented here in material balance time for example purposes.

As with \(\left(RNP\right)\) and \(\left(RNP'_R\right)\) the calculations for \(\left(IRNP\right)\) and \(\left(IRNP'_R\right)\) can be applied to gases through inclusion of gas pseudovariables.

1.7.2 Discrete Calculation

The discrete form of Eq. \eqref{eq:RTA-integral} is expressed in the following manner: $$\begin{equation} \label{eq:RTA-integral-discrete-form} IRNP=\frac{1}{t}\sum_{i=1}^{n}\left(\frac{RNP\left(t_i\right)+RNP\left(t_{i-1}\right)}{2}\right)\left(t_i-t_{i-1}\right) \end{equation}$$

1.7.3 LFP (A√k) Adjustments

The conversion from a slope to LFP (A√k) while using the RNP integral must be adjusted by 2/3 to ensure that the LFP is calculated correctly from the slope. This follows from integrating the RNP as a function of √t.

$$\begin{equation} RNP = mt^{1/2} + b \end{equation}$$

$$\begin{equation} \int RNP \, dt = \frac{2}{3}mt^{3/2} + bt \end{equation}$$

$$\begin{equation} \frac{\int RNP \, dt}{t} = \frac{2}{3}mt^{1/2} + b \end{equation}$$

When turning on the integral function, this correction is applied

1.8 Flow Regimes

The Pressure Normalized Rate plot (log-log plot of PNR vs t) can be used as a diagnostic plot to identify the flow regimes in different portions of the well data (early, middle and late time). The flow regimes represent the way the fluid flows into the wellbore, often a function of shape and size of the reservoir, well completion, and duration of flow. Each flow regime is identified by the data showing a characteristic slope on this log-log plot.

whitson⁺ offers the ability to add 3 different interpretation lines using the '/' button on the PNR plot. These lines are aligned with the data for interpreting the flow regime and can be broadly associated with the following -

Interpretation Line	Slope Value	Flow Regime
Quarter Slope	-1/4	Bilinear Flow (low Fcd wells)
Half slope	-1/2	Infinite Acting Linear Flow - typical in MFHW
Unit slope	-1	Pseudosteady State, Boundary Dominated Flow

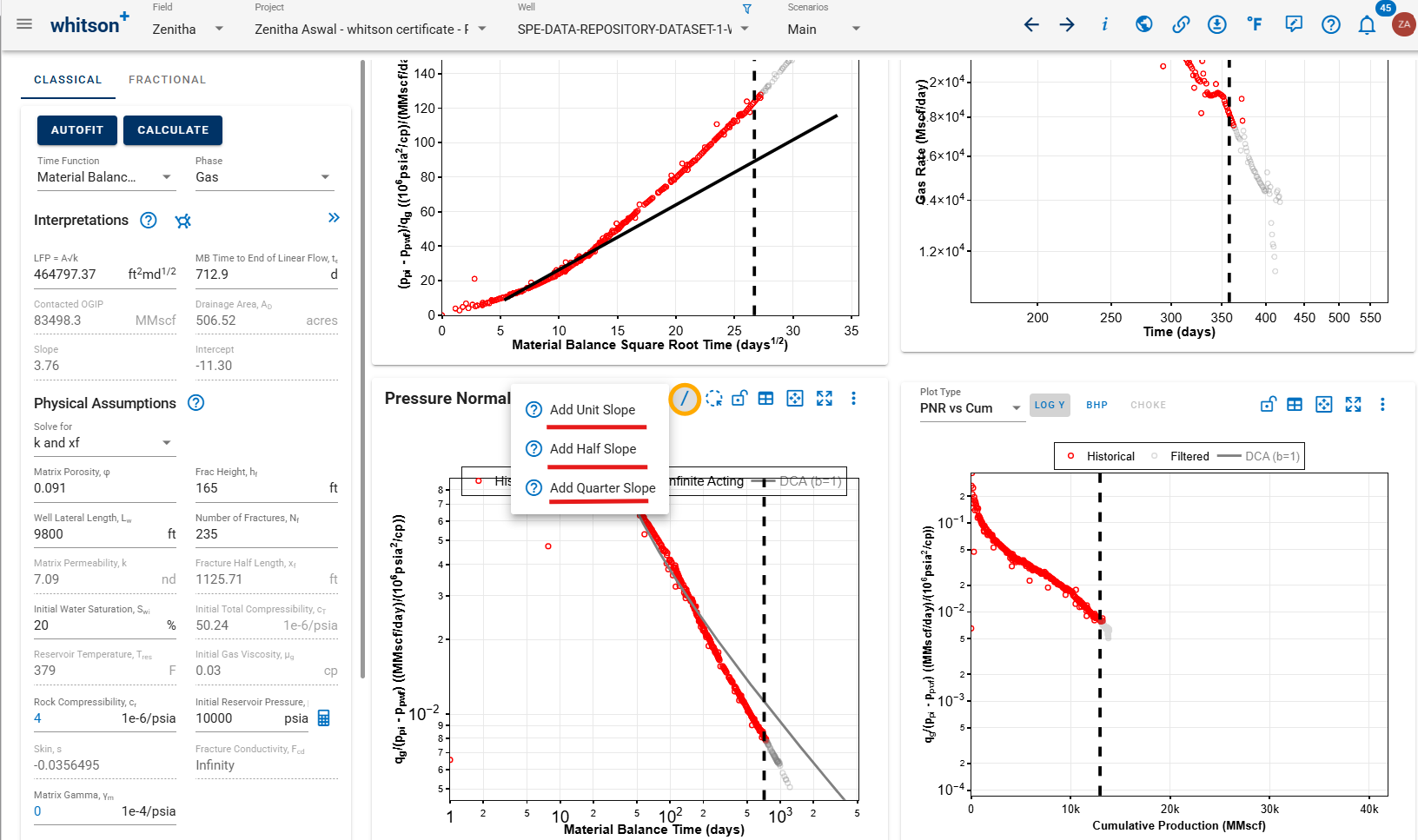
Interpretation of flow regimes can be highly subjective since these flow regimes do not have sharp transitions and may present long transient periods between them - especially in low permeability, unconventional reservoirs and multi-fractured horizontal wells (MFHW). It is also important to be aware of the time scale and order of the interpretation when identifying flow regimes. For example, a unit slope at early time could mean wellbore storage while a unit slope at late time is more likely to mean pseudo-steady state flow or boundary dominated flow. Bilinear flow (quarter slope) is typically observed at very early time prior to the onset of linear flow (half slope). The identification and analysis of these flow regimes are crucial for optimizing reservoir management strategies.

You can also aid the interpretation by plotting the data derivative, switching between various time functions available, and using the lasso filter tool on the RNP plot (above the PNR plot) to highlight different sections of the data.

1.9 Solutions of Linear Flow - Surface Oil Rates

Combining constant rate (variable pressure) solution with superposition time allows to account for variable rate solution.

Theoretically, linear flow can be defined in terms of square root of time as follows

For oil: $$\begin{equation} \label{eq:CR-linear-oil} \frac{\Delta p}{q_o}= \frac{p_i-p_{wf}}{q}=\frac{19.927B_{oi}}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_{oi}}{\phi c_{ti}}}\sqrt{t}+b' \end{equation}$$

For gas: $$\begin{equation} \label{eq:CR-linear-gas} \frac{\Delta m(p)}{q_g}=\frac{m(p_i)-m(p_{wf})}{q}=\frac{200.8T_R}{h_fx_f\sqrt{k}}\frac{1}{\sqrt{(\phi\mu_g c_t)_i}}\sqrt{t}+b' \end{equation}$$

For water: $$\begin{equation} \label{eq:CR-linear-water} \frac{\Delta p}{q_w}= \frac{p_i-p_{wf}}{q}=\frac{19.927B_{wi}}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_{wi}}{\phi c_{ti}}}\sqrt{t}+b' \end{equation}$$

For hydrocarbon: $$\begin{equation} \label{eq:CR-linear-hc} \frac{\Delta p}{q_{hc}}= \frac{p_i-p_{wf}}{q}=\frac{19.927}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_{i}}{\phi c_{ti}}}\sqrt{t}+b' \end{equation}$$

For liquid: $$\begin{equation} \label{eq:CR-linear-liq} \frac{\Delta p}{q_{liq}}= \frac{p_i-p_{wf}}{q}=\frac{19.927}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_i}{\phi c_{ti}}}\sqrt{t}+b' \end{equation}$$

For total: $$\begin{equation} \label{eq:CR-linear-total} \frac{\Delta p}{q_{tot}}= \frac{p_i-p_{wf}}{q}=\frac{19.927}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_i}{\phi c_{ti}}}\sqrt{t}+b' \end{equation}$$

Note

For liquid rates, a "pseudo" liquid viscosity is calculated as the saturation weighted average viscosity, as follows $$\begin{equation} \label{eq:visc_pseudo} % 1/psia \mu=\mu_oS_o+\mu_wS_w \end{equation}$$

For total rates, a "pseudo" total viscosity is calculated as the saturation weighted average viscosity, as follows $$\begin{equation} \label{eq:visc_pseudo:tot} % 1/psia \mu=\mu_gS_g+\mu_oS_o+\mu_wS_w \end{equation}$$

in which \(B_o\) is oil formation volume factor in RB/STB, \(B_w\) is water formation volume factor in RB/STB, \(T_R\) is reservoir temperature in rankine, \(\phi\) is porosity in fraction, \(\mu\) is viscosity in cp, \(c_t\) is total compressibility in 1/psia and \(k\) is permeability in md. Fracture height and half-length in feet are denoted by \(h\) and \(x_f\), respectively. Initial and flowing bottomhole pressure are \(p_i\) and \(p_{wf}\) in psia. Water viscosity, \(\mu_w\), is set to 0.5 cp.

Total compressibility accounts for the compressibility of the fluid phases present in the system as well as the rock compressibility and is written as

$$\begin{equation} \label{eq:ct} % 1/psia c_t=c_gS_g+c_oS_o+c_wS_w+c_r \end{equation}$$

where \(c_g\), \(c_o\), \(c_w\) and \(c_r\) denote gas, oil, water and formation (rock) compressibility, respectively. The default value of \(c_r\) is 4x10\(^{-6}\) 1/psia and \(c_w\) is 2.8x10\(^{-6}\) 1/psia in whitson⁺.

\(\Delta m(p)\) is real gas pseudo-pressure drop defined as

$$\begin{equation} \label{eq:Pseudo-Pressure-Drop} % psi2/cp \Delta m(p)=m(p_i)-m(p_{wf})=2\int_{p_{wf}}^{p_i}\frac{p}{\mu_gZ}dp \end{equation}$$

According to Eqs. \eqref{eq:CR-linear-oil}, \eqref{eq:CR-linear-gas}, \eqref{eq:CR-linear-water} the plot of rate normalized pressure \(\left(\frac{\Delta p}{q}\right)\) vs. square root of time \(\sqrt{t}\) (or square root of material balance time \(\sqrt{t_c})\) generates a straight line. The slope of this line is given by

For oil: $$\begin{equation} \label{eq:CR-m-oil} m_{CR}=\frac{19.927B_o}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_o}{\phi c_t}} \end{equation}$$

For gas: $$\begin{equation} \label{eq:CR-m-gas} m_{CR}=\frac{200.8T_R}{h_fx_f\sqrt{k}}\frac{1}{\sqrt{(\phi\mu_g c_t)_i}} \end{equation}$$

For water: $$\begin{equation} \label{eq:CR-m-water} m_{CR}=\frac{19.927B_w}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_w}{\phi c_t}} \end{equation}$$

For hydrocarbon, liquid and total: $$\begin{equation} \label{eq:CR-m-total} m_{CR}=\frac{19.927}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu}{\phi c_t}} \end{equation}$$

Subscript \(CR\) is to emphasize the variable of constant rate solution.

1.10 Skin and Fracture Conductivity

The intercept (\(b'\)) from the linear flow equation is a result of near well effects, e.g. skin \((s')\) and finite fracture conductivity \((F'_{cd})\). The unit of the intercept is psia/STB/d.

Skin and fracture conductivity are defined as follows:

For oil: $$\begin{equation} \label{eq:s-oil} s'=\frac{b'k\left(2x_fn_f\right)}{141.2B_o\mu_o} \end{equation}$$

$$\begin{equation} \label{eq:Fcd-oil} F'_{cd}=\frac{141.2B_o\mu_o}{b'k\ h\ n_f}\times\left(1+\frac{h}{x_f}\left[ln \left\{\frac{h}{2r_w}\right\}-\frac{\pi}{2} \right]\right) \end{equation}$$

For gas: $$\begin{equation} \label{eq:s-gas} s'=\frac{b'k\left(2x_fn_f\right)}{1.417\times 10^6 T_R} \end{equation}$$

$$\begin{equation} \label{eq:Fcd-gas} F'_{cd}=\frac{1.417\times 10^6 T_R}{b'k\ h\ n_f}\times\left(1+\frac{h}{x_f}\left[ln \left\{\frac{h}{2r_w}\right\}-\frac{\pi}{2} \right]\right) \end{equation}$$

For water: $$\begin{equation} \label{eq:s-water} s'=\frac{b'k\left(2x_fn_f\right)}{141.2B_w\mu_w} \end{equation}$$

$$\begin{equation} \label{eq:Fcd-water} F'_{cd}=\frac{141.2B_w\mu_w}{b'k\ h\ n_f}\times\left(1+\frac{h}{x_f}\left[ln \left\{\frac{h}{2r_w}\right\}-\frac{\pi}{2} \right]\right) \end{equation}$$

For hydrocarbon, liquid and total: $$\begin{equation} \label{eq:s-total} s'=\frac{b'k\left(2x_fn_f\right)}{141.2\mu} \end{equation}$$

$$\begin{equation} \label{eq:Fcd-total} F'_{cd}=\frac{141.2\mu}{b'k\ h\ n_f}\times\left(1+\frac{h}{x_f}\left[ln \left\{\frac{h}{2r_w}\right\}-\frac{\pi}{2} \right]\right) \end{equation}$$

Where \(r_w\) (equal 1 ft) indicates well radius in ft and \(n_f\) represents effective fractures number.

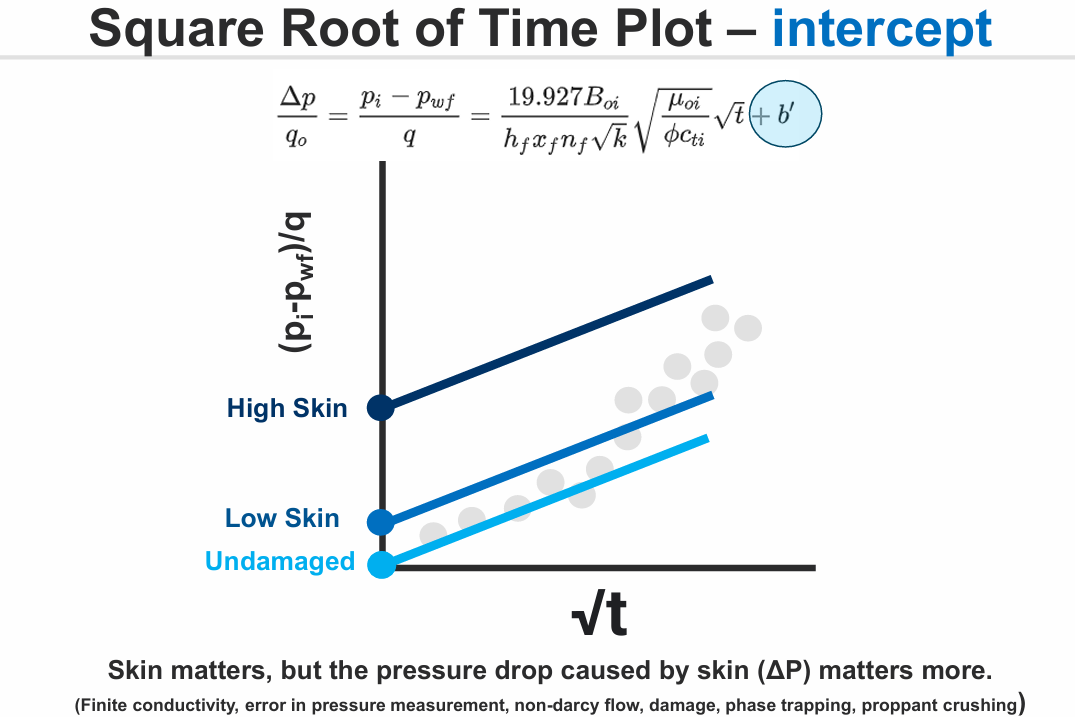
1.11 Linear Flow Parameter

The linear flow parameter (LFP) is expressed in terms of slope of the straight line as

For oil: $$\begin{equation} \label{eq:LFP-oil} % Flow capacity or LFP (ft2md1/2) LFP = A√k = 4\cdot\frac{19.927B_o}{m_{CR}}\sqrt{\frac{\mu_{oi}}{\phi c_{ti}}} \end{equation}$$

For gas: $$\begin{equation} \label{eq:LFP-gas} % Flow capacity or LFP (ft2md1/2) LFP = A√k = 4\cdot\frac{200.8T_R}{m_{CR}}\sqrt{\frac{1}{\left(\phi\mu c_t\right)_i}} \end{equation}$$

For water: $$\begin{equation} \label{eq:LFP-water} % Flow capacity or LFP (ft2md1/2) LFP = A√k = 4\cdot\frac{19.927B_w}{m_{CR}}\sqrt{\frac{\mu_{wi}}{\phi c_{ti}}} \end{equation}$$

For hydrocarbon, liquid and total: $$\begin{equation} \label{eq:LFP-liq-tot} % Flow capacity or LFP (ft2md1/2) LFP = A√k = 4\cdot\frac{19.927}{m_{CR}}\sqrt{\frac{\mu_i}{\phi c_{ti}}} \end{equation}$$

The unit of LFP is ft\(^2\)md\(^{\frac{1}{2}}\).

1.12 Distance of Investigation

It is important to be able to establish the end of the linear flow where the slope on the square root of time plot start to depart from being a straight line. The time to end of linear flow \((t_{elf})\) is key to specify the drainage volume, and to resolve estimates of parameters such as \(k\) and \(x_f\).

Generally, distance of investigation \((y_e)\) can be determined by dividing well horizontal length \((L_w)\) with effective fractures number \((n_f)\).

$$\begin{equation} \label{eq:ye-Lw} y_e=\frac{L_w}{2*n_f} \end{equation}$$

The constant rate solution of \(y_e\), or the distance to the outer boundary is decribed as

$$\begin{equation} \label{eq:CR-ye} y_{e}=0.113\sqrt{\frac{kt_{elf}}{\left(\phi\mu c_t\right)_i}} \end{equation}$$

Combining Eqs. \eqref{eq:ye-Lw} and \eqref{eq:CR-ye} gives

$$\begin{equation} \label{eq:CR-ye-2} \frac{L_w}{2*n_f}=0.113\sqrt{\frac{kt_{elf}}{\left(\phi\mu c_t\right)_i}} \end{equation}$$

The time to end of linear flow \((t_{elf})\) can be solved by rearranging Eq. \eqref{eq:CR-ye-2} $$\begin{equation} \label{eq:CR-telf} t_{elf}=\frac{\left(\phi\mu c_t\right)_i}{k}\left(\frac{L_w}{0.226*n_f}\right)^2 \end{equation}$$

In the case of no deviation of production data from straight line, the latest production time should be used as \(t_{elf}\) which will generate the minimum drainage volume.

1.13 Permeability and Fracture Half-length

1.13.1 Permeability

Rearranging Eq. \eqref{eq:CR-ye-2} to get permeability will result in

$$\begin{equation} \label{eq:CR-k} k=\frac{\left(\phi\mu c_t\right)_i}{t_{elf}}\left(\frac{L_w}{0.226*n_f}\right)^2 \end{equation}$$

1.13.2 Fracture half-length

LFP can also be defined as $$\begin{equation} \label{eq:LFP} LFP=A\sqrt{k} \end{equation}$$

in which \(A\) is total effective fracture surface area in ft\(^2\) defined as $$\begin{equation} \label{eq:total-area-to-flow} A=4n_fhx_f \end{equation}$$

After determining LFP and \(k\) previously, \(x_f\) can be calculated straightforward by rearranging Eqs. \eqref{eq:LFP} and \eqref{eq:total-area-to-flow}.

$$\begin{equation} \label{eq:CR-xf} x_f=\frac{LFP}{4n_fh\sqrt{k}} \end{equation}$$

1.14 Contacted Pore Volume, Drainage Area and Hydrocarbons-in-place

Having all the necessary variables, the contacted pore volume in ft\(^3\) can be easily determined by: $$\begin{equation} \label{eq:pv} V_p=2x_fL_wh\phi \end{equation}$$

Drainage area \(A_d\) in acres (1 acre = 43,560 ft\(^2\)) is defined as $$\begin{equation} \label{ad} A_d=2x_fL_w \end{equation}$$

An alternative way to calculate drainage \(A_d\) is

$$\begin{equation} \label{ad2} A_d = \frac{OOIP * B_{oi}}{7758h\phi(1-S_{wi})} \end{equation}$$

In which 7758 is a conversion factor from acre-ft to bbl.

Original hydrocarbons-in-place are calculated using the following relationships:

For oil: $$\begin{equation} \label{eq:OOIP-RO} % STB OOIP=\frac{V_pS_{oi}}{5.615 B_{oi}} \end{equation}$$

$$\begin{equation} \label{eq:OGIP-RO} % scf OGIP=OOIP \cdot R_{si} \end{equation}$$

For gas: $$\begin{equation} \label{eq:OGIP-RG} % scf OGIP=\frac{V_pS_{gi}}{B_{gi}} \end{equation}$$

$$\begin{equation} \label{eq:OOIP-RG} % STB OOIP=OGIP \cdot R_{vi} \end{equation}$$

For water: $$\begin{equation} \label{eq:OWIP-RW} % STB OWIP=\frac{V_pS_{wi}}{5.615 B_{wi}} \end{equation}$$

1.15 Production Forecast

With simple decline curve analysis, the production forecast can be projected. The classic arps hyperbolic decline is written as

$$\begin{equation} \label{eq:arps-dca} q(t)=q_i\left(1+b\ a_it\right)^{-1/b} \end{equation}$$

Flow production rate and nominal decline rate at the start of forecast are depicted by \(q_i\) and \(a_i\), respectively. Flow production rate at time \(t\) is \(q(t)\) while \(b\) is rate exponent. In this module, the production forecast is start at the end of the linear flow \((t_{elf})\), thus the other variables are with respect to \(t_{elf}\).

Production forecast rate is calculated by rewritting Eq. \eqref{eq:arps-dca} $$\begin{equation} \label{eq:arps-dca-rta} q(t)=\frac{q_{elf}}{\left(1+b\ a_{elf}\left[ t-t_{elf}\right]\right)^{1/b}} \end{equation}$$

A more detailed explanation of decline curve analysis can be found here.

1.16 Geomechanical Effects - Pressure-Dependent Permeability

For gas reservoirs, the matrix can be assigned a pressure-dependent permeability on the form

$$\begin{equation} k(p)=k(p_{Ri})k_m(p) \end{equation}$$

where \(k_m(p)\) is a dimensionless permeability multiplier.

$$\begin{equation} k_m(p)=\exp(\gamma_r(p-{p_{Ri}})) \end{equation}$$

and \(\gamma_r\) is a property that be assigned in the frontend. To activate the pressure-dependent permeability, make \(\gamma_r\) a non-zero value.

To incorporate a variation of permeability with pressure into the pseudo-pressure term, the definition of pseudo-pressure is modified as follows

$$\begin{equation} \label{eq:Pseudo-Pressure-Gamma} % psi2/cp m(p)=2\int_{0}^{p}\frac{pk_m(p)}{\mu_gZ}dp \end{equation}$$

Geomechanical effects can also be added in both the matrix and fracture in the numerical model.

1.17 Computing Original Gas in Place with Adsorption

Shale reservoirs possess a remarkable capacity to store methane through a process known as "adsorption." This involves gas molecules adhering to the organic material within the shale, creating a near-liquid state of condensed gas. A useful analogy is to envision a magnet sticking to a metal surface or lint clinging to a sweater, illustrating the concept of adsorption versus absorption, where one substance is trapped inside another like a sponge soaking up water. The adsorption process is reversible due to its reliance on weak attraction forces.

Compared to conventional reservoirs, shale reservoirs can store significantly more gas in the adsorbed state, even when compression is applied at pressures below 1000 psia. Notably, the gas stored in shale is predominantly held in the adsorbed state, as opposed to being free gas. This is because the volume of the cleat or fracture system within shale is relatively small compared to the overall reservoir volume. As a result, the pressure volume relationship is commonly described through the desorption isotherm alone.

Langmuir Isotherm

The release of adsorbed gas is commonly described by a pressure relationship called the Langmuir isotherm. The Langmuir adsorption isotherm assumes that the gas attaches to the surface of the shale, and covers the surface as a single layer of gas (a monolayer). At low pressures, this dense state allows greater volumes to be stored by sorption than is possible by compression.

The typical formulation of the Langmuir isotherm is:

$$\begin{equation} \label{eq:langmuir} c_g = \frac{V_{LS}p}{p_{LS}+p} \end{equation}$$

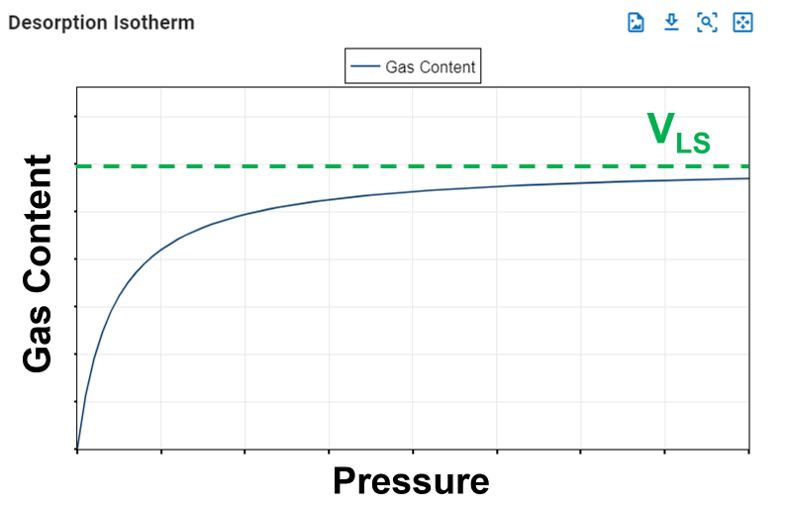
Langmuir Volume, V_LS

The Langmuir volume is the maximum amount of gas that can be adsorbed by a shale at a "infinite pressure". The plot below of a Langmuir isotherm demonstrates that gas content asymptotically approaches the Langmuir volume as pressure increases to infinity.

Fig. 1: Langmuir Volume

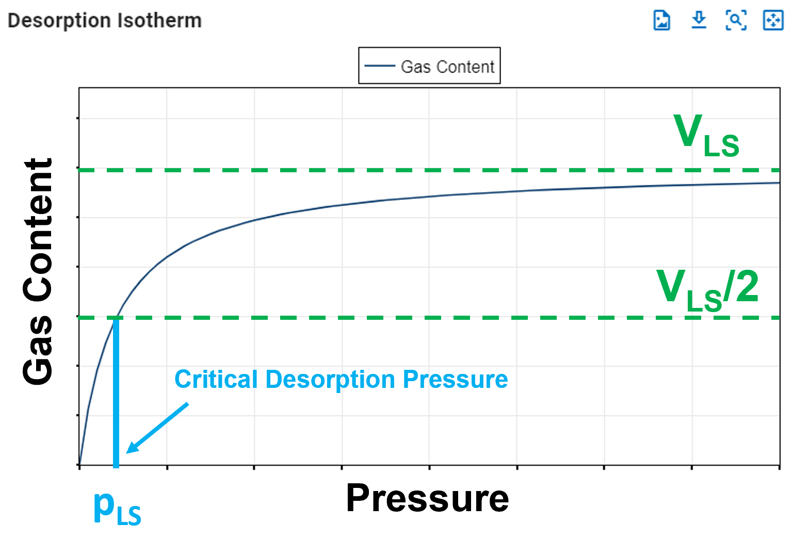
Langmuir Pressure, p_LS

The Langmuir pressure, or critical desorption pressure, is the pressure at which one half of the Langmuir volume can be adsorbed. As seen in the figure below, it changes the curvature of the line and thus affects the shape of the isotherm.

Fig. 2: Langmuir Pressure

Computing Original Gas in Place (OGIP)

Ambrose et al.[1] argue that the free (OGIP) must be corrected for the adsorbed gas that occupies some of the hydrocarbon pore volume (HCPV). If porosity is estimated from core plugs where core preparation has removed the adsorbed gas, then the OGIP will be overestimated.

The convention of reporting OGIP when adsorption is included, is to report it in units of scf/ton (standard cubic feet per short ton). For a fluid system having only dry/wet gas and water, the total OGIP is

$$\begin{equation} \hat{G}=\hat{G}_{f} + \hat{G}_a \end{equation}$$ where

$$\begin{align} \label{eq:freegasperton} \hat{G}_f &= C_1 \frac{\phi(1-S_{wi})-\phi_a}{\rho_bB_{gd}}\\ \label{eq:adsorbedgasperton} \hat{G}_a &= V_{SL} \frac{p}{p+p_{SL}} \end{align}$$ and $$\begin{equation} \phi_a = C_2 M_g \frac{\rho_b}{\rho_s}\bigg(V_{LS}\frac{p}{p+p_{LS}}\bigg) \end{equation}$$ with \(C_1\approx 5.7060\) and \(C_2\approx1.318\cdot10^{-6}\) are unit conversion factors. The shale saturation is capped at \(1-S_{wi}\), meaning the maximum amount of shale you can have is the entire HCPV. Hence, this will make the results independent of the adsorption numbers when violating this constraint.

The OGIP resolved in the ARTA and GFMB features yields the free OGIP. We can use this volume to compute the rock mass, which in turn can be used to calculate the adsorbed OGIP. Multiplying equation \eqref{eq:freegasperton} with the rock mass (\(G=\hat{G}_f m_r\)) gives the free OGIP in units of scf. Solving for the rock mass yields

$$\begin{equation} m_r = \frac{G_f}{C_1} \frac{\rho_b B_{gd}}{\phi(1-S_w)-\phi_a} \end{equation}$$

This rock mass can then be multiplied by equation \eqref{eq:adsorbedgasperton} to get the adsorbed OGIP in scf, i.e., $$\begin{equation} G_a =\hat{G}_a m_r = V_{SL} \frac{p}{p+p_{SL}} m_r \end{equation}$$

Total Compressibility when Adsorption is ON

In order to honor mass balance, it becomes necessary to modify total system compressibility when accounting for adsorption. Total system compressibility can be determined using the following equation:

$$\begin{equation} c_t = c_r + \left(1-S_{wc}\right)c_g + S_wc_w+\frac{\rho_b\rho_g^{sc}}{2000\phi\rho_{ga}}\frac{V_Lp}{p+p_L}\left[\left(\frac{62.428\rho_{ga}}{1000\rho_g^{sc}}B_g-1\right) \left(c_r+\frac{p_L}{p\left(p+p_L\right)}\right)-c_g\right] \end{equation}$$

The derivation of this equation is shown here and is contructed upon Ambrose et al.[1].

1.18 Limitations of Classical RTA

One of the key limitations of classical RTA is the single-phase flow assumption. This is a good assumption for dry and wet gas reservoirs, and when producing with flowing pressures above the saturation pressure. However, for wells producing below the saturation pressure, the single-phase flow assumption is not valid. Hence, using the classical RTA equations for wells subject to multiphase flow effects might skew the interpretation. If the saturation pressure coincides with the change of slope on the square root of time plot, as seen in Fig.2, the slope change might just be an artifact of multiphase flow. To account for the multiphase flow effects, we recommend using the numerical RTA workflow. More info can be found here.

Fig. 2: Slope change coinciding with well dropping below the saturation pressure might be an artifact of multiphase flow.

2. Empirical Assumptions - EUR

The empirical assumptions are used after the time to end liner flow (\(t_{elf}\)) in this feature, and is simply fitting an Arps equation through the historical data after \(t_{elf}\).

The EUR reporting option is available only when using the real-time setting, as forecasting should be performed in real time to ensure accuracy. This approach avoids inconsistencies, such as differences in b-factor handling between real-time and material balance time. For example, the b-factor for BDF is set to 1 (harmonic) in material balance time, while it is 0 (exponential) in real time.

3. Comments on Use of Material Balance Time

• If the analytical solutions are plotted to fully-penetrating fracture problem for either a constant rate or constant pressure case (Eqs. 2 and 3 in Wattenbarger et al. (1998)), a half-slope on a log-log plot should be expected during infinite acting (IA) period with a constant difference between the two solutions of a factor \(\frac{\pi}{2}\). The constant pressure solution in the boundary-dominated flow (BDF) period will exhibit an exponential function, whereas the constant rate solution in the BDF will exhibit a unit-slope.

• If one plots the constant pressure solution versus material balance time, then the curve will (1) overlap the constant rate solution in the BDF period (because material balance time applies rigorously in the BDF period) and, (2) approximate the constant rate solution in the IA period (i.e. it plots close to the true solution, but not on top of it as in the BDF period).

• Because the material balance time solution is only an approximate solution in the IA period, the resulting key numbers (e.g. \(x_f\) and \(k\)) will not be the exact numbers you expect, at least for simple synthetic cases (e.g. a low GOR oil with constant \(p_{wf}\)). However, for a variable rate and pressure solution (real life), one can only get the true values by rigorous superposition (or de-superposition), and thus an approximate solution by the use of material balance time is likely good enough.

4. Constant Flowing Pressure Solution

The constant flowing pressure solution is the opposite of constant rate solution. Instead of having constant rate, it employs variable rate while \(p_{wf}\) is assumed constant.

The workflow of classical RTA is the same for both solutions, the only difference is the equations being used in the calculations. It is worth to mention that there is a factor of \(\pi/2\) difference between the constant rate and constant pressure solutions.

The following equations are applied for contant pressure solution:

4.1 Linear Flow

For oil: $$\begin{equation} \label{eq:CP-linear-oil} \frac{\Delta p}{q_o}= \frac{p_i-p_{wf}}{q}=\frac{31.3B_o}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_o}{\phi c_t}}\sqrt{t}+b' \end{equation}$$

For gas: $$\begin{equation} \label{eq:CP-linear-gas} \frac{\Delta m(p)}{q_g}=\frac{m(p_i)-m(p_{wf})}{q}=\frac{315.4T_R}{h_fx_f\sqrt{k}}\frac{1}{\sqrt{(\phi\mu_g c_t)_i}}\sqrt{t}+b' \end{equation}$$

For water: $$\begin{equation} \label{eq:CP-linear-water} \frac{\Delta p}{q_w}= \frac{p_i-p_{wf}}{q}=\frac{31.3B_w}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_w}{\phi c_t}}\sqrt{t}+b' \end{equation}$$

For hydrocarbon: $$\begin{equation} \label{eq:CR-linear-hc-const-p} \frac{\Delta p}{q_{hc}}= \frac{p_i-p_{wf}}{q}=\frac{31.3}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu}{\phi c_t}}\sqrt{t}+b' \end{equation}$$

For liquid: $$\begin{equation} \label{eq:CR-linear-liq-const-p} \frac{\Delta p}{q_{liq}}= \frac{p_i-p_{wf}}{q}=\frac{31.3}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu}{\phi c_t}}\sqrt{t}+b' \end{equation}$$

For total: $$\begin{equation} \label{eq:CR-linear-total-const-p} \frac{\Delta p}{q_{tot}}= \frac{p_i-p_{wf}}{q}=\frac{31.3}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu}{\phi c_t}}\sqrt{t}+b' \end{equation}$$

4.2 Slope of straight line

For oil: $$\begin{equation} \label{eq:CP-m-oil} m_{CP}=\frac{31.3B_o}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_o}{\phi c_t}} \end{equation}$$

For gas: $$\begin{equation} \label{eq:CP-m-gas} m_{CP}=\frac{315.4T_R}{h_fx_f\sqrt{k}}\frac{1}{\sqrt{(\phi\mu_g c_t)_i}} \end{equation}$$

For water: $$\begin{equation} \label{eq:CP-m-water} m_{CP}=\frac{31.3B_w}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu_w}{\phi c_t}} \end{equation}$$

For hydrocarbon, liquid and total: $$\begin{equation} \label{eq:CR-m-total-const-p} m_{CR}=\frac{31.3}{h_fx_f\sqrt{k}}\sqrt{\frac{\mu}{\phi c_t}} \end{equation}$$

4.3 Linear Flow Parameter

For oil: $$\begin{equation} \label{eq:CP-LFP-oil} % Flow capacity or LFP (ft2md1/2) LFP = A√k = 4\cdot\frac{31.3B_o}{m_{CP}}\sqrt{\frac{\mu_o}{\phi c_t}} \end{equation}$$

For gas: $$\begin{equation} \label{eq:CP-LFP-gas} % Flow capacity or LFP (ft2md1/2) LFP = A√k = 4\cdot\frac{315.4T_R}{m_{CP}}\sqrt{\frac{1}{\left(\phi\mu c_t\right)_i}} \end{equation}$$

For water: $$\begin{equation} \label{eq:CP-LFP-water} % Flow capacity or LFP (ft2md1/2) LFP = A√k = 4\cdot\frac{31.3B_w}{m_{CP}}\sqrt{\frac{\mu_w}{\phi c_t}} \end{equation}$$

For hydrocarbon, liquid and total: $$\begin{equation} \label{eq:LFP-liq-tot-const-p} % Flow capacity or LFP (ft2md1/2) LFP = A√k = 4\cdot\frac{31.3}{m_{CR}}\sqrt{\frac{\mu}{\phi c_t}} \end{equation}$$

4.4 Distance of Investigation

$$\begin{equation} \label{eq:CP-ye} y_{e}=0.159\sqrt{\frac{kt_{elf}}{\left(\phi\mu c_t\right)_i}} \end{equation}$$

4.5 Permeability

$$\begin{equation} \label{eq:CP-k} k={\left(\frac{y_e\sqrt{\phi\mu c_t}}{0.159\sqrt{t_{elf}}}\right)}^2 \end{equation}$$

References

[1] Palacio, J.C. and Blasingame, T.A. "Decline Curve Analysis Using Type Curves; Analysis of Gas Well Production Data." Paper Presented at the SPE Rocky Mountain Regional/Low Permeability Reservoirs Symposium, Denver, Colorado, April 12-13.

[2] Wattenbarger, Robert A., El-Banbi, Ahmed H., Villegas, Mauricio E., and J. Bryan Maggard. "Production Analysis of Linear Flow Into Fractured Tight Gas Wells." Paper presented at the SPE Rocky Mountain Regional/Low-Permeability Reservoirs Symposium, Denver, Colorado, April 1998.

[3] Whitson, Curtis Hays, Coll, Carolina , Dahouk, Mohamad Majzoub, and Aleksander Oma Juell. "Shale Reserve Forecasting - Model Consistency and Uncertainty." Paper presented at the SPE Europec featured at 78th EAGE Conference and Exhibition, Vienna, Austria, May 2016.

[4] Samandarli, Orkhan , Valbuena, Ernesto , and Christine Ehlig-Economides. "Production Data Analysis in Unconventional Reservoirs with Rate-Normalized Pressure (RNP): Theory, Methodology, and Applications." Paper presented at the SPE Americas Unconventional Resources Conference, Pittsburgh, Pennsylvania USA, June 2012.

[5] Ray J. Ambrose, Robert C. Hartman, Yucel Akkutlu, Multi-Component Sorbed-Phase Considerations for Shale Gas-In-Place Calculations, SPE-141416, Society of Petroluem Engineers 2011

[6] Chu, W.–C.. –C., Pandya, N. D., Flumerfelt, R. W., and C.. Chen. "Rate-Transient Analysis Based on the Power-Law Behavior for Permian Wells." SPE Res Eval & Eng 22 (2019): 1360–1370.