DFIT - Diagnostic Fracture Injection Tests
1. What is a DFIT and what can we get from it?
A diagnostic fracture injection test (DFIT), a term coined by Halliburton by Craig and Brown, 1999, is a small-volume, clear water injection test designed to create a hydraulic fracture. After shut-in, the pressure is monitored to estimate:
- Minimum principal stress \((S_{h,min})\)
- Pore pressure
- Permeability\((k)\), and leakoff coefficient \((C_{L})\) – Estimated if the first two above have at least adequate estimates.
Key – Estimation of the Leak-off Coefficient from measured changes in pressure after injection is stopped.
More specifically, this document outlines the procedures laid out in URTeC-2019-123 which is inspired from proven classical fracture compliance modelling, an industry collaboration with field DFIT studies, statistical comparison with full-physics multiphase simulators, after the drawbacks of the ‘holistic’ DFIT procedure using the ‘tangent’ method of interpretation outlined by Barree et al., 2009. This process utilizes classical concepts of stress estimation and fracture compliance methods to prevent underestimating in-situ stress, overestimating permeability and hence improve the well spacing and overall NPV of the field.
DFITs may be conducted for high permeability and low permeability reservoirs where the fracture injection transients behave differently. There is also a difference between horizontal well and vertical well DFIT interpretation where the horizontal wells in shale present new physics and challenges like near-wellbore tortuosity.
2. Operational Procedure - from Cramer and Nguyen, 2013
- Surface pump establishes an injection rate with water and the wellbore fluid is compressed; In low permeability reservoirs, little (if any) of the injection fluid flows into the reservoir during this time.
- Eventually injection pressure exceeds formation breakdown or breakover pressure. Hydraulic fracturing is being propagated into the reservoir rock.
- Water injection at the surface is continued until the wellhead pressure stabilizes.
- Surface injection is stopped, resulting in an Instantaneous shut-in pressure (ISIP) which is net of wellbore and near-wellbore friction pressure. Net pressure at shut-in is determined as sand-face pressure – fracture closure pressure.
- Shut-in well pressure is monitored for signs of fracture closure (indicating the minimum principal stress)
- After-closure period is evaluated for pseudo-linear and pseudo-radial flow signatures to determine initial reservoir pressure and even transmissibility.
3. Important Equations and Assumptions
3.1. The G function (and g function):
Assuming validity of Carter leakoff concepts derived for fluid leakoff through the fracture when the pressure is in the fracture is constant, we can get the G function or the g function as modified time functions to interpret DFITs.
Carter leakoff is valid during injection and slightly after shut-in but not long after when the pressure drop fall off is significant.
The g-function is proportional to the cumulative volume of fluid leaked off from the beginning of injection.
The G function is proportional to the cumulative volume of fluid leaked off after shut-in.
Hence, they are calculated from Carter leakoff equations can be related to each other as well -
where \(\Delta t\) is shut-in duration, and \(t_{e}\) is the duration of injection.
Disadvantages of using G function –
1. It relies on a single ‘point-in-time’ estimate of the dP/dG for estimation of effective permeability. That pick of dP/dG might still be elevated due to residual near-wellbore tortuosity.
2. Relies on Carter leakoff which may not hold perfectly true after shut-in, since the fluid pressure decreases over time.
3.2. The H function (and h function):
Constructed in the same spirit as the G/g function plots to represent the fluid leakoff from the system from the beginning of injection and after shut in.
Time convolutional integral accounts for the deviation from Carter leakoff combining Mayerhofer et al., 1995 and Valko and Economides, 1999 and wellbore storage.
This allows the calculation of leakoff volume down to lower pressures than the G-function approach (tackling the inapplicability of the G function methods during pressure falloff as Carter leakoff becomes invalid).
3.3. Mass balance equations for DFIT:
Provides an additional constraint to be used with G or H function methods for characterization using DFITs.
General Mass balance philosophy for DFITs -
Hence,
where \(C_{w}\) is wellbore storage coefficient, and \(C_{L}\) is the leakoff coefficient.
Fracture stiffness and area are given by \(S_{f}\) and \(A\) respectively and the volume of fluid injected is given by \(V_{inj}\).
This simplification is valid during the ideal Nolte part of the preclosure transient. Thus, only apply the equation during a period that follows the ideal behaviour.
4. What do we need for a DFIT analysis?
Fundamental data collected from the field instrumentation -
- The Pressure data: During the sufficiently long shut in, right after injection is stopped.
- The Rate data: The injection rate and cumulative volume prior to the shut-in.
We use the following plots to generate estimates of the leakoff coefficient and permeability -
- Log-Log plot of P and dP/dG with respect to the G function - stress and pore pressure.
- Log-Log plot of P and dP/dt with respect to the time - identification of impulse flow signatures and post closure transients.
We may use additional plots such as –
- Pressure vs time inverse or square root of time inverse – for extrapolating to pore pressure.
- Relative stiffness plot – calculated from the data and h function to get the contact pressure at closure when data does not follow Carter leakoff. When the relative stiffness increases, it indicates that the fracture walls have come into contact.
5. Typical Signatures
Typical DFIT test in a low permeability reservoir may have the following sections –
- Near-wellbore tortuosity and frictional pressure drop.
- Minimum dP/dG
- Ideal Nolte period (Pre-closure transient) – Pressure in the fractures assumed constant.
- Fracture closure signature, approximately 90% fluid leakoff at peak dP/dG
- Post-closure transients
Fig. 1: Typical DFIT Interpretation
Good G function plot –
Typically considered good quality data if the dP/dG shows an ‘S’ shaped curve with amount of time in constant fracture pressure for a good estimate of minimum principle stress and effective ISIP.
Fig. 2: Examples of good G function plots from DFIT data
Adequate G function plots –
Typically show a very subdued ‘S’ shape with a small difference in minimum and maximum dP/dG since multiple phenomena may be overlapping in time such as near wellbore tortuosity weakening the apparent closure response, making dP/dG almost monotonic but not really.
Fig. 2: Examples of 'adequate' G function plots from DFIT data
Bad G function plots –
This may be due to severe wellbore tortuosity (horizontal wells), rapid closure due to high system permeability, leakoff into pre-existing fractures or an operational problem such as leaks. The G function looks monotonic and cannot be used for estimating anything.
Fig. 3: Examples of 'bad' G function plots from DFIT data - Cannot be used
Vertical vs Horizontal wells –
Notice the early time pressure drop. This is usually higher for horizontal wells than vertical wells since this drop is a function of wellbore frictional pressure drop. Near-wellbore tortuosity promotes a steeper drop. This is why Instantaneous shut-in pressure (ISIP) at pump off may be much higher than the effective ISIP which can be calculated as shown below.
Fig. 4: Examples of G function plots for Horizontal vs Vertical DFITs
6. Estimating Stress, Pore Pressure, and Permeability from Closure and Post-Closure Analysis
Estimating pore pressure and permeability depends on prior data interpretations. The table below links combinations of closure and post-closure interpretations (columns 1–2) to recommended methods for estimating stress, pore pressure, and permeability (columns 3–5). These procedures follow McClure et al. (2019, 2022).
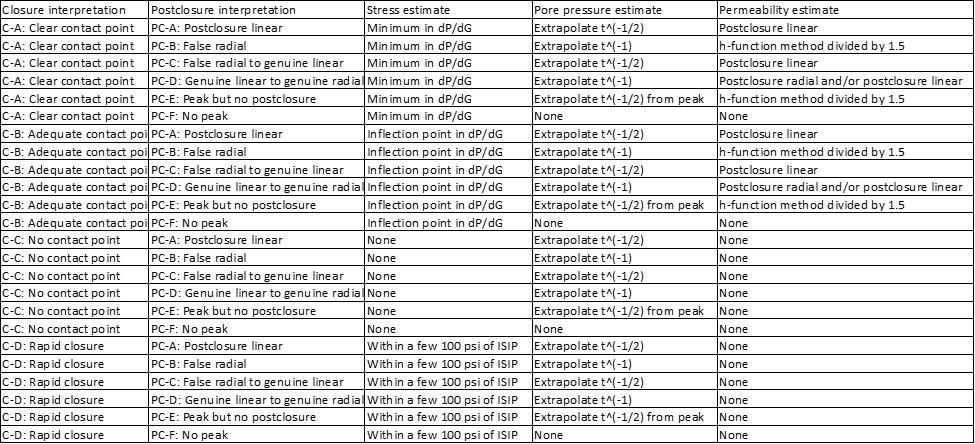
For a detailed explanation of practical guidelines for DFIT interpretation using the ‘compliance method,’ refer to this blog here.
7. Workflow for estimation of Stress
- Plot P and dP/dG vs G function time on a linear plot.
- A good estimate of stress would have the ideal ‘S’ shape in dP/dG. An adequate estimate would have at least a non-monotonic dP/dG with at least a reasonable difference in the minimum and maximum dP/dG. No estimation can be performed if the curve is monotonic.
- Look for the minimum in dP/dG in the dip following the shut in. This should be the ideal Nolte period, with pressure roughly constant. We are in the period where the effect of wellbore tortuosity in pressure leakoff has decayed and the fractures are fully open, i.e. no closure response yet, indicated by the increase in dP/dG from this minimum.
- Add 10% to this minimum dP/dG and get the corresponding Pressure at this dP/dG. This is the contact pressure or pressure at which 90 percent of the fractures can be assumed to be closed.
- Contact pressure is heuristically 75 psi higher than the minimum principle stress, Sh,min. Hence get Sh,min from the Contact Pressure by subtracting 75 psi with an uncertainty of up to 100 psi. This accounts for the remaining ‘stress shadow’ caused by the residual aperture at contact caused by the fracture roughness.
- Get effective ISIP by extrapolating the linear trend found in the ideal Nolte period by extrapolating the trend backward on the same plot to get the y-intercept as effective ISIP, \(P_{ISIP, eff}\).
Fig. 5: Estimating Stress from DFIT data
8. Workflow for estimation of Pore Pressure
- Needs sufficient shut in time to see impulse flow signatures i.e. dP/dG has to peak after the minimum and decay exhibiting a signature slope for a good estimate of pore pressure. You can get an adequate estimate if you have shut in data upto the peak of dP/dG by safely extrapolating and assuming a higher tolerance on the pore pressure uncertainty. If you don’t meet at least these criteria, you cannot estimate pore pressure and hence permeability.
- Note: Gas wells may show false radial before true linear and well may suddenly show a drop in dP/dG indicating wellbore in vacuum – in all of these cases you cannot estimate pore pressure.
- Look for late time impulse linear or radial flow signatures in dP/dG indicated by a slope of -1/2 or -1 respectively.
- If there is impulse linear flow, plot P vs square root time inverse for the pressure data in impulse linear flow.
- If there is impulse radial flow, plot P vs square root time inverse for the pressure data in impulse radial flow.
- Extrapolate these pressure plots to t=0 or y-intercept to get pore pressure.
Fig. 6: Estimating Pore Pressure from DFIT data
9. Workflow for estimation of Permeability
- Use the G function plot, dP/dG to estimate the minimum principal stress and effective ISIP as shown above. This needs to be at least adequate to proceed.
- Search the log-log plot of P vs time for late time impulse flow signatures (most common and reliable is the impulse linear flow with a -1/2 slope on the derivate curve, radial signatures may exist but may be unreliable). Extrapolate from the peak if data is missing for an adequate estimate of pore pressure.
- Choose whether to use preclosure or postclosure estimates of permeability – Post closure methods might be more accurate since they need a clean and reliable impulse flow signature at late time unaffected by multiphase leakoff. Some wells may never have enough shut-in time to show a post closure transient.
9.1. Preclosure Methods
9.1.1. Using the G function
Calculate leakoff Coefficient by making an assumption about fracture geometry as -
For Radial Fractures :-
For PKN (fixed height) Fractures :-
Evaluate these at the minimum dP/dG.
The unknown parameters of fracture geometry in the above, i.e. Rf or Lf, can be determined by writing a mass balance equation for the entire system and evaluating it at effective ISIP and radial fractures, we get –
2 equations and 2 unknowns, solve both the equations simultaneously to get Fracture radius, \(R_{f}\) and leakoff coefficient \(C_{L}\).
Rf is used to calculate Fracture Area, A, if needed.
Once we have CL, we can calculate k as -
9.1.2. Using the h function
First step is to calculate and plot P and dP/dG vs G function and calculate the h function.
Get the time and pressure at which the G*dP/dG is maximum, we assume here that 90 percent fluid has leaked off from the system.
This will be the \(\Delta t_{peak}\) and \(P_{peak}\) used in the calculations coming up.
Writing a global mass balance with that assumption at \(t= \Delta t_{peak}\), we get –
We can then solve for Area in the global mass balance equation.
We can also write a global mass balance at \(\Delta t = 0 \) using effective ISIP to minimize the effect of uncertainty in Sh,min, which in this case reduces the equation to -
Using the appropriate expressions for Sf and Area, depending on radial or PKN fracture geometry assumption, we can estimate the fracture geometry.
For radial fracture geometry -
For PKN fracture geometry -
Once you get Rf or Lf and hence fracture area, A, we can easily get the permeability from the equations shown above.
9.2. Postclosure Methods
You may have either impulse radial or impulse linear flow signatures in your DFIT post closure transient. This may appear on a log-log pressure vs time plot as a derivative slope of -1 or -0.5 respectively. In that case, we can use this data to estimate permeability using late-time analytical solutions for the appropriate flow.
9.2.1. Using Impulse Radial flow
Late time analytical solution for radial flow with constant injection –
Thus, we can write the impulse radial solution as a derivative of this constant rate solution as –
- Plot Pressure vs \(\Delta t^{-1}\) for the data in impulse radial flow.
- We can get the slope of the line which can be used to calculate \(k\) assuming a fracture height, \(‘h’\). This can be assumed from well logs if payzone section is obvious or if there is strong evidence of height confinement allowing us to fix the height of the fracture.
- If height is not known, assume radial fractures set h equal to 2Rf. Now use the kh from the slope above, but divide that by 2Rf instead to get k using this equation below -
9.2.2. Using Impulse Linear flow
Late time analytical solution for linear flow with constant injection –
We can write the impulse linear solution as a derivative of this constant rate solution, taking wellbore storage into account –
- Plot pressure vs inverse of square root time. Get the \(A\sqrt{k}\) from the slope of the data.
- Once we have \(A\sqrt{k}\), estimate radius or length (Rf or Lf) and hence permeability using equations in the preclosure k estimate – h function method.
10. DFIT Tangent Method
The tangent method is a classical and widely used approach for estimating fracture closure pressure from a DFIT. It is based on analyzing the G-function derivative plot (), which highlights changes in the pressure decline behavior during shut-in.
In this method, a tangent line is drawn to the linear portion of the curve observed after closure, where the pressure decline becomes dominated by formation leak-off and system compressibility. The intersection between this tangent line and the actual curve defines the fracture contact pressure—the pressure at which the fracture surfaces first come into contact and stiffness begins to increase.
Note
This approach is fast, visual, and consistent, making it a popular choice for screening multiple DFITs or when data quality is limited. However, users should be aware of a few important considerations:
1. The tangent method can overestimate closure pressure in cases where fracture stiffness evolves gradually rather than abruptly.
2. The method assumes Carter leak-off and idealized linear fracture behavior, which may not hold in heterogeneous or low-permeability formations.
3. It relies on subjective tangent placement, which introduces interpreter bias.
To adjust the fit line in the DFIT tangent method, hold the end of the line to modify the slope, then move the circle along the line to set the intersection point.
whitson+ includes both the tangent and compliance methods to give users flexibility. While the tangent method remains a useful first-pass diagnostic, the compliance method provides a more physically grounded estimate by directly tracking stiffness evolution with time and pressure. Either method results in an estimate of fracture contact pressure and minimum principal stress - which flows into the subsequent permeability calculations.
Recommendation:
Use the compliance method as the default approach for closure determination. The tangent method is best used for cross-checking results or for quick, visual QC of DFIT behavior across multiple tests.
DFIT Workflow
Before Getting Started
Recommended Data Size for DFIT Tests
DFIT datasets could be far higher frequency than needed. Datasets can vary from second by second frequency to tens of seconds for the entirety of the test. This can be harder to handle, and make the numerical derivative calculation unweildy.
Instead of uploading such high resolution data, the recommended practice is to smooth the dataset externally by resampling the data in terms of pressure increments of 5 to 10 psi. Note that there is a further reduction using pressure increments of 30 psi in the DFIT feature to improve speed for dynamic calculations too. However, it is good practice to limit the number of data rows uploaded into whitson+ to between 30,000 and 40,000. To learn how to resample your data within whitson+, see the resampling section here.
Mass Upload Sheets
Using Mass Upload sheets to get your DFIT data
Add a well name to the Well Data sheet, you do not need to enter anything else in this sheet.
Use the same well name in the Production Data sheet to add DFIT data to the well:
Key information required
Pressure (bottomhole) vs time
- Time can be in Days or DateTime like 'YYYY-MM-DD hh:mm:ss.000'. Smallest resolution is 1 millisecond.
- Pressure (in psia) vs time data. If only wellhead pressure is available, use the hydrostatic head of water at TVD to correct to bottomhole depth.
Enter these in the pwf or Gauge Pressure column. - Injection rate (in STB/d) vs time data (if available). Enter these in the or Water Rate column on the mass upload Production Data sheet.
Additional required information that cannot be uploaded via mass upload template:
Young's modulus, Poisson's ratio, reservoir fluid viscosity and compressibility.
We also need the estimated fracture height for the assumption of PKN fracture geometry.
You can enter all this information in the DFIT feature under 'Physical Assumptions'.
DFIT Dataset Example
Here's an example DFIT dataset formatted to be uploaded via the standard mass upload template:
Example DFIT Dataset
Courtesy: MCclure et. al, Resfrac
Choices/Assumptions That Need to be Made:
- Choose the preclosure method of choice (G-function and H-function with Radial and PKN fractures) - recommended to go with H-function method with radial fracture geometry.
- Choose the postclosure method of choice based on late time impulse flow signatures (linear/radial flow). Note that the preclosure assumption on fracture geometry also auto-applies to the post closure analysis.
Some notes on automated selections in the software
These preliminary steps are done automatically, you may still need to review these selections -
- Shut in is detected automatically from zero rate. Instantaneous ISIP is identified as the pressure right after the well is shut in.
- Initial pressure, Pw,init is chosen as the first point in the pressure data.
- Cumulative injection volume, and maximum sustained injection rate until the shut in time (characteristic rate), is calculated from the plot. Injection duration is autocomputed from the two above.
- Slope in the pressure vs cumulative injection (Wellbore Storage plot) is detected to calculate the wellbore storage. If rate data is unavailable, just enter the values cumulative injected volume, maximum sustained rate, and wellbore storage.
- Pore pressure is calculated automatically by extrapolating the post closure linear transient (default) on the inverse square root time plot.
Create a Project
- Go to the Projects module in the navigation panel.
- Click ADD PROJECT up to the right.
- Name the project "your name - DFIT Example Certificate".
- Click SAVE.
- Click MASS UPLOAD up to the right.
- Upload the DFIT Example WellOne Excel file.
- Click SAVE.
- All steps are shown in the .gif above.
Navigate to the DFIT feature under the Well Testing section.
Parameters
- Go to the DFIT section in the Well Testing module in the navigation panel.
- Review the automatic selection of parameters from the plots, i.e. Literal ISIP, initial pressure, injected volume, characteristic rate, wellbore storage coefficient, minimum .
- Enter the additional parameters relevant for the calculation, i.e. Young's modulus, Poisson's ratio, reservoir fluid viscosity and compressibility.
Physical Assumptions
Dropdowns for preclosure method and post closure methods allow you to switch between the different methods as well as fracture geometry assumption.
- Selection of frac geometry (Radial/PKN) in preclosure methods enforces the same geometry assumption in postclosure methods.
Note that PKN fractures will need fracture height as an additional input.
G-Function Plot
- Identify point of minimum in the G-Function plot.
- Identify point of maximum.
- All steps are shown in the .gif above.
This automatically computes the effective ISIP, Fracture Contact Pressure and Minimum Principal Stress and are used in subsequent calculations for permeability. The resolved values could be overwritten.
Late Time Shut-In Identification
- Click the slash icon to the top right in the dp after shut-in plot to add a slope.
- Identify if the late time shut in data has post closure transients
- Linear flow will have a half-slope signature and radial flow (rare, beware of false radial signatures in gas wells) will have a unit slope signature.
- Add the interpretation lines if needed and switch the plot (to the right) to impulse radial flow plot by clicking the 'plot radial' button.
- Align the slope to the pressure points near x=0 and let that extrapolate to calculate the pore pressure.
- All steps are shown in the .gif above.
Permeability Computation
Calculation should dynamically run when any of the inputs are changed to compute permeability. If you have reliable post closure transients, use the permeability estimates from the postclosure analysis. Correct preclosure permeability estimates by about 1.5 since they statistically tend to overestimate the permeability.
Additional Resources
*Keep checking this section for more updates.
Reach out to support@whitson.com for any questions or additional information, and demos!
References
[3] DFIT Interpretation, The URTeC-2019-123 Procedure on SAGA Wisdom - Taught by Mark McClure